जनसंख्या का मतलब है

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि सांख्यिकी में जनसंख्या का क्या अर्थ है। इसी तरह, आपको पता चलेगा कि जनसंख्या माध्य का सूत्र क्या है, जनसंख्या माध्य के विश्वास अंतराल की गणना कैसे की जाती है और, इसके अलावा, जनसंख्या माध्य और ‘नमूने’ के माध्य के बीच क्या अंतर है।

जनसंख्या का औसत क्या है?

जनसंख्या माध्य सांख्यिकीय जनसंख्या के सभी तत्वों का अंकगणितीय औसत है। इसलिए, जनसंख्या माध्य की गणना करने के लिए, सभी जनसंख्या मूल्यों को जोड़ा जाना चाहिए और फिर जनसंख्या में तत्वों की कुल संख्या से विभाजित किया जाना चाहिए।

जनसंख्या माध्य का प्रतीक ग्रीक अक्षर μ है।

इसी प्रकार, जनसंख्या माध्य को उस चर के अपेक्षित मान के रूप में भी परिभाषित किया जा सकता है जो जनसंख्या का प्रतिनिधित्व करता है।

जनसंख्या औसत की गणना कैसे करें

एक बार जब हमने जनसंख्या माध्य की परिभाषा देख ली, तो आइए देखें कि इसके अर्थ को बेहतर ढंग से समझने के लिए जनसंख्या माध्य की गणना कैसे की जाती है।

यदि सांख्यिकीय जनसंख्या में सभी मान ज्ञात हैं, तो जनसंख्या माध्य की गणना के लिए अंकगणित माध्य सूत्र को आसानी से लागू किया जाना चाहिए। तो इस मामले में, जनसंख्या माध्य की गणना करने के लिए, हमें सभी जनसंख्या मूल्यों को जोड़ना होगा और फिर डेटा की कुल संख्या से विभाजित करना होगा।

इस प्रकार, यदि हम जनसंख्या के सभी तत्वों का मान जानते हैं, तो जनसंख्या माध्य की गणना करने का सूत्र इस प्रकार है:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ देखें: अंकगणितीय माध्य की गणना का उदाहरण

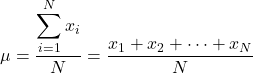
हालाँकि, सामान्य तौर पर सभी जनसंख्या मान ज्ञात नहीं होते हैं, इसलिए सामान्यतः जनसंख्या माध्य का मान अंतरालों द्वारा अनुमानित किया जाता है ।

जनसंख्या माध्य के लिए विश्वास अंतराल

व्यवहार में, किसी जनसंख्या में सभी व्यक्तियों का अध्ययन करना असंभव है, इसलिए आम तौर पर जनसंख्या का एक यादृच्छिक नमूना चुना जाता है और, उसके मूल्यों के आधार पर, जनसंख्या माध्य के मूल्य का अनुमान लगाया जाता है। अधिक सटीक रूप से, हम एक अंतराल की गणना करते हैं जिसमें पूरी आबादी का माध्य होने की बहुत संभावना है; इस अंतराल को जनसंख्या माध्य के लिए विश्वास अंतराल कहा जाता है।

जनसंख्या माध्य के लिए विश्वास अंतराल की गणना नमूना माध्य से जोड़कर और घटाकर Z _α/2 के मान को मानक विचलन (σ) से गुणा करके और नमूने की ऊंचाई (n) के वर्गमूल से विभाजित करके की जाती है। इसलिए, जनसंख्या माध्य के लिए विश्वास अंतराल की गणना करने का सूत्र है:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

उपरोक्त सूत्र का उपयोग तब किया जाता है जब जनसंख्या भिन्नता ज्ञात होती है। हालाँकि, यदि जनसंख्या भिन्नता अज्ञात है, जो कि सबसे आम मामला है, तो माध्य के लिए विश्वास अंतराल की गणना निम्नलिखित सूत्र का उपयोग करके की जाती है:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

सोना:

$\overline{x}$

नमूना साधन है.
$t_{\alpha/2}$

प्रायिकता α/2 के साथ स्वतंत्रता की n-1 डिग्री के छात्र के t वितरण का मान है। बड़े नमूना आकार और 95% आत्मविश्वास स्तर के लिए यह आमतौर पर 1.96 के करीब है और 99% आत्मविश्वास स्तर के लिए यह आमतौर पर 2.576 के करीब है।
$s$

नमूना मानक विचलन है.
$n$

नमूना आकार है.

➤ देखें: जनसंख्या माध्य के लिए विश्वास अंतराल की गणना का उदाहरण

जनसंख्या माध्य और नमूना माध्य

अंत में, संक्षेप में, हम जनसंख्या माध्य और नमूना माध्य के बीच अंतर की समीक्षा करेंगे ताकि ये दो सांख्यिकीय अवधारणाएँ स्पष्ट हों।

जनसंख्या माध्य और नमूना माध्य के बीच का अंतर मूल्यों की वह सीमा है जिस पर माध्य की गणना की जाती है। जनसंख्या माध्य संपूर्ण सांख्यिकीय जनसंख्या का औसत है, जबकि नमूना माध्य जनसंख्या के नमूने का औसत है।

इसके अतिरिक्त, जनसंख्या माध्य को नमूना माध्य से अलग करने के लिए, उन्हें विभिन्न प्रतीकों द्वारा दर्शाया जाता है। जनसंख्या साधन का प्रतीक है

$\mu$

दूसरी ओर, नमूना साधन का प्रतीक है

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

यदि आपको अभी भी इन दो प्रकार के औसतों के बीच अंतर के बारे में संदेह है या नमूना औसत की गणना के बारे में अधिक जानना चाहते हैं, तो आप निम्नलिखित लेख देख सकते हैं:

➤ देखें: नमूने का मतलब क्या है?

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने