माध्य का नमूना वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि आंकड़ों में माध्य का नमूना वितरण क्या है। आपको माध्य नमूना वितरण सूत्र और चरण दर चरण हल किया गया अभ्यास भी मिलेगा।

माध्य का नमूना वितरण क्या है?

माध्य का नमूना वितरण (या साधनों का नमूना वितरण ) वह वितरण है जो किसी जनसंख्या से प्रत्येक संभावित नमूने के नमूना माध्य की गणना के परिणामस्वरूप होता है। अर्थात्, जनसंख्या के सभी संभावित नमूनों से नमूना माध्य का सेट माध्य का नमूना वितरण बनाता है।

या दूसरे शब्दों में, यदि हम उन सभी नमूनों का अध्ययन करते हैं जो किसी जनसंख्या से लिए जा सकते हैं और प्रत्येक नमूने के औसत की गणना करते हैं, तो परिकलित मानों का सेट नमूना माध्य का एक नमूना वितरण बनाता है।

आंकड़ों में, माध्य के नमूना वितरण का उपयोग एकल नमूने का विश्लेषण करते समय जनसंख्या माध्य के मूल्य के करीब पहुंचने की संभावना की गणना करने के लिए किया जाता है।

माध्य के नमूना वितरण के लिए सूत्र

एक ऐसी जनसंख्या को देखते हुए जो माध्य के साथ सामान्य संभाव्यता वितरण का अनुसरण करती है

$\mu$

और मानक विचलन

$\sigma$

और आकार के नमूने निकाले जाते हैं

$n$

, माध्य का नमूना वितरण भी निम्नलिखित विशेषताओं वाले सामान्य वितरण द्वारा परिभाषित किया जाएगा:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

सोना

$\mu_{\overline{x}}$

माध्य के नमूना वितरण का माध्य है और

$\sigma_{\overline{x}}$

इसका मानक विचलन है. आगे,

$\cfrac{\sigma}{\sqrt{n}}$

नमूना वितरण की मानक त्रुटि है।

नोट: यदि जनसंख्या सामान्य वितरण का पालन नहीं करती है, लेकिन नमूना आकार बड़ा है (n>30), तो माध्य का नमूना वितरण भी केंद्रीय सीमा प्रमेय द्वारा पिछले सामान्य वितरण के बराबर अनुमानित किया जा सकता है।

इसलिए, चूंकि माध्य का नमूना वितरण सामान्य वितरण का अनुसरण करता है, नमूना माध्य से संबंधित किसी भी संभावना की गणना करने का सूत्र है:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

सोना:

$\overline{x}$

नमूना साधन है.
$\mu$

यह जनसंख्या का औसत है.
$s$

जनसंख्या मानक विचलन है.
$n$

नमूना आकार है.
$Z$

मानक सामान्य वितरण N(0,1) द्वारा परिभाषित एक चर है।

माध्य के नमूना वितरण का वास्तविक दुनिया का उदाहरण

माध्य के नमूना वितरण की परिभाषा और इससे जुड़े सूत्र क्या हैं, यह देखने के बाद, आइए अवधारणा को बेहतर ढंग से समझने के लिए एक उदाहरण हल करें।

विश्वविद्यालय के छात्रों का वजन 68 किलोग्राम के औसत और 9 किलोग्राम के मानक विचलन के साथ सामान्य वितरण का पालन करता है। दृढ़ निश्चय वाला:
1. इसकी क्या प्रायिकता है कि 25 विद्यार्थियों के यादृच्छिक नमूने का औसत 66 किग्रा से कम है?
2. यदि प्रत्येक 25 छात्रों के आकार के साथ 300 नमूने लिए जाते हैं, तो कितने नमूनों का औसत मूल्य 66 किलोग्राम से कम होगा?

सबसे पहले, हमें संबंधित आँकड़ों के मूल्य की गणना करनी चाहिए, इसके लिए हम वह सूत्र लागू करते हैं जो हमने ऊपर देखा:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}=\frac{66-68}{\displaystyle\frac{9}{\sqrt{25}}}=-1,11$

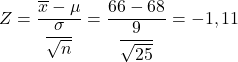
इसलिए हम जिस संभाव्यता की तलाश कर रहे हैं वह मानक सामान्य वितरण की बाईं पूंछ के मान Z=-1.11 के अनुरूप है, जिसे Z संभाव्यता तालिका से आसानी से प्राप्त किया जा सकता है। इसलिए हम इस संभावना को निर्धारित करने के लिए Z तालिका का उपयोग करते हैं कि समस्या हमसे क्या पूछती है:

$P[\overline{x}\leq 66]=P[Z\leq -1,11] =0,1335$

➤ देखें: तालिका Z

अब जब हम संभावना जानते हैं कि एक यादृच्छिक नमूने का माध्य 66 किलोग्राम से कम है, तो यह जानने के लिए कि 300 समान नमूने लेने पर नमूनों की संख्या 66 किलोग्राम से कम है, हमें गणना की गई संभावना को लिए गए नमूनों की कुल संख्या से गुणा करना होगा:

$0,1335\cdot 300 =40,05 \approx 40$

इसलिए, निकाले गए नमूनों में से लगभग 40 का औसत वजन 66 किलोग्राम से कम होगा।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

माध्य का नमूना वितरण क्या है?

माध्य के नमूना वितरण के लिए सूत्र

माध्य के नमूना वितरण का वास्तविक दुनिया का उदाहरण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने