अनुपात का नमूना वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि आंकड़ों में अनुपात का नमूना वितरण क्या है। इसी तरह, आपको अनुपात नमूना वितरण सूत्र और, इसके अलावा, चरण-दर-चरण हल किया गया अभ्यास मिलेगा।

अनुपात का नमूना वितरण क्या है?

अनुपात का नमूना वितरण (या अनुपात का नमूना वितरण ) वह वितरण है जो किसी जनसंख्या से प्रत्येक संभावित नमूने के अनुपात की गणना के परिणामस्वरूप होता है। अर्थात्, किसी जनसंख्या से सभी संभावित नमूनों का नमूना अनुपात, अनुपात का नमूना वितरण बनाता है।

दूसरे शब्दों में, अनुपात का नमूना वितरण उन सभी नमूनों का अध्ययन करके प्राप्त किया जाता है जिन्हें जनसंख्या से चुना जा सकता है और प्रत्येक नमूने का नमूना अनुपात प्राप्त किया जा सकता है। इस प्रकार, गणना किए गए नमूना अनुपातों का सेट अनुपात के नमूना वितरण का गठन करता है।

यदि आप सोच रहे हैं कि अनुपात का नमूना वितरण किस लिए है, तो आंकड़ों में इसका उपयोग एकल नमूने का विश्लेषण करते समय जनसंख्या अनुपात के मूल्य के करीब पहुंचने की संभावना की गणना करने के लिए किया जाता है।

➤ देखें: माध्य का नमूना वितरण

आनुपातिक नमूनाकरण वितरण सूत्र

वास्तव में, जब हम किसी नमूने के अनुपात का अध्ययन करते हैं, तो हम सफलता के मामलों का विश्लेषण करते हैं। इसलिए, अध्ययन में यादृच्छिक चर एक द्विपद संभाव्यता वितरण का अनुसरण करता है।

केंद्रीय सीमा प्रमेय के अनुसार, बड़े आकार (n>30) के लिए हम एक द्विपद वितरण को सामान्य वितरण के करीब ला सकते हैं। इसलिए, अनुपात का नमूना वितरण निम्नलिखित मापदंडों के साथ एक सामान्य वितरण का अनुमान लगाता है:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

सोना

$p$

सफलता की संभावना है और

$q$

विफलता की संभावना है

$q=1-p$

नोट: एक द्विपद वितरण को केवल सामान्य वितरण के समान ही अनुमानित किया जा सकता है यदि

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”> , <p class=$ $np\ge 5$

और

$nq\ge 5$

➤ देखें: सामान्य वितरण के उदाहरण

इसलिए, चूंकि अनुपात के नमूना वितरण को सामान्य वितरण के समान अनुमानित किया जा सकता है, इसलिए नमूने के अनुपात से संबंधित किसी भी संभावना की गणना करने का सूत्र है:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

सोना:

$\widehat{p}$

नमूना अनुपात है.
$p$

जनसंख्या का अनुपात है.
$q$

जनसंख्या की विफलता की संभावना है,

$q=1-p$

.
$n$

नमूना आकार है.
$Z$

मानक सामान्य वितरण N(0,1) द्वारा परिभाषित एक चर है।

आनुपातिक नमूनाकरण वितरण का ठोस उदाहरण

एक बार जब हमने आनुपातिक नमूनाकरण वितरण की परिभाषा देखी और इसके संबंधित सूत्र क्या हैं, तो अवधारणा को पूरी तरह से समझने के लिए चरण दर चरण हल किया गया उदाहरण नीचे दिया गया है।

एक औद्योगिक कंपनी एक कारखाने से भागों के बैच खरीदती है जो केवल 3% दोषपूर्ण भागों के साथ भागों का उत्पादन करने का दावा करती है। इसे जाँचने के लिए, कंपनी 500 भागों के ऑर्डर का विश्लेषण करने का निर्णय लेती है। नमूने में 5% से अधिक दोषपूर्ण हिस्से मिलने की संभावना क्या है?

इस मामले में, जिस जनसंख्या का हम अध्ययन करना चाहते हैं उसका अनुपात 0.03 है, इसलिए पैरामीटर q 0.97 के बराबर है।

$\begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}$

इसलिए, संभावना जानने के लिए कि वे हमसे क्या पूछते हैं, हमें उस सूत्र को लागू करके संबंधित आंकड़ों की गणना करनी चाहिए जो हमने पिछले अनुभाग में देखा था:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}=\cfrac{0,05-0,03}{\displaystyle\sqrt{\frac{0,03\cdot 0,97}{500}}}=2,62$

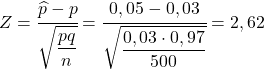
इस प्रकार 5% से अधिक दोषपूर्ण हिस्से प्राप्त होने की संभावना निम्नलिखित संभावना के बराबर है:

$P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”> अंत में, हम <a href=$ Z वितरण तालिका में P[Z≤2.62] की संभावना की तलाश करते हैं और उस संभावना की गणना करते हैं जो समस्या हमसे पूछती है:

$\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”> निष्कर्षतः, विश्लेषण किए गए नमूने में 5% से अधिक दोषपूर्ण हिस्से मिलने की संभावना 0.44% है। </div>  <div class=$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

अनुपात का नमूना वितरण क्या है?

आनुपातिक नमूनाकरण वितरण सूत्र

आनुपातिक नमूनाकरण वितरण का ठोस उदाहरण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने