विद्यार्थी का टी-टेस्ट

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि स्टूडेंट टी टेस्ट क्या है और सांख्यिकी में इसका उपयोग किस लिए किया जाता है। इस प्रकार, आप जानेंगे कि छात्र का टी परीक्षण कैसे किया जाता है, छात्र के टी परीक्षण के विभिन्न प्रकार क्या हैं, और प्रत्येक के लिए सूत्र क्या हैं।

विद्यार्थी का टी-टेस्ट क्या है?

छात्र का टी-टेस्ट , जिसे टी-टेस्ट या बस टी-टेस्ट भी कहा जाता है, एक सांख्यिकीय परीक्षण है जिसमें परीक्षण आँकड़ा छात्र के टी-वितरण का अनुसरण करता है। इसलिए, आंकड़ों में, किसी परिकल्पना परीक्षण की शून्य परिकल्पना को अस्वीकार करने या स्वीकार करने के लिए छात्र के टी-टेस्ट का उपयोग किया जाता है।

विशेष रूप से, छात्र के टी-टेस्ट का उपयोग परिकल्पना परीक्षण में किया जाता है जिसमें अध्ययन की जा रही जनसंख्या सामान्य वितरण का पालन करती है, लेकिन जनसंख्या भिन्नता जानने के लिए नमूना आकार बहुत छोटा है।

संक्षेप में, छात्र के टी-टेस्ट का उपयोग कुछ परिकल्पना परीक्षणों की अध्ययन परिकल्पना को अस्वीकार करने या स्वीकार करने के लिए किया जाता है। उदाहरण के लिए, छात्र के टी-टेस्ट का उपयोग एक नमूने के लिए, स्वतंत्र नमूनों के लिए, या संबंधित नमूनों के लिए परिकल्पनाओं का परीक्षण करने के लिए किया जाता है। फिर हम देखेंगे कि प्रत्येक मामले में छात्र के टी-टेस्ट की गणना कैसे की जाती है।

विद्यार्थियों के टी-परीक्षणों के प्रकार

विद्यार्थियों के परीक्षण तीन प्रकार के होते हैं:

एक-नमूना छात्र का टी-टेस्ट – नमूना माध्य के मूल्य के बारे में परिकल्पना का परीक्षण करने के लिए उपयोग किया जाता है।
दो स्वतंत्र नमूनों के लिए छात्र का टी परीक्षण : यह आपको दो स्वतंत्र नमूनों के बीच के अंतर पर परिकल्पना का परीक्षण करने की अनुमति देता है।
दो युग्मित नमूनों (या संबंधित नमूनों) के लिए छात्र का टी-परीक्षण – दो बार परीक्षण किए गए नमूने के माध्य के बारे में परिकल्पना की जांच करने के लिए उपयोग किया जाता है।

विद्यार्थी के टी-टेस्ट का एक नमूना

नमूना माध्य के लिए परिकल्पना परीक्षण वे होते हैं जिनमें शून्य परिकल्पना और परीक्षण की वैकल्पिक परिकल्पना जनसंख्या माध्य के मूल्य के बारे में कुछ कहती है।

एक-नमूना छात्र टी परीक्षण का सूत्र इस प्रकार है:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

सोना:

$t$

माध्य के लिए परिकल्पना परीक्षण आँकड़ा है, जिसे छात्र के टी वितरण द्वारा परिभाषित किया गया है।
$\overline{x}$

नमूना साधन है.
$\mu$

परिकल्पना परीक्षण में प्रस्तावित माध्य का मान है।
$s$

नमूना मानक विचलन है.
$n$

नमूना आकार है.

एक बार छात्र के टी परीक्षण के मूल्य की गणना हो जाने के बाद, महत्वपूर्ण मूल्य के साथ सांख्यिकीय परीक्षण के परिणाम की व्याख्या शून्य परिकल्पना को अस्वीकार करने या न करने के लिए की जानी चाहिए:

यदि माध्य के लिए परिकल्पना परीक्षण दो-तरफा है, तो शून्य परिकल्पना खारिज कर दी जाती है यदि छात्र के टी परीक्षण का पूर्ण मूल्य महत्वपूर्ण मूल्य टी _α/2|n-1 से अधिक है।
यदि माध्य के लिए परिकल्पना परीक्षण सही पूंछ से मेल खाता है, तो शून्य परिकल्पना खारिज कर दी जाती है यदि छात्र का t-परीक्षण मान महत्वपूर्ण मान t _α|n-1 से अधिक है।
यदि माध्य के लिए परिकल्पना परीक्षण बाईं पूंछ से मेल खाता है, तो शून्य परिकल्पना खारिज कर दी जाती है यदि छात्र का टी-परीक्षण मान महत्वपूर्ण मान -t _α|n-1 से कम है।

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

ध्यान दें कि महत्वपूर्ण परीक्षण मान छात्र की वितरण तालिका से प्राप्त किए जाते हैं।

➤ देखें: माध्य के लिए परिकल्पना परीक्षण का ठोस उदाहरण

स्वतंत्र नमूनों के लिए विद्यार्थी का टी परीक्षण

स्वतंत्र नमूनों के लिए छात्र के टी-टेस्ट का उपयोग दो आबादी के साधनों के बीच संबंध की परिकल्पना को अस्वीकार या स्वीकार करने के लिए किया जाता है, उदाहरण के लिए, कि दो आबादी के साधन अलग-अलग हैं या जनसंख्या ए का औसत औसत से अधिक है . जनसंख्या बी.

हालाँकि, इस मामले में, छात्र का टी-टेस्ट फॉर्मूला इस पर निर्भर करता है कि जनसंख्या भिन्नता को बराबर माना जा सकता है या नहीं। फिर हम दो संभावित मामले देखेंगे।

अज्ञात और समान विचलन

जब जनसंख्या भिन्नताएं अज्ञात हैं लेकिन बराबर मानी जाती हैं तो स्वतंत्र नमूनों के लिए छात्र टी परीक्षण की गणना करने का सूत्र इस प्रकार है:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

सोना:

$t$

अज्ञात भिन्नताओं वाले साधनों के अंतर के लिए परिकल्पना परीक्षण आँकड़ा है, जो स्वतंत्रता की n ₁ + n ₂ -2 डिग्री के साथ एक छात्र के t वितरण का अनुसरण करता है।
$\mu_1$

जनसंख्या 1 का माध्य है.
$\mu_2$

जनसंख्या का माध्य है 2.
$\overline{x_1}$

नमूना 1 का माध्य है.
$\overline{x_2}$

नमूना 2 का माध्य है.
$s_p$

एकत्रित मानक विचलन है।
$n_1$

नमूना आकार 1 है.
$n_2$

नमूना आकार 2 है.

दो नमूनों के संयुक्त मानक विचलन की गणना निम्न सूत्र का उपयोग करके की जाती है:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

अज्ञात और विभिन्न विविधताएँ

जब जनसंख्या भिन्नताएं अज्ञात होती हैं और, इसके अलावा, भिन्न मानी जाती हैं, तो स्वतंत्र नमूनों के लिए छात्र के टी परीक्षण की गणना करने का सूत्र इस प्रकार है:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

सोना:

$t$

अज्ञात भिन्नताओं वाले साधनों के अंतर के लिए परिकल्पना परीक्षण आँकड़ा है, जो एक छात्र के टी वितरण का अनुसरण करता है।
$\mu_1$

जनसंख्या 1 का माध्य है.
$\mu_2$

जनसंख्या का माध्य है 2.
$\overline{x_1}$

नमूना 1 का माध्य है.
$\overline{x_2}$

नमूना 2 का माध्य है.
$\sigma_1$

जनसंख्या 1 का मानक विचलन है.
$\sigma_2$

जनसंख्या 2 का मानक विचलन है।
$n_1$

नमूना आकार 1 है.
$n_2$

नमूना आकार 2 है.

हालाँकि, इस मामले में, छात्र के टी वितरण की स्वतंत्रता की डिग्री की गणना निम्नलिखित सूत्र का उपयोग करके की जाती है:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ देखें: साधनों में अंतर के लिए परिकल्पना परीक्षण का ठोस उदाहरण

युग्मित या संबंधित नमूनों के लिए विद्यार्थी का टी परीक्षण

इस परीक्षण का उपयोग तब किया जाता है जब अध्ययन किए जा रहे दो नमूने एक-दूसरे से संबंधित होते हैं, ताकि यह वास्तव में व्यक्तियों का एक ही नमूना हो जिसका दो बार विश्लेषण किया गया हो (हर बार अलग-अलग परिस्थितियों में)।

उदाहरण के लिए, आप गणित और सांख्यिकी पाठ्यक्रम में छात्रों के ग्रेड का विश्लेषण करके देख सकते हैं कि क्या दोनों विषयों के औसत के बीच कोई महत्वपूर्ण अंतर है। इस मामले में, प्रत्येक छात्र का गणित ग्रेड उसी छात्र के सांख्यिकी ग्रेड से जुड़ा हुआ है।

युग्मित या संबंधित नमूनों के लिए विद्यार्थी का टी-परीक्षण सूत्र है:

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

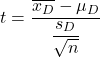
सोना:

$t$

युग्मित साधनों के लिए परिकल्पना परीक्षण आँकड़ा है, जिसे छात्र के टी वितरण द्वारा परिभाषित किया गया है।
$\overline{x_D}$

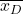
डेटा में अंतर से बने नमूने का माध्य है।
$\mu_D$

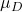
परिकल्पना परीक्षण में प्रस्तावित माध्य का मान है।
$s_D$

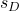
डेटा में अंतर से बने नमूने का मानक विचलन है।
$n$

नमूना आकार है.

विद्यार्थी की टी-टेस्ट धारणाएँ

विद्यार्थी का टी-टेस्ट करने के लिए, निम्नलिखित शर्तों को पूरा करना होगा:

निरंतरता – नमूना डेटा निरंतर है।
यादृच्छिकता : डेटा नमूने यादृच्छिक रूप से चुने गए थे।
समरूपता : डेटा नमूने का विचरण सजातीय है।
सामान्यता – डेटा नमूने को परिभाषित करने वाला वितरण लगभग सामान्य है।

विद्यार्थी का टी टेस्ट कैसे करें

अंत में, संक्षेप में, छात्र का परीक्षण करने के लिए अनुसरण किए जाने वाले चरण विस्तृत हैं।

परिकल्पना परीक्षण की शून्य और वैकल्पिक परिकल्पनाओं को परिभाषित करें।
परिकल्पना परीक्षण का महत्व स्तर (α) स्थापित करें।
सत्यापित करें कि छात्र के टी-टेस्ट की धारणाएँ पूरी हुई हैं।
संबंधित छात्र के टी-परीक्षण सूत्र को लागू करें और परीक्षण आंकड़ों की गणना करें।
छात्र के टी परीक्षण के परिणाम की तुलना परीक्षण के महत्वपूर्ण मूल्य से करके करें।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

विद्यार्थी का टी-टेस्ट क्या है?

विद्यार्थियों के टी-परीक्षणों के प्रकार

विद्यार्थी के टी-टेस्ट का एक नमूना

स्वतंत्र नमूनों के लिए विद्यार्थी का टी परीक्षण

अज्ञात और समान विचलन

अज्ञात और विभिन्न विविधताएँ

युग्मित या संबंधित नमूनों के लिए विद्यार्थी का टी परीक्षण

विद्यार्थी की टी-टेस्ट धारणाएँ

विद्यार्थी का टी टेस्ट कैसे करें

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने