समलैंगिकता

यह आलेख बताता है कि सांख्यिकी में समलैंगिकता क्या है। तो, आपको समरूपता की परिभाषा मिलेगी, एक प्रतिगमन मॉडल में समरूपता न होने के क्या कारण हैं और और भी बहुत कुछ, इसे कैसे ठीक किया जाए।

समलैंगिकता क्या है?

समरूपता एक प्रतिगमन मॉडल की एक विशेषता है जिसके व्याख्यात्मक चर की त्रुटियों में निरंतर भिन्नता होती है। अर्थात्, जब एक प्रतिगमन मॉडल का त्रुटि विचरण स्थिर होता है, तो उक्त मॉडल समरूपता प्रदर्शित करता है और इसलिए, यह एक समरूप मॉडल है।

याद रखें कि त्रुटि (या अवशिष्ट) को वास्तविक मूल्य और प्रतिगमन मॉडल द्वारा अनुमानित मूल्य के बीच अंतर के रूप में परिभाषित किया गया है।

प्रतिगमन मॉडल चलाते समय, हमें प्रत्येक अवलोकन के लिए पिछले अभिव्यक्ति से एक अलग मूल्य मिलेगा। इस प्रकार, एक होमोस्केडास्टिक सांख्यिकीय मॉडल वह है जिसमें गणना की गई त्रुटियों का विचरण पूरे अवलोकन में स्थिर रहता है।

यह महत्वपूर्ण है कि एक प्रतिगमन मॉडल समरूपता प्रदर्शित करता है; वास्तव में, यह प्रतिगमन मॉडल की पिछली धारणाओं में से एक है। यदि अवशेष समरूपता नहीं हैं, तो समरूपता प्राप्त करने के लिए मॉडल को दूसरे तरीके से फिर से बनाना बेहतर है। अन्यथा, प्रतिगमन गुणांक का अनुमान गलत होने की संभावना है और शून्य परिकल्पनाओं को स्वीकार करने से परिकल्पना परीक्षण में त्रुटियां भी होंगी जिन्हें वास्तव में खारिज कर दिया जाना चाहिए।

समलैंगिकता की कमी के कारण

किसी मॉडल में समरूपता न होने के सबसे सामान्य कारण ये हैं:

• जब डेटा रेंज औसत की तुलना में बहुत व्यापक हो। यदि एक ही सांख्यिकीय नमूने में बहुत बड़े मूल्य और बहुत छोटे मूल्य हैं, तो यह संभावना है कि प्राप्त प्रतिगमन मॉडल समरूप नहीं है।
• प्रतिगमन मॉडल में चर छोड़ने से भी समरूपता की कमी होती है। तार्किक रूप से, यदि एक प्रासंगिक चर को मॉडल में शामिल नहीं किया गया है, तो इसकी भिन्नता को अवशेषों में शामिल किया जाएगा और जरूरी नहीं कि तय किया जाएगा।
• संरचना में बदलाव से डेटा सेट में मॉडल का खराब फिट हो सकता है और इसलिए, अवशेषों का विचरण स्थिर नहीं है।
• जब कुछ चर में अन्य व्याख्यात्मक चर की तुलना में बहुत बड़े मूल्य होते हैं, तो मॉडल में समरूपता नहीं हो सकती है। इस मामले में, समस्या को हल करने के लिए चरों को सापेक्ष बनाया जा सकता है।

हालाँकि, कुछ ऐसे मामले हैं जिन्हें समलैंगिकता के रूप में प्रस्तुत करना स्वाभाविक रूप से कठिन है। उदाहरण के लिए, यदि हम किसी व्यक्ति की आय को उनके भोजन व्यय के आधार पर मॉडल करें, तो अमीर लोगों के भोजन व्यय में गरीब लोगों की तुलना में बहुत अधिक परिवर्तनशीलता होती है। क्योंकि एक अमीर व्यक्ति कभी-कभी महंगे रेस्तरां में और कभी-कभी सस्ते रेस्तरां में खाना खाता है, इसके विपरीत एक गरीब व्यक्ति हमेशा सस्ते रेस्तरां में खाना खाता है। इसलिए, प्रतिगमन मॉडल में समरूपता प्राप्त करना कठिन है।

समरूपता प्राप्त करने के लिए डेटा को सही करना

जब प्राप्त प्रतिगमन मॉडल होमोसेडैस्टिक नहीं है, तो होमोसेडैस्टिकिटी प्राप्त करने के लिए निम्नलिखित सुधारों का प्रयास किया जा सकता है:

• स्वतंत्र चर के प्राकृतिक लघुगणक की गणना करें, यह आम तौर पर तब उपयोगी होता है जब ग्राफ़ में अवशेषों का विचरण बढ़ता है।
• अवशिष्ट कथानक के आधार पर, स्वतंत्र चर का एक अन्य प्रकार का परिवर्तन अधिक व्यावहारिक हो सकता है। उदाहरण के लिए, यदि ग्राफ़ एक परवलय के आकार में है, तो हम स्वतंत्र चर के वर्ग की गणना कर सकते हैं और उस चर को मॉडल में जोड़ सकते हैं।
• मॉडल के लिए अन्य चर का भी उपयोग किया जा सकता है; किसी चर को हटाकर या जोड़कर, अवशेषों के विचरण को संशोधित किया जा सकता है।
• न्यूनतम वर्ग मानदंड का उपयोग करने के बजाय, भारित न्यूनतम वर्ग मानदंड का उपयोग किया जा सकता है।

समरूपता और विषमलैंगिकता

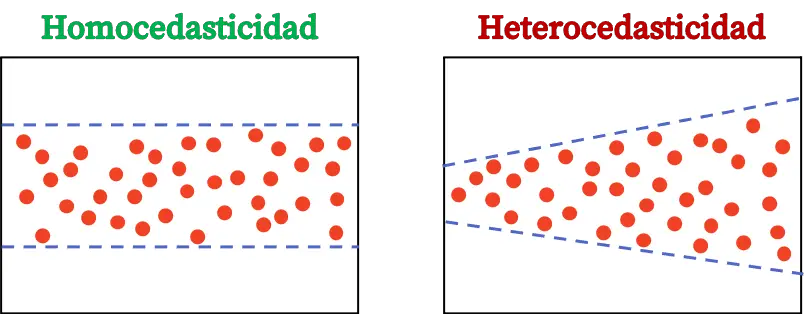
अंत में, हम देखेंगे कि समरूपता और विषमलैंगिकता के बीच क्या अंतर है, क्योंकि वे प्रतिगमन मॉडल की दो महत्वपूर्ण सांख्यिकीय अवधारणाएँ हैं।

विषमलैंगिकता एक सांख्यिकीय विशेषता है जिसका अर्थ है कि प्रतिगमन मॉडल के अवशेषों में निरंतर भिन्नता नहीं होती है, जिससे त्रुटियों की परिवर्तनशीलता पूरे कथानक में समान नहीं होती है।

समरूपता और विषमलैंगिकता के बीच का अंतर त्रुटि विचरण की स्थिरता है। समरूपता का अर्थ है कि त्रुटि विचरण स्थिर है, जबकि विषमलैंगिकता का अर्थ है कि त्रुटि विचरण स्थिर नहीं है।