R में loess प्रतिगमन कैसे करें (उदाहरण के साथ)

LOESS प्रतिगमन , जिसे कभी-कभी स्थानीय प्रतिगमन भी कहा जाता है, एक ऐसी विधि है जो डेटा के एक सेट में प्रतिगमन मॉडल को फिट करने के लिए स्थानीय समायोजन का उपयोग करती है।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि R में LOESS प्रतिगमन कैसे करें।

चरण 1: डेटा बनाएं

सबसे पहले, आइए R में निम्नलिखित डेटा फ़्रेम बनाएं:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

चरण 2: एकाधिक LOESS प्रतिगमन मॉडल फ़िट करें

हम स्पैन पैरामीटर के लिए विभिन्न मानों का उपयोग करके, इस डेटासेट में एकाधिक LOESS प्रतिगमन मॉडल को फिट करने के लिए loess() फ़ंक्शन का उपयोग कर सकते हैं:

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

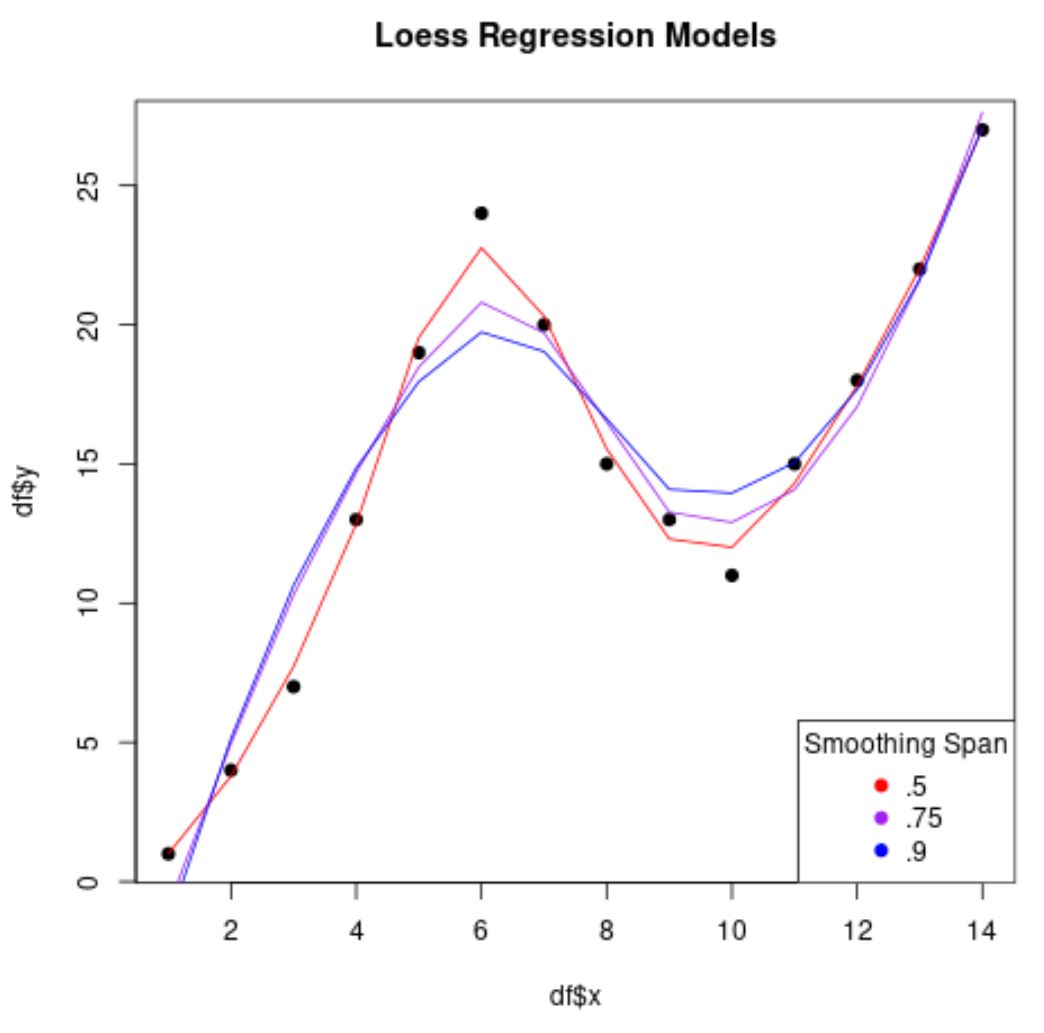
ध्यान दें कि हम स्पैन के लिए जितना कम मूल्य का उपयोग करेंगे, प्रतिगमन मॉडल उतना ही कम “सुचारू” होगा और उतना ही अधिक मॉडल डेटा बिंदुओं को फिट करने का प्रयास करेगा।

चरण 3: सर्वश्रेष्ठ मॉडल खोजने के लिए के-फोल्ड क्रॉस-वैलिडेशन का उपयोग करें

उपयोग के लिए इष्टतम सीमा मान खोजने के लिए, हम कैरेट पैकेज में फ़ंक्शन का उपयोग करके के-फ़ोल्ड क्रॉस-सत्यापन कर सकते हैं:

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

हम देख सकते हैं कि मूल माध्य वर्ग त्रुटि (आरएमएसई) के लिए न्यूनतम मान उत्पन्न करने वाला स्पैन मान 0.7 है।

इसलिए, हमारे अंतिम LOESS प्रतिगमन मॉडल के लिए, हम loess() फ़ंक्शन में स्पैन तर्क के लिए 0.7 के मान का उपयोग करना चुनेंगे।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल आर में प्रतिगमन मॉडल के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में लॉजिस्टिक रिग्रेशन कैसे करें
आर में क्वांटाइल रिग्रेशन कैसे करें
आर में भारित प्रतिगमन कैसे करें