शून्य के मानक विचलन की व्याख्या कैसे करें

आंकड़ों में, मानक विचलन का उपयोग किसी नमूने में मूल्यों के वितरण को मापने के लिए किया जाता है।

किसी दिए गए नमूने के मानक विचलन की गणना के लिए हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

√ Σ(x _i – x _bar ) ² / (n-1)

सोना:

• Σ: एक प्रतीक जिसका अर्थ है “योग”
• x _i : नमूने का ⁱ वां मान
• x _बार : नमूना का मतलब है
• n: नमूना आकार

मानक विचलन मान जितना अधिक होगा, नमूने में मान उतने ही अधिक बिखरे हुए होंगे।

मानक विचलन मान जितना कम होगा, मान उतने ही अधिक बारीकी से एक साथ समूहीकृत होंगे।

यदि किसी नमूने का मानक विचलन शून्य है, तो इसका मतलब है कि नमूने में सभी मान बिल्कुल समान हैं।

दूसरे शब्दों में, मूल्यों के बीच कोई अंतर नहीं है।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में शून्य के मानक विचलन की व्याख्या कैसे की जाए।

उदाहरण: शून्य के मानक विचलन की व्याख्या कैसे करें

मान लीजिए कि हम 10 छिपकलियों का एक सरल यादृच्छिक नमूना एकत्र करते हैं और उनकी लंबाई (इंच में) मापते हैं:

लंबाई : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7

नमूने में छिपकलियों की औसत लंबाई 7 इंच है।

यह जानकर, हम इस डेटा सेट के लिए नमूना मानक विचलन की गणना कर सकते हैं:

• s = √ Σ(x _i – x _bar ) ² / (n-1)
• s = √ ((7 – 7) ² + (7 – 7) ² + (7 – 7) ² + … + (7 – 7) ² / (10-1)
• s = √ 0 ² + 0 ² + 0 ² + … + 0 ² / 9
• एस = 0

नमूना मानक विचलन 0 निकला।

चूँकि प्रत्येक छिपकली की लंबाई बिल्कुल समान है, इसलिए डेटासेट में मानों का वितरण बिल्कुल शून्य है।

क्या वास्तविक दुनिया में मानक विचलन कभी शून्य होगा?

वास्तविक दुनिया के डेटा सेट के लिए शून्य का मानक विचलन होना पूरी तरह से संभव है, लेकिन यह दुर्लभ है।

सबसे संभावित परिदृश्य जिसमें आपको शून्य के मानक विचलन का सामना करना पड़ सकता है वह दुर्लभ घटनाओं के लिए छोटे नमूने एकत्र करते समय होगा।

उदाहरण के लिए, मान लीजिए कि आप एक निश्चित शहर में एक सप्ताह की अवधि में सड़क दुर्घटनाओं की संख्या पर डेटा एकत्र करते हैं।

यह पूरी तरह संभव है कि आप निम्नलिखित डेटा एकत्र करें:

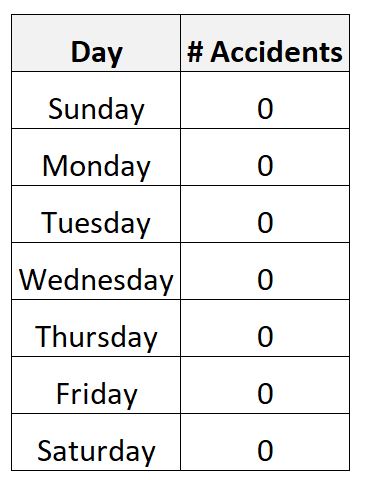
इस परिदृश्य में, दैनिक दुर्घटनाओं की औसत संख्या शून्य होगी और मानक विचलन भी शून्य होगा।

या शायद आप 6 महीने की अवधि में किसी व्यवसाय के लिए किसी महंगे उत्पाद की मासिक बिक्री की संख्या पर निम्नलिखित डेटा एकत्र करते हैं:

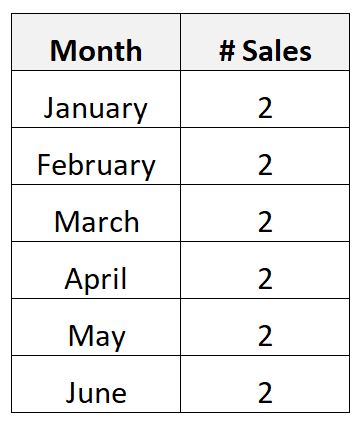
क्योंकि उत्पाद इतना महंगा है, यह पता चला है कि कंपनी प्रति माह केवल दो ही बेचती है।

इस परिदृश्य में, बेचे गए मासिक उत्पादों की औसत संख्या दो है और बेचे गए मासिक उत्पादों का मानक विचलन शून्य है।

जब भी आप वास्तविक डेटा सेट में शून्य के मानक विचलन का सामना करते हैं, तो बस यह जान लें कि इसका मतलब है कि डेटा सेट में प्रत्येक मान बिल्कुल समान है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल सांख्यिकी में मानक विचलन के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

मानक विचलन क्यों महत्वपूर्ण है?
मानक विचलन और मानक त्रुटि: क्या अंतर है?
मानक विचलन और अंतरचतुर्थक सीमा: क्या अंतर है?