नियंत्रण सीमा
यह आलेख बताता है कि नियंत्रण सीमा क्या है और नियंत्रण चार्ट की विभिन्न नियंत्रण सीमाएँ क्या हैं। आप यह भी देखेंगे कि नियंत्रण सीमाओं की गणना कैसे की जाती है और साथ ही एक उदाहरण भी देखेंगे जिसमें किसी प्रक्रिया की नियंत्रण सीमाएं निर्धारित की जाती हैं।
नियंत्रण सीमाएँ क्या हैं?
नियंत्रण सीमाएँ नियंत्रण चार्ट पर क्षैतिज रेखाएँ होती हैं जिनका उपयोग यह निर्धारित करने के लिए किया जाता है कि कोई प्रक्रिया नियंत्रित है या नहीं।
एक नियंत्रण चार्ट में दो नियंत्रण सीमाएँ होती हैं: ऊपरी और निचली नियंत्रण सीमाएँ, जो क्रमशः ऊपर और नीचे नियंत्रण क्षेत्र का सीमांकन करती हैं।
तो, नियंत्रण सीमाएँ वे मान हैं जिनका उपयोग किसी प्रक्रिया के नियंत्रण के क्षेत्र को इंगित करने के लिए किया जाता है। यदि किसी प्रक्रिया से प्राप्त माप नियंत्रण सीमा के भीतर है, तो इसका मतलब है कि प्रक्रिया नियंत्रित है। अन्यथा, मशीन या प्रक्रिया की जांच की जानी चाहिए क्योंकि संभावना है कि यह भटक गई है।
नियंत्रण सीमा के प्रकार
नियंत्रण सीमाएँ हैं:
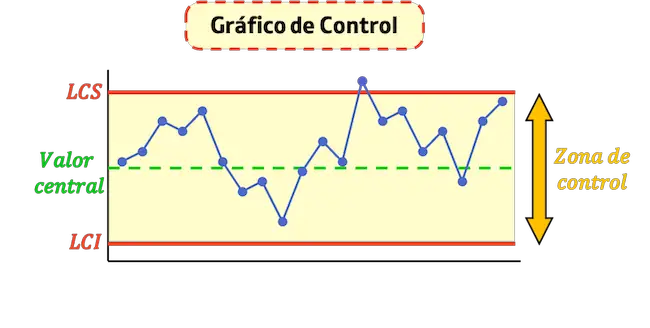
- ऊपरी नियंत्रण सीमा (LCS) : यह वह रेखा है जो प्रक्रिया में स्वीकृत अधिकतम मूल्य को इंगित करती है।
- निचली नियंत्रण सीमा (एलसीआई) : यह वह रेखा है जो प्रक्रिया में स्वीकृत न्यूनतम मूल्य को इंगित करती है।
- केंद्रीय नियंत्रण रेखा : यह वह रेखा है जो ग्राफ़ के औसत मान को दर्शाती है। बिंदु इस रेखा के जितने करीब होंगे, प्रक्रिया उतनी ही अधिक स्थिर होगी।
नियंत्रण सीमाओं की गणना कैसे करें
वर्तमान में, किसी प्रक्रिया की नियंत्रण सीमा की गणना आम तौर पर कंप्यूटर सॉफ़्टवेयर द्वारा की जाती है जो प्रक्रिया को नियंत्रित करने की अनुमति देती है। हालाँकि, यह भी महत्वपूर्ण है कि आप जानें कि उनकी गणना कैसे की जाती है, क्योंकि आपको उन्हें मैन्युअल रूप से ढूंढने की आवश्यकता हो सकती है।
नियंत्रण चार्ट की नियंत्रण सीमा की गणना उस चार्ट के प्रकार पर निर्भर करती है जिसे आप बनाना चाहते हैं, क्योंकि मान इस पर निर्भर करेगा कि यह माध्य के लिए नियंत्रण चार्ट है या सीमा के लिए।
औसत नियंत्रण चार्ट एक ग्राफ है जिसमें किसी प्रक्रिया के औसत के विकास का मूल्यांकन किया जाता है। तो, मानों के एक सेट के औसत की गणना निम्न सूत्र का उपयोग करके की जाती है:

सोना:
-

माप संख्या i है.
-

लिए गए मापों की संख्या है.
हम माध्य के लिए नियंत्रण चार्ट का केंद्रीय मान इस प्रकार निर्दिष्ट करेंगे
![]()
, जो नमूनों का औसत है और इसकी गणना निम्नलिखित अभिव्यक्ति के साथ की जाती है:

सोना:
-
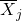
नमूना j का माध्य है.
-

लिए गए नमूनों की संख्या है.
इसके विपरीत, सीमा नियंत्रण चार्ट का केंद्रीय मूल्य लिए गए सभी नमूनों की सीमा का औसत है:

सोना:
-
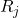
नमूना जे की सीमा है।
-

लिए गए नमूनों की संख्या है.
इस प्रकार, नियंत्रण चार्ट की नियंत्रण सीमा की गणना के सूत्र इस प्रकार हैं:
नियंत्रण कार्ड
![Rendered by QuickLaTeX.com \begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-fea27f2cb07784e5d8f7e128a010a02c_l3.png)
आर नियंत्रण कार्ड
![Rendered by QuickLaTeX.com \begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5d3cf71032f18cd8710d9a2165d8daac_l3.png)
जहां पैरामीटर ए 2 , डी 3 और डी 4 के मान निम्न तालिका में पाए जाते हैं:
| आकार (सं.) | 2 बजे | दिन 3 | जे4 |
|---|---|---|---|
| 2 | 1,880 | 0.000 | 3,267 |
| 3 | 1,023 | 0.000 | 2,575 |
| 4 | 0.729 | 0.000 | 2,282 |
| 5 | 0.577 | 0.000 | 2,115 |
| 6 | 0.483 | 0.000 | 2004 |
| 7 | 0.419 | 0.076 | 1,924 |
| 8 | 0.373 | 0.136 | 1,864 |
| 9 | 0.337 | 0.184 | 1,816 |
| दस | 0.308 | 0.223 | 1,777 |
नियंत्रण सीमा की गणना का उदाहरण
एक औद्योगिक कंपनी यह देखने के लिए सिलेंडर के व्यास के माप को नियंत्रित करना चाहती है कि उसकी उत्पादन प्रक्रिया नियंत्रण में है या नहीं। ऐसा करने के लिए, हर 15 मिनट में 5 सिलेंडरों का एक नमूना लें और उनका व्यास मापें। निम्न तालिका माप रिकॉर्डिंग दिखाती है।

नियंत्रण सीमाएँ ज्ञात करने के लिए, हमें पहले माप के प्रत्येक सेट का अंकगणितीय माध्य और सीमा लेनी होगी:

आइए अब माध्य और श्रेणियों के औसत की गणना करें, जो क्रमशः औसत और सीमा के लिए नियंत्रण चार्ट के केंद्रीय मान होंगे:


इस मामले में, प्रत्येक नमूना 5 मापों से बना है, इसलिए नियंत्रण सीमा सूत्रों के गुणांक इस प्रकार हैं:
![]()
![]()
![]()
हम औसत और विस्तारित नियंत्रण चार्ट की ऊपरी और निचली नियंत्रण सीमाओं की गणना करते हैं:
नियंत्रण चार्ट नियंत्रण सीमाएँ
![Rendered by QuickLaTeX.com \begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c36f6b368a9a737de0ad139fd3a3953c_l3.png)
की नियंत्रण सीमा आर नियंत्रण कार्ड
![Rendered by QuickLaTeX.com \begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4f60f6739025a68d8e145d789bf3edea_l3.png)
इसलिए व्यायाम नियंत्रण कार्ड इस प्रकार हैं:


पहले नियंत्रण चार्ट में हम देख सकते हैं कि दो मान निचली नियंत्रण सीमा से कम हैं। इसके अतिरिक्त, दूसरे नियंत्रण चार्ट में, ऊपरी नियंत्रण सीमा से ऊपर का मान भी है। इसलिए प्रक्रिया नियंत्रित नहीं है.