असमान नमूना आकारों के साथ टी-परीक्षण कैसे करें
जब सांख्यिकी की बात आती है तो छात्र अक्सर एक प्रश्न पूछते हैं:
जब प्रत्येक समूह का नमूना आकार समान न हो तो क्या टी-परीक्षण करना संभव है?
संक्षिप्त उत्तर:
हां, जब नमूना आकार बराबर न हो तो आप टी-परीक्षण कर सकते हैं। समान नमूना आकार टी-टेस्ट में की गई धारणाओं में से एक नहीं है।
वास्तविक समस्याएँ तब उत्पन्न होती हैं जब दो नमूनों में समान भिन्नताएँ नहीं होती हैं, जो कि टी-परीक्षण में की गई धारणाओं में से एक है ।
जब ऐसा होता है, तो इसके बजाय वेल्च के टी-टेस्ट का उपयोग करने की अनुशंसा की जाती है, जो समान भिन्नताओं को नहीं मानता है।
निम्नलिखित उदाहरण दिखाते हैं कि असमान नमूना आकारों के साथ टी परीक्षण कैसे करें जब भिन्नताएं समान हों और जब वे समान न हों।
उदाहरण 1: असमान नमूना आकार और समान भिन्नताएँ
मान लीजिए कि हम छात्रों को कुछ परीक्षाओं में बेहतर प्रदर्शन करने में मदद करने के लिए डिज़ाइन किए गए दो कार्यक्रम संचालित करते हैं।
परिणाम इस प्रकार हैं:
कार्यक्रम 1:
- n (नमूना आकार): 500
- x (नमूना औसत): 80
- s (नमूना मानक विचलन): 5
कार्यक्रम 2:
- n (नमूना आकार): 20
- x (नमूना औसत): 85
- s (नमूना मानक विचलन): 5
निम्नलिखित कोड दिखाता है कि प्रत्येक कार्यक्रम के लिए परीक्षा अंकों के वितरण की कल्पना करने के लिए आर में एक बॉक्सप्लॉट कैसे बनाया जाए:
#make this example reproducible set. seeds (1) #create vectors to hold exam scores program1 <- rnorm(500, mean=80, sd=5) program2 <- rnorm(20, mean=85, sd=5) #create boxplots to visualize distribution of exam scores boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))
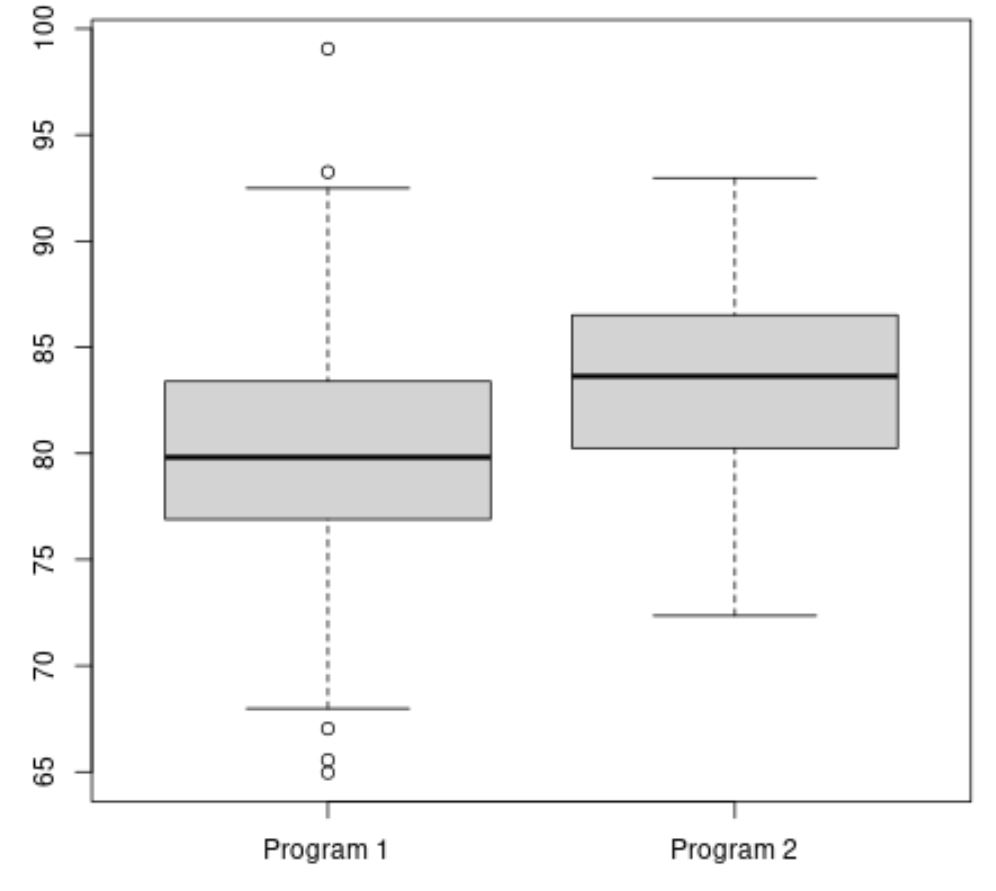
प्रोग्राम 2 के लिए औसत परीक्षा स्कोर अधिक प्रतीत होता है, लेकिन दोनों कार्यक्रमों के बीच परीक्षा स्कोर में अंतर लगभग बराबर है।
निम्नलिखित कोड दिखाता है कि वेल्च के टी-परीक्षण के साथ एक स्वतंत्र नमूना टी-परीक्षण कैसे किया जाए:
#perform independent samples t-test t. test (program1, program2, var. equal = TRUE ) Two Sample t-test data: program1 and program2 t = -3.3348, df = 518, p-value = 0.0009148 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -6.111504 -1.580245 sample estimates: mean of x mean of y 80.11322 83.95910 #perform Welch's two sample t-test t. test (program1, program2, var. equal = FALSE ) Welch Two Sample t-test data: program1 and program2 t = -3.3735, df = 20.589, p-value = 0.00293 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -6.219551 -1.472199 sample estimates: mean of x mean of y 80.11322 83.95910
स्वतंत्र नमूने का टी-परीक्षण 0.0009 का पी-मान देता है और वेल्च का टी-परीक्षण 0.0029 का पी-मान देता है।
चूँकि प्रत्येक परीक्षण का पी-मान 0.05 से कम है, हम प्रत्येक परीक्षण में शून्य परिकल्पना को अस्वीकार कर देंगे और निष्कर्ष निकालेंगे कि दोनों कार्यक्रमों के बीच औसत परीक्षा स्कोर में सांख्यिकीय रूप से महत्वपूर्ण अंतर है।
भले ही नमूना आकार असमान हैं, स्वतंत्र नमूने टी-परीक्षण और वेल्च के टी-परीक्षण दोनों समान परिणाम देते हैं क्योंकि दोनों नमूनों में समान भिन्नताएं थीं।
उदाहरण 2: असमान नमूना आकार और असमान भिन्नताएँ
मान लीजिए कि हम छात्रों को कुछ परीक्षाओं में बेहतर प्रदर्शन करने में मदद करने के लिए डिज़ाइन किए गए दो कार्यक्रम संचालित करते हैं।
परिणाम इस प्रकार हैं:
कार्यक्रम 1:
- n (नमूना आकार): 500
- x (नमूना औसत): 80
- s (नमूना मानक विचलन): 25
कार्यक्रम 2:
- n (नमूना आकार): 20
- x (नमूना औसत): 85
- s (नमूना मानक विचलन): 5
निम्नलिखित कोड दिखाता है कि प्रत्येक कार्यक्रम के लिए परीक्षा अंकों के वितरण की कल्पना करने के लिए आर में एक बॉक्सप्लॉट कैसे बनाया जाए:
#make this example reproducible set. seeds (1) #create vectors to hold exam scores program1 <- rnorm(500, mean=80, sd=25) program2 <- rnorm(20, mean=85, sd=5) #create boxplots to visualize distribution of exam scores boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))
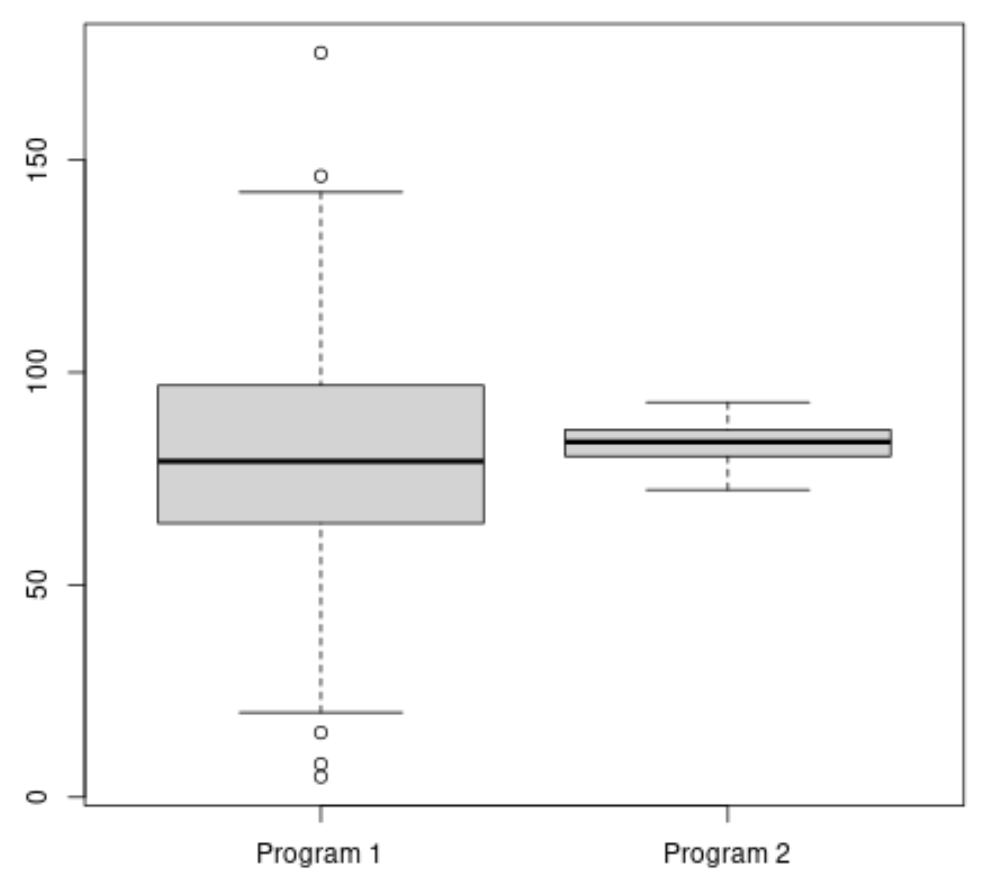
प्रोग्राम 2 के लिए औसत परीक्षा स्कोर अधिक प्रतीत होता है, लेकिन प्रोग्राम 1 के लिए परीक्षा स्कोर का अंतर प्रोग्राम 2 की तुलना में बहुत अधिक है।
निम्नलिखित कोड दिखाता है कि वेल्च के टी-परीक्षण के साथ एक स्वतंत्र नमूना टी-परीक्षण कैसे किया जाए:
#perform independent samples t-test t. test (program1, program2, var. equal = TRUE ) Two Sample t-test data: program1 and program2 t = -0.5988, df = 518, p-value = 0.5496 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -14.52474 7.73875 sample estimates: mean of x mean of y 80.5661 83.9591 #perform Welch's two sample t-test t. test (program1, program2, var. equal = FALSE ) Welch Two Sample t-test data: program1 and program2 t = -2.1338, df = 74.934, p-value = 0.03613 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -6.560690 -0.225296 sample estimates: mean of x mean of y 80.5661 83.9591
स्वतंत्र नमूने का टी-परीक्षण 0.5496 का पी-मान देता है और वेल्च का टी-परीक्षण 0.0361 का पी-मान देता है।
स्वतंत्र नमूने टी-परीक्षण औसत परीक्षा स्कोर में अंतर का पता लगाने में सक्षम नहीं है, लेकिन वेल्च का टी-परीक्षण सांख्यिकीय रूप से महत्वपूर्ण अंतर का पता लगाने में सक्षम है।
चूँकि दोनों नमूनों में असमान भिन्नताएँ थीं, केवल वेल्च का टी-परीक्षण ही औसत परीक्षा अंकों में सांख्यिकीय रूप से महत्वपूर्ण अंतर का पता लगाने में सक्षम था, क्योंकि यह परीक्षण नमूनों के बीच समान भिन्नताओं को नहीं मानता है ।
अतिरिक्त संसाधन
निम्नलिखित ट्यूटोरियल टी-परीक्षणों के बारे में अतिरिक्त जानकारी प्रदान करते हैं:
एक-नमूना टी-टेस्ट का परिचय
दो-नमूना टी परीक्षण का परिचय
युग्मित नमूने टी-परीक्षण का परिचय