आर में ओएलएस रिग्रेशन कैसे करें (उदाहरण के साथ)

साधारण न्यूनतम वर्ग (ओएलएस) प्रतिगमन एक ऐसी विधि है जो हमें एक ऐसी रेखा खोजने की अनुमति देती है जो एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध का सबसे अच्छा वर्णन करती है।

यह विधि हमें निम्नलिखित समीकरण खोजने की अनुमति देती है:

ŷ = बी ₀ + बी ₁ एक्स

सोना:

• ŷ : अनुमानित प्रतिक्रिया मूल्य
• बी ₀ : प्रतिगमन रेखा की उत्पत्ति
• बी ₁ : प्रतिगमन रेखा का ढलान

यह समीकरण हमें भविष्यवक्ता और प्रतिक्रिया चर के बीच संबंध को समझने में मदद कर सकता है, और इसका उपयोग भविष्यवक्ता चर के मूल्य को देखते हुए प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के लिए किया जा सकता है।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि आर में ओएलएस प्रतिगमन कैसे करें।

चरण 1: डेटा बनाएं

इस उदाहरण के लिए, हम 15 छात्रों के लिए निम्नलिखित दो चर वाला एक डेटासेट बनाएंगे:

• अध्ययन किए गए घंटों की कुल संख्या
• परीक्षा परीणाम

हम भविष्यवक्ता चर के रूप में घंटों और प्रतिक्रिया चर के रूप में परीक्षा स्कोर का उपयोग करके एक ओएलएस प्रतिगमन निष्पादित करेंगे।

निम्नलिखित कोड दिखाता है कि R में यह नकली डेटासेट कैसे बनाया जाए:

 #create dataset
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

चरण 2: डेटा को विज़ुअलाइज़ करें

ओएलएस रिग्रेशन करने से पहले, आइए घंटे और परीक्षा स्कोर के बीच संबंध को देखने के लिए एक स्कैटरप्लॉट बनाएं:

 library (ggplot2)

#create scatterplot
ggplot(df, aes(x=hours, y=score)) +
  geom_point(size= 2 )

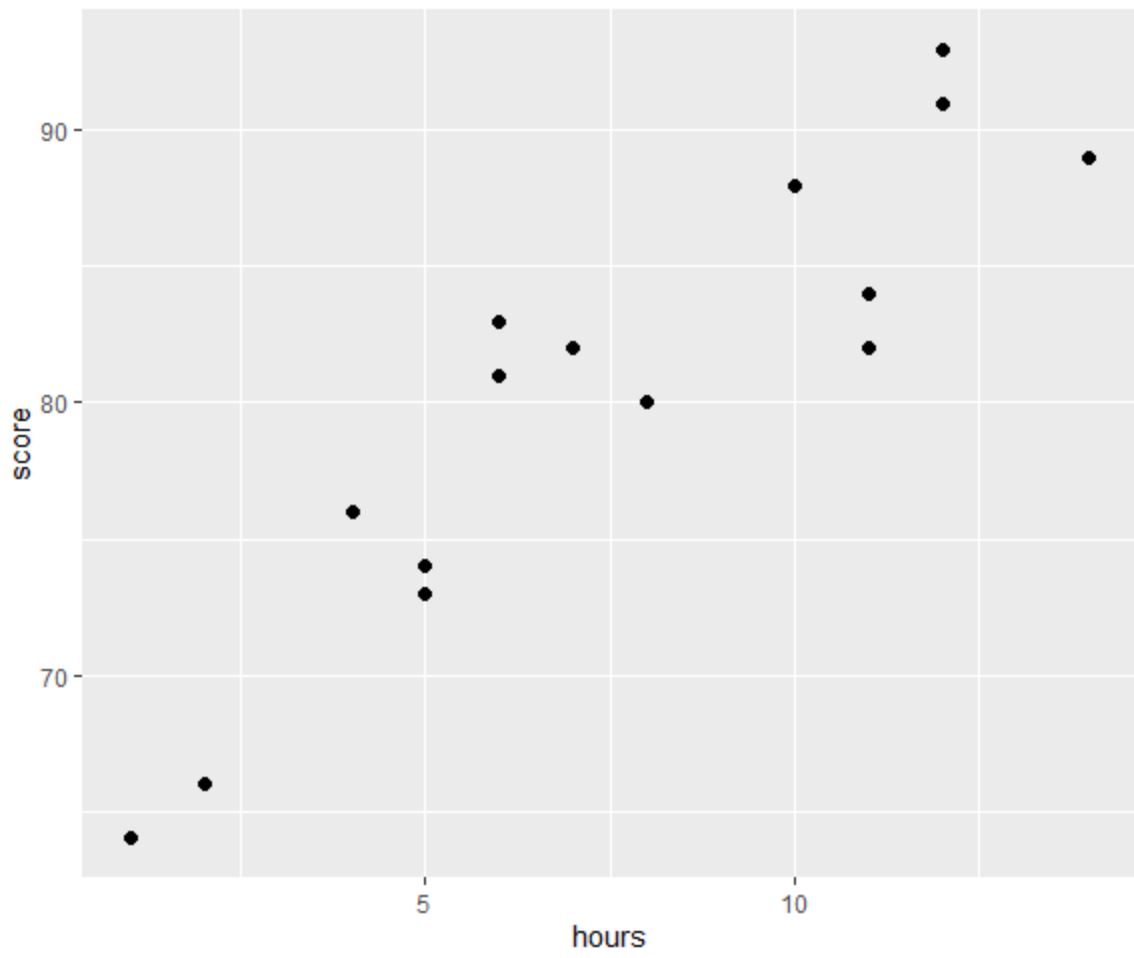
रैखिक प्रतिगमन की चार धारणाओं में से एक यह है कि भविष्यवक्ता और प्रतिक्रिया चर के बीच एक रैखिक संबंध है।

ग्राफ़ से हम देख सकते हैं कि संबंध रैखिक प्रतीत होता है। जैसे-जैसे घंटों की संख्या बढ़ती है, स्कोर भी रैखिक रूप से बढ़ने लगता है।

फिर हम परीक्षा परिणामों के वितरण की कल्पना करने और आउटलेर्स की जांच करने के लिए एक बॉक्सप्लॉट बना सकते हैं।

ध्यान दें : आर एक अवलोकन को बाह्य के रूप में परिभाषित करता है यदि यह तीसरे चतुर्थक के ऊपर अंतरचतुर्थक सीमा का 1.5 गुना है या पहले चतुर्थक के नीचे अंतरचतुर्थक सीमा का 1.5 गुना है।

यदि कोई अवलोकन बाहरी है, तो बॉक्सप्लॉट में एक छोटा वृत्त दिखाई देगा:

 library (ggplot2)

#create scatterplot
ggplot(df, aes(y=score)) +
  geom_boxplot() 

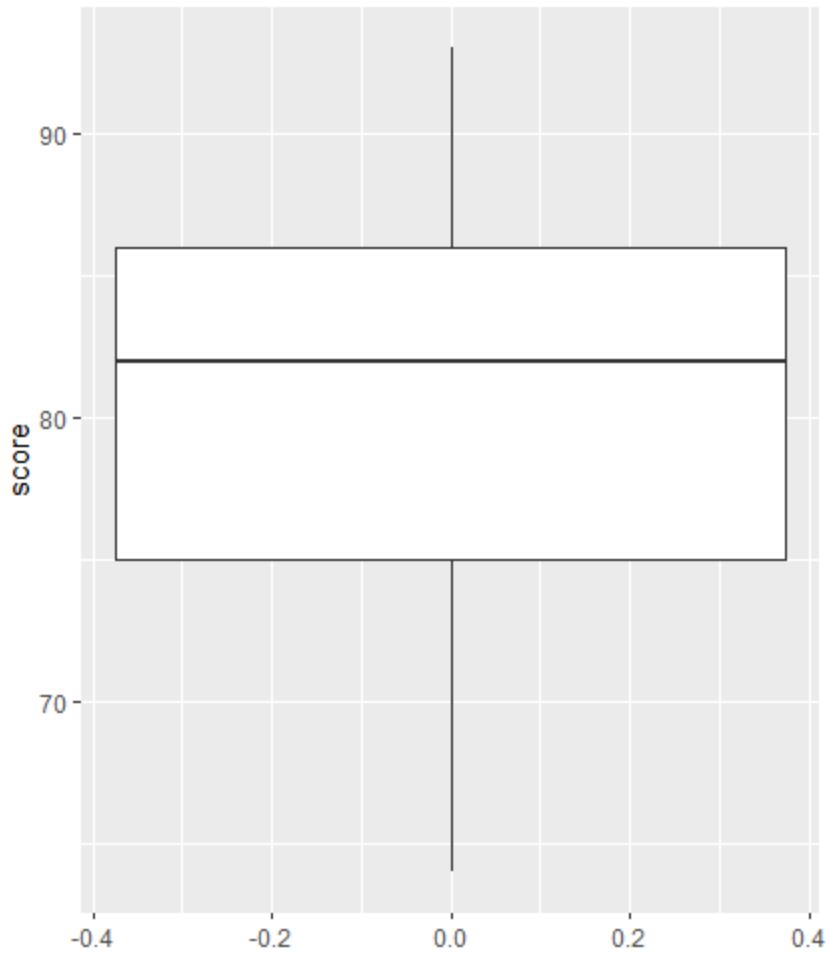
बॉक्सप्लॉट में कोई छोटे वृत्त नहीं हैं, जिसका अर्थ है कि हमारे डेटासेट में कोई आउटलेयर नहीं हैं।

चरण 3: ओएलएस रिग्रेशन करें

इसके बाद, हम ओएलएस प्रतिगमन करने के लिए आर में एलएम() फ़ंक्शन का उपयोग कर सकते हैं, घंटों को भविष्यवक्ता चर के रूप में और स्कोर को प्रतिक्रिया चर के रूप में उपयोग कर सकते हैं:

 #fit simple linear regression model
model <- lm(score~hours, data=df)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

मॉडल सारांश से, हम देख सकते हैं कि फिट किया गया प्रतिगमन समीकरण है:

स्कोर = 65.334 + 1.982*(घंटे)

इसका मतलब यह है कि अध्ययन किया गया प्रत्येक अतिरिक्त घंटा औसत परीक्षा स्कोर में 1,982 अंकों की वृद्धि से जुड़ा है।

65,334 का मूल मान हमें शून्य घंटे तक अध्ययन करने वाले छात्र के लिए औसत अपेक्षित परीक्षा स्कोर बताता है।

हम इस समीकरण का उपयोग किसी छात्र द्वारा अध्ययन किए गए घंटों की संख्या के आधार पर अपेक्षित परीक्षा स्कोर खोजने के लिए भी कर सकते हैं।

उदाहरण के लिए, एक छात्र जो 10 घंटे पढ़ाई करता है, उसे 85.15 का परीक्षा स्कोर प्राप्त करना चाहिए:

स्कोर = 65.334 + 1.982*(10) = 85.15

यहां शेष मॉडल सारांश की व्याख्या करने का तरीका बताया गया है:

• Pr(>|t|): यह मॉडल गुणांक से जुड़ा पी-मान है। चूँकि घंटों के लिए पी-वैल्यू (2.25e-06) 0.05 से काफी कम है, हम कह सकते हैं कि घंटों और स्कोर के बीच सांख्यिकीय रूप से महत्वपूर्ण संबंध है।
• एकाधिक आर-वर्ग: यह संख्या हमें बताती है कि परीक्षा के अंकों में भिन्नता का प्रतिशत अध्ययन किए गए घंटों की संख्या से समझाया जा सकता है। सामान्य तौर पर, प्रतिगमन मॉडल का आर-वर्ग मान जितना बड़ा होगा, प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने में भविष्यवक्ता चर उतना ही बेहतर होगा। इस मामले में, स्कोर में 83.1% भिन्नता को अध्ययन किए गए घंटों द्वारा समझाया जा सकता है।
• अवशिष्ट मानक त्रुटि: यह प्रेक्षित मानों और प्रतिगमन रेखा के बीच की औसत दूरी है। यह मान जितना कम होगा, प्रतिगमन रेखा प्रेक्षित डेटा के अनुरूप उतनी ही अधिक सक्षम होगी। इस मामले में, परीक्षा में देखा गया औसत स्कोर प्रतिगमन रेखा द्वारा अनुमानित स्कोर से 3,641 अंक कम हो जाता है।
• एफ-सांख्यिकी और पी-मूल्य: एफ-सांख्यिकी ( 63.91 ) और संबंधित पी-मूल्य ( 2.253ई-06 ) हमें प्रतिगमन मॉडल का समग्र महत्व बताते हैं, यानी कि मॉडल में भविष्यवक्ता चर भिन्नता को समझाने के लिए उपयोगी हैं या नहीं . प्रतिक्रिया चर में. चूँकि इस उदाहरण में पी-वैल्यू 0.05 से कम है, हमारा मॉडल सांख्यिकीय रूप से महत्वपूर्ण है और स्कोर भिन्नता को समझाने में घंटों को उपयोगी माना जाता है।

चरण 4: अवशिष्ट प्लॉट बनाएं

अंत में, हमें समरूपता और सामान्यता की धारणाओं की जांच करने के लिए अवशिष्ट प्लॉट बनाने की आवश्यकता है।

समरूपता की धारणा यह है कि प्रतिगमन मॉडल के अवशेषों में भविष्यवक्ता चर के प्रत्येक स्तर पर लगभग समान भिन्नता होती है।

यह सत्यापित करने के लिए कि यह धारणा पूरी हो गई है, हम अवशेषों बनाम फिट का एक प्लॉट बना सकते हैं।

x-अक्ष फिट किए गए मान प्रदर्शित करता है और y-अक्ष अवशिष्ट प्रदर्शित करता है। जब तक अवशेष पूरे ग्राफ़ में शून्य मान के आसपास बेतरतीब ढंग से और समान रूप से वितरित दिखाई देते हैं, तब तक हम मान सकते हैं कि समरूपता का उल्लंघन नहीं हुआ है:

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

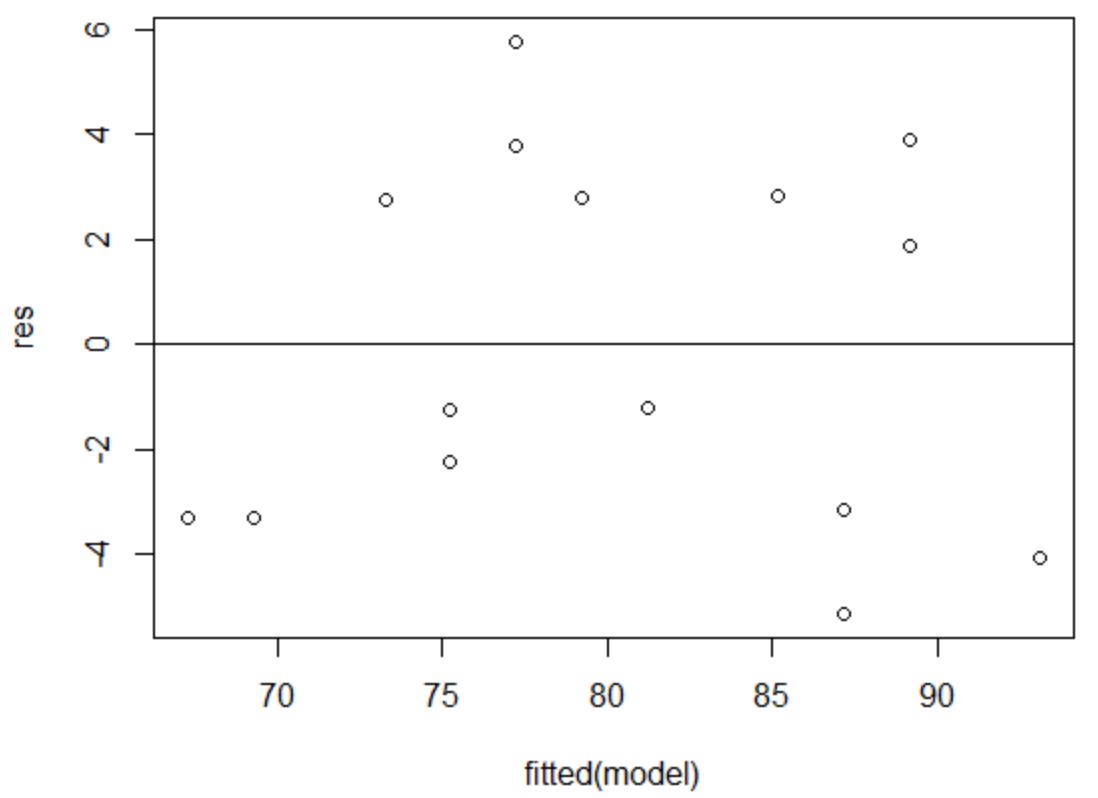
अवशेष शून्य के आसपास बेतरतीब ढंग से बिखरे हुए प्रतीत होते हैं और कोई ध्यान देने योग्य पैटर्न नहीं दिखाते हैं, इसलिए यह धारणा पूरी होती है।

सामान्यता धारणा बताती है कि एक प्रतिगमन मॉडल के अवशेष लगभग सामान्य रूप से वितरित होते हैं।

यह जांचने के लिए कि क्या यह धारणा पूरी होती है, हम एक QQ प्लॉट बना सकते हैं। यदि प्लॉट बिंदु 45 डिग्री का कोण बनाते हुए लगभग सीधी रेखा पर स्थित हैं, तो डेटा सामान्य रूप से वितरित किया जाता है:

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

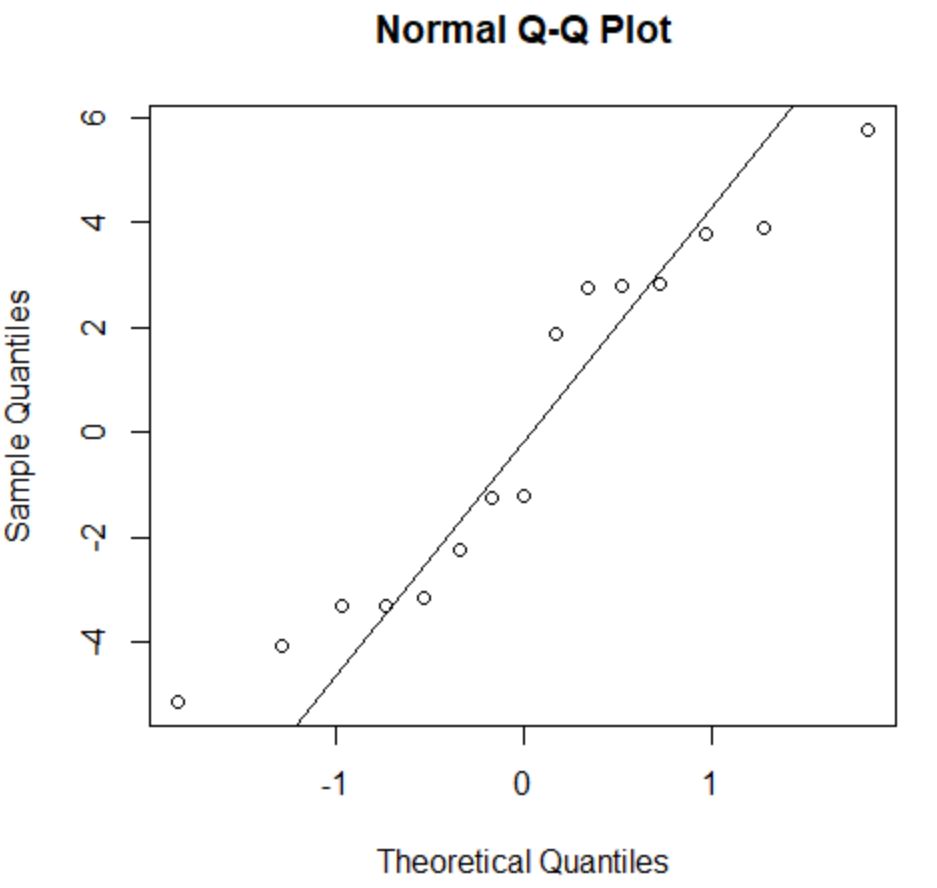
अवशेष 45 डिग्री रेखा से थोड़ा विचलित होते हैं, लेकिन गंभीर चिंता पैदा करने के लिए पर्याप्त नहीं हैं। हम मान सकते हैं कि सामान्यता की धारणा पूरी हो गई है।

चूंकि अवशेष सामान्य रूप से वितरित और होमोस्केडास्टिक होते हैं, इसलिए हमने सत्यापित किया कि ओएलएस प्रतिगमन मॉडल की धारणाएं पूरी हुई हैं।

इस प्रकार, हमारे मॉडल का आउटपुट विश्वसनीय है।

नोट : यदि एक या अधिक धारणाएँ पूरी नहीं होतीं, तो हम अपने डेटा को बदलने का प्रयास कर सकते हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर में अन्य सामान्य कार्य कैसे करें:

आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में घातीय प्रतिगमन कैसे करें
आर में भारित न्यूनतम वर्ग प्रतिगमन कैसे करें