सशर्त संभाव्यता (या सशर्त संभाव्यता)

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 6, 2023 संभावना शून्य टिप्पणियां

यहां आप जानेंगे कि सशर्त संभाव्यता (या सशर्त संभाव्यता) क्या है। हम एक उदाहरण और इस प्रकार की संभाव्यता के गुणों के साथ सशर्त संभाव्यता की गणना कैसे की जाती है, इसकी व्याख्या करते हैं। इसके अलावा, आप चरण-दर-चरण हल किए गए सशर्त संभाव्यता अभ्यासों का अभ्यास करने में सक्षम होंगे।

सशर्त संभाव्यता क्या है?

सशर्त संभाव्यता , जिसे सशर्त संभाव्यता भी कहा जाता है, एक सांख्यिकीय माप है जो इस संभावना को इंगित करता है कि यदि कोई अन्य घटना बी घटित होती है तो घटना ए घटित होगी। अर्थात्, सशर्त संभाव्यता P(A|B) घटना B के पहले ही घटित होने के बाद घटना A के घटित होने की संभावना को संदर्भित करता है।

सशर्त संभाव्यता को दो घटनाओं के बीच एक ऊर्ध्वाधर पट्टी के साथ लिखा जाता है: पी (ए | बी), और पढ़ता है: “घटना ए की सशर्त संभावना दी गई घटना बी”।

ध्यान दें कि सशर्त संभाव्यता मान 0 और 1 के बीच की एक संख्या है। सशर्त संभाव्यता जितनी अधिक होगी, घटना बी होने पर घटना ए होने की संभावना उतनी ही अधिक होगी, लेकिन सशर्त संभावना जितनी कम होगी, घटना ए होने की संभावना उतनी ही कम होगी। तब घटित होगा जब घटना बी घटित होगी।

सशर्त संभाव्यता सूत्र

घटना ए की दी गई घटना बी की सशर्त संभावना घटना ए और घटना बी के बीच प्रतिच्छेदन की संभावना को घटना बी की संभावना से विभाजित करने के बराबर है।

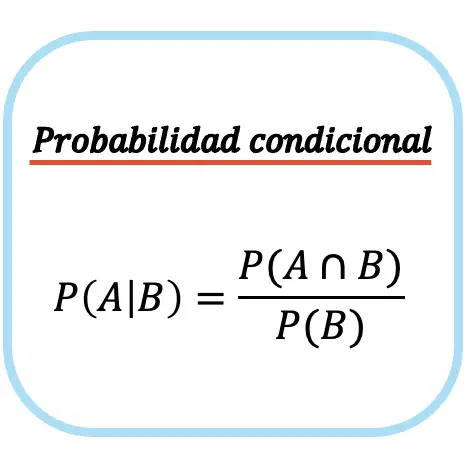
ध्यान दें कि सशर्त संभाव्यता (या सशर्त संभाव्यता) सूत्र का उपयोग केवल तभी किया जा सकता है जब बिना शर्त घटना के घटित होने की संभावना गैर-शून्य है, अर्थात P(B)≠0। या दूसरे शब्दों में, यदि घटना बी का घटित होना संभव है।

सशर्त संभाव्यता की गणना इसके व्युत्क्रम से भी की जा सकती है, अर्थात यदि P(B|A) ज्ञात है, तो P(A|B) निर्धारित किया जा सकता है। लेकिन ऐसा करने के लिए आपको बेयस प्रमेय लागू करना होगा, आप यहां देख सकते हैं कि इस प्रमेय में क्या शामिल है:

➤ देखें: बेयस प्रमेय क्या है?

सशर्त संभाव्यता का उदाहरण

एक बार जब हमने देख लिया कि सशर्त संभाव्यता की परिभाषा और सूत्र क्या है, तो हम इसके अर्थ को पूरी तरह से समझने के लिए चरण दर चरण इस प्रकार की संभाव्यता का एक उदाहरण हल करेंगे।

30 छात्रों की एक कक्षा में परीक्षा देने के बाद, यह पता लगाने के लिए डेटा एकत्र किया गया कि कितने छात्रों ने अध्ययन किया और कितने उत्तीर्ण हुए। परिणाम निम्नलिखित आकस्मिकता तालिका में प्रस्तुत किए गए हैं। एकत्रित आंकड़ों से, यदि आपने पहले ही अध्ययन कर लिया है तो परीक्षा उत्तीर्ण करने की सशर्त संभावना की गणना करें।

सशर्त संभाव्यता प्राप्त करने के लिए, हमें वह सूत्र लागू करना होगा जो हमने पहले देखा था:

$P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}$

इसलिए, हमें सबसे पहले इस संभावना को खोजना होगा कि एक छात्र ने पढ़ाई की और पढ़ाई की और उत्तीर्ण हो गया। किसी छात्र द्वारा अध्ययन किए जाने की संभावना ज्ञात करने के लिए, हमें बस लाप्लास के नियम का उपयोग करने की आवश्यकता है, अर्थात, हम अध्ययन करने वाले छात्रों की संख्या को अवलोकनों की कुल संख्या से विभाजित करते हैं:

$P(\text{estudiado})=\cfrac{23}{30}=0,77$

और हम आकस्मिकता तालिका से एक ही समय में पढ़ने वाले और उत्तीर्ण होने वाले छात्रों की संख्या को कुल से विभाजित करके इस संभावना का पता लगा सकते हैं कि एक छात्र ने एक ही समय में अध्ययन किया और उत्तीर्ण हुआ:

$P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63$

इस प्रकार, यदि किसी छात्र ने पढ़ाई की है तो परीक्षा उत्तीर्ण करने की प्रायिकता है:

$\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}$

आश्रित और स्वतंत्र घटनाओं की सशर्त संभावना

इस अनुभाग में हम देखेंगे कि सशर्त संभाव्यता और आश्रित और स्वतंत्र घटनाओं (या आश्रित और स्वतंत्र घटनाओं) के बीच क्या संबंध है। क्योंकि, यद्यपि वे अलग-अलग अवधारणाएँ हैं, ये दो प्रकार की घटनाएँ एक सशर्त संभाव्यता से जुड़ी हुई हैं।

दो घटनाएँ (या घटनाएँ) स्वतंत्र होती हैं जब उनके घटित होने की संभावना एक दूसरे पर निर्भर नहीं होती है। ऐसे मामले में, दो घटनाओं के बीच का प्रतिच्छेदन प्रत्येक घटना की अलग-अलग संभावना के उत्पाद के बराबर होता है। और, इसलिए, सशर्त संभाव्यता सूत्र सरल है:

$P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)$

संक्षेप में, यदि घटनाएँ A और B स्वतंत्र हैं, तो घटना A की दी गई घटना B की सशर्त संभावना, घटना A के घटित होने की संभावना के बिल्कुल बराबर है।

दूसरी ओर, जब दो घटनाएँ निर्भर होती हैं, तो इसका मतलब है कि एक घटना की संभावना दूसरी घटना की संभावना पर निर्भर करती है। इसलिए, जब दो घटनाएं ए और बी निर्भर होती हैं, तो घटना ए की दी गई घटना बी की सशर्त संभावना घटना ए की घटना की संभावना से भिन्न होती है।

$P(A|B)\neq P(A)$

सशर्त संभाव्यता अभ्यासों को हल किया गया

अभ्यास 1

हम जानते हैं कि गेंदों से भरे बैग में आधा नारंगी और दूसरा हरा है। इसके अलावा, सभी गेंदों में से एक तिहाई नारंगी हैं और साथ ही एक चिन्ह से चिह्नित हैं। इसकी क्या प्रायिकता है कि जब आप एक नारंगी गेंद निकालेंगे तो उसे संकेत प्राप्त होगा?

समाधान देखें

अभ्यास को हल करने के लिए, हमें सशर्त सूत्र संभाव्यता को लागू करना होगा, जो है:

$P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}$

समस्या कथन हमें बताता है कि आधा बैग संतरे का है। इसलिए, नारंगी गेंद को उठाने की सैद्धांतिक संभावना 50% है।

$P(\text{naranja})=\cfrac{1}{2}=0,5$

दूसरी ओर, हम जानते हैं कि कुल में से एक तिहाई नारंगी गेंदें हैं और उनमें एक सिग्नल है, इसलिए सिग्नल के साथ एक नारंगी गेंद प्राप्त करने की संभावना है:

$P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33$

अंत में, हम इसका मान ज्ञात करने के लिए परिकलित संभावनाओं को सशर्त संभाव्यता सूत्र में प्रतिस्थापित करते हैं:

$\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}$

संक्षेप में, यदि गेंद नारंगी है तो सिग्नल के साथ गेंद निकालने की संभावना 66% है।

व्यायाम 2

यदि हमारे पास एक बॉक्स में छह नीले पेन और तीन काले पेन हैं, तो एक नीले पेन को निकालने की प्रायिकता और लगातार दो नीले पेन निकालने की प्रायिकता की गणना करें।

समाधान देखें

एक बार नीला पेन उठाने की संभावना निर्धारित करने के लिए, बस लाप्लास के नियम का उपयोग करें:

$P(\text{azul})=\cfrac{6}{6+3}=0,67$

समस्या हमें लगातार दो नीले पेन उठाने की संभावना जानने के लिए भी कहती है, यानी, अगर हम पहले ही नीला पेन उठा चुके हैं तो नीला पेन उठाने की सशर्त संभावना।

यदि हम एक नीला पेन निकालते हैं, तो हमारे पास कम अनुकूल मामला होता है, लेकिन कुल में एक पेन कम भी होता है। सशर्त संभाव्यता इसलिए है:

$P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63$

व्यायाम 3

यह देखते हुए कि एक सिक्के को उछालने पर चित आता है, पासे को संख्या 4 पर लुढ़काने की सशर्त संभावना क्या है?

समाधान देखें

इस अभ्यास को हल करने के लिए, आपको सशर्त संभाव्यता के सिद्धांत को ध्यान में रखना होगा, क्योंकि घटनाएँ “पासा फेंककर संख्या 4 प्राप्त करना” और “सिक्का उछालकर चित प्राप्त करना” स्वतंत्र हैं। इसलिए सशर्त संभाव्यता सूत्र का उपयोग करना आवश्यक नहीं है, लेकिन निम्नलिखित समानता संतुष्ट है:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})$

तो, सशर्त संभाव्यता खोजने के लिए, बस लाप्लास के नियम का उपयोग करें:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167$

व्यायाम 4

एक देश में 25 कंपनियों के वित्तीय वर्ष का अध्ययन किया गया और वर्ष के आर्थिक परिणाम के आधार पर उनके स्टॉक की कीमतें कैसे बदलती हैं। आप एकत्रित डेटा को निम्नलिखित आकस्मिकता तालिका में देख सकते हैं:

यदि किसी कंपनी ने पिछले वर्ष लाभ कमाया हो तो उसके शेयर की कीमत बढ़ने की कितनी संभावना है?

समाधान देखें

अभ्यास हमसे सशर्त संभावना के बारे में पूछता है कि कंपनी ने सकारात्मक आर्थिक परिणाम हासिल किया है, तो स्टॉक में वृद्धि होगी। इसलिए, इस संभाव्यता की गणना करने के लिए, हमें सशर्त संभाव्यता सूत्र का उपयोग करना चाहिए:

$P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}$

इसलिए हम सबसे पहले इस संभावना की गणना करते हैं कि एक कंपनी लाभ कमाती है और दूसरी, इस संभावना की गणना करते हैं कि एक कंपनी प्रति शेयर कीमत बढ़ाते हुए आर्थिक लाभ कमाती है:

$P(\text{beneficio})=\cfrac{14}{25}=0,56$

$P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4$

और फिर हम पाए गए मानों को सूत्र में प्रतिस्थापित करते हैं और सशर्त संभाव्यता की गणना करते हैं:

$\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}$

सशर्त संभाव्यता के गुण

सशर्त संभाव्यता या सशर्त संभाव्यता के गुण इस प्रकार हैं:

घटना A की सशर्त संभाव्यता और दी गई घटना B की पूरक घटना A की सशर्त संभाव्यता का योग एक के बराबर है।

$P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1$

यदि घटना A, घटना B का एक उपसमुच्चय है, तो A हमेशा तब घटित होगा जब B सत्य है। इस प्रकार, इन मामलों में घटना बी दी गई घटना ए की सशर्त संभावना 1 है।

$B\subseteq A \ \longrightarrow \ P(A|B)=1$

दो अलग-अलग घटनाओं को देखते हुए, सशर्त संभाव्यता के संबंध में निम्नलिखित समानता हमेशा बनी रहती है:

$P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

सशर्त संभाव्यता क्या है?

सशर्त संभाव्यता सूत्र

सशर्त संभाव्यता का उदाहरण

आश्रित और स्वतंत्र घटनाओं की सशर्त संभावना

सशर्त संभाव्यता अभ्यासों को हल किया गया

अभ्यास 1

व्यायाम 2

व्यायाम 3

व्यायाम 4

सशर्त संभाव्यता के गुण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने