केंद्रीय सीमा प्रमेय

यह आलेख बताता है कि केंद्रीय सीमा प्रमेय (सीएलटी) क्या है और आंकड़ों में इसका उपयोग किस लिए किया जाता है। आपको यह भी मिलेगा कि केंद्रीय सीमा प्रमेय का सूत्र क्या है और इसके अनुप्रयोग का एक उदाहरण चरण दर चरण हल किया गया है।

केंद्रीय सीमा प्रमेय क्या है?

आंकड़ों में, केंद्रीय सीमा प्रमेय , जिसे केंद्रीय सीमा प्रमेय भी कहा जाता है, बताता है कि जनसंख्या के संभाव्यता वितरण की परवाह किए बिना, नमूना का वितरण सामान्य वितरण के करीब पहुंचता है क्योंकि नमूना आकार बढ़ता है।

अर्थात्, केंद्रीय सीमा प्रमेय कहता है कि यदि हम पर्याप्त संख्या में नमूने लेते हैं, तो उन नमूनों का माध्य एक सामान्य वितरण के बराबर अनुमानित किया जा सकता है।

इसके अतिरिक्त, केंद्रीय सीमा प्रमेय में कहा गया है कि नमूना आकार बढ़ने पर नमूना माध्य जनसंख्या माध्य के मूल्य के करीब पहुंच जाएगा। यह हमें सांख्यिकीय जनसंख्या के मापदंडों का अनुमान लगाने की अनुमति देता है। नीचे हम देखेंगे कि यह कैसे किया जाता है।

सामान्य तौर पर, यह माना जाता है कि केंद्रीय सीमा प्रमेय को लागू करने के लिए, नमूना आकार कम से कम 30 अवलोकन होना चाहिए, हालांकि यह अध्ययन किए गए चर की विशेषताओं पर निर्भर करता है।

केंद्रीय सीमा प्रमेय के कई अनुप्रयोग हैं, क्योंकि सामान्य वितरण अनुमानित सांख्यिकीय गणनाओं की अनुमति देता है, जैसे परिकल्पना परीक्षण या आत्मविश्वास अंतराल। उदाहरण के लिए, वित्त में, केंद्रीय सीमा प्रमेय का उपयोग किसी निवेश के रिटर्न और जोखिम का विश्लेषण करने के लिए किया जाता है।

केंद्रीय सीमा प्रमेय का उदाहरण

एक बार जब हमने केंद्रीय सीमा प्रमेय की परिभाषा देख ली, तो आइए इसके अर्थ को पूरी तरह से समझने के लिए एक उदाहरण देखें।

केंद्रीय सीमा प्रमेय का एक उदाहरण पासे को लुढ़काना है। डाई रोल एक अलग समान वितरण का अनुसरण करता है, क्योंकि सभी परिणाम समसंभाव्य हैं। लेकिन कई परिणामों के योग का वितरण सामान्य वितरण के करीब पहुंचता है।

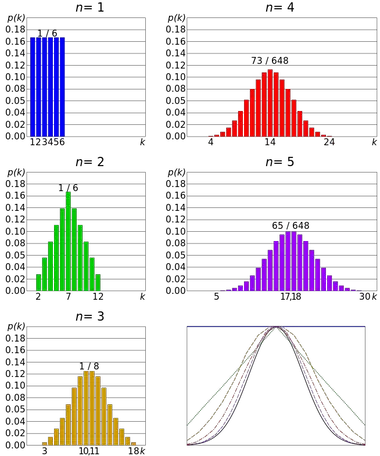
इस प्रकार, जितने अधिक थ्रो होंगे, उतनी ही अधिक संभावना होगी कि साधनों के वितरण का आकार सामान्य वितरण के ग्राफ जैसा होगा।

केंद्रीय सीमा प्रमेय सूत्र

केंद्रीय सीमा प्रमेय में कहा गया है कि यदि किसी जनसंख्या का माध्य μ और मानक विचलन σ है और हम पर्याप्त संख्या में नमूने (n≥30) लेते हैं, तो नमूना साधनों के सेट को माध्य μ और मानक विचलन σ के साथ एक सामान्य वितरण के लिए अनुमानित किया जा सकता है। /√एन.

इसके अलावा , _यदि एक्स _{1 ,} निम्नलिखित सूत्र द्वारा परिभाषित सामान्य वितरण के लिए:

केंद्रीय सीमा प्रमेय का हल किया गया अभ्यास

ताकि आप अवधारणा को पूरी तरह से आत्मसात कर सकें, यहां केंद्रीय सीमा प्रमेय का एक हल किया गया अभ्यास दिया गया है।

• एक कंपनी ऐसे पुर्जे बेचती है जिनका उपयोग खिलौनों के कुछ घटकों को बदलने के लिए किया जाता है। एक सिक्के का औसत वजन 300 ग्राम और मानक विचलन 50 ग्राम है। यदि किसी ग्राहक ने 100 टुकड़ों का एक बैच ऑर्डर किया है, तो क्या संभावना है कि बैच में टुकड़ों का औसत वजन 305 ग्राम से अधिक होगा? और क्या संभावना है कि 100 टुकड़ों के एक बैच का वजन 31 किलोग्राम से अधिक हो?

चूँकि बैच का आकार बड़ा है (n=100), हम समस्या को हल करने के लिए केंद्रीय सीमा प्रमेय लागू कर सकते हैं।

इस प्रकार, केंद्रीय सीमा प्रमेय सूत्र का उपयोग करके, नमूना साधनों के वितरण को निम्नलिखित मापदंडों के साथ सामान्य वितरण के लिए अनुमानित किया जा सकता है:

अब हम टाइपिंग प्रक्रिया को अंजाम देते हैं ताकि हम उस संभावना का पता लगा सकें जो अभ्यास हमसे मांगता है। ऐसा करने के लिए, हमें वितरण से माध्य घटाना होगा और फिर मानक विचलन से विभाजित करना होगा:

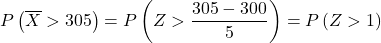सामान्य वितरण तालिका में Z>1 किस मान से मेल खाता है:

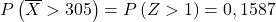
इसलिए हम टाइपिंग प्रक्रिया को दोबारा करते हैं, फिर दूसरी संभावना ढूंढते हैं कि समस्या हमसे पूछती है:

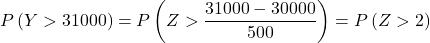
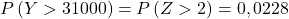➤ देखें: बड़ी संख्या का नियम