R में न्यूनतम वर्ग विधि का उपयोग कैसे करें?
न्यूनतम वर्ग विधि एक ऐसी विधि है जिसका उपयोग हम प्रतिगमन रेखा को खोजने के लिए कर सकते हैं जो डेटा के दिए गए सेट के लिए सबसे उपयुक्त है।
R में एक प्रतिगमन रेखा को फ़िट करने के लिए न्यूनतम वर्ग विधि का उपयोग करने के लिए, हम lm() फ़ंक्शन का उपयोग कर सकते हैं।
यह फ़ंक्शन निम्नलिखित मूल सिंटैक्स का उपयोग करता है:
model <- lm(response ~ predictor, data=df)
निम्नलिखित उदाहरण दिखाता है कि आर में इस फ़ंक्शन का उपयोग कैसे करें।
उदाहरण: R में न्यूनतम वर्ग विधि
मान लीजिए कि हमारे पास आर में निम्नलिखित डेटा फ्रेम है जो एक कक्षा में 15 छात्रों के लिए अध्ययन किए गए घंटों की संख्या और संबंधित परीक्षा स्कोर दिखाता है:
#create data frame df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14), score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89)) #view first six rows of data frame head(df) hours score 1 1 64 2 2 66 3 4 76 4 5 73 5 5 74 6 6 81
हम इस डेटा में एक प्रतिगमन रेखा को फिट करने के लिए कम से कम वर्ग विधि का उपयोग करने के लिए lm() फ़ंक्शन का उपयोग कर सकते हैं:
#use method of least squares to fit regression line model <- lm(score ~ hours, data=df) #view regression model summary summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -5,140 -3,219 -1,193 2,816 5,772 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 65,334 2,106 31,023 1.41e-13 *** hours 1.982 0.248 7.995 2.25e-06 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.641 on 13 degrees of freedom Multiple R-squared: 0.831, Adjusted R-squared: 0.818 F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
अनुमानित परिणाम कॉलम में मानों से, हम निम्नलिखित फिटेड रिग्रेशन लाइन लिख सकते हैं:
परीक्षा स्कोर = 65.334 + 1.982 (घंटे)
यहां मॉडल में प्रत्येक गुणांक की व्याख्या करने का तरीका बताया गया है:
- अवरोधन : 0 घंटे पढ़ाई करने वाले छात्र के लिए अपेक्षित परीक्षा स्कोर 65.334 है।
- घंटे : अध्ययन किए गए प्रत्येक अतिरिक्त घंटे के लिए, अपेक्षित परीक्षा स्कोर 1,982 बढ़ जाता है।
हम इस समीकरण का उपयोग यह अनुमान लगाने के लिए कर सकते हैं कि किसी छात्र को उसके अध्ययन के घंटों के आधार पर परीक्षा ग्रेड प्राप्त होगा।
उदाहरण के लिए, यदि कोई छात्र 5 घंटे पढ़ाई करता है, तो हमारा अनुमान है कि उसका परीक्षा स्कोर 75.244 होगा:
परीक्षा स्कोर = 65.334 + 1.982(5) = 75.244
अंत में, हम प्लॉट पर आरोपित प्रतिगमन रेखा के साथ मूल डेटा का एक स्कैटरप्लॉट बना सकते हैं:
#create scatter plot of data plot(df$hours, df$score, pch=16, col=' steelblue ') #add fitted regression line to scatter plot abline(model)
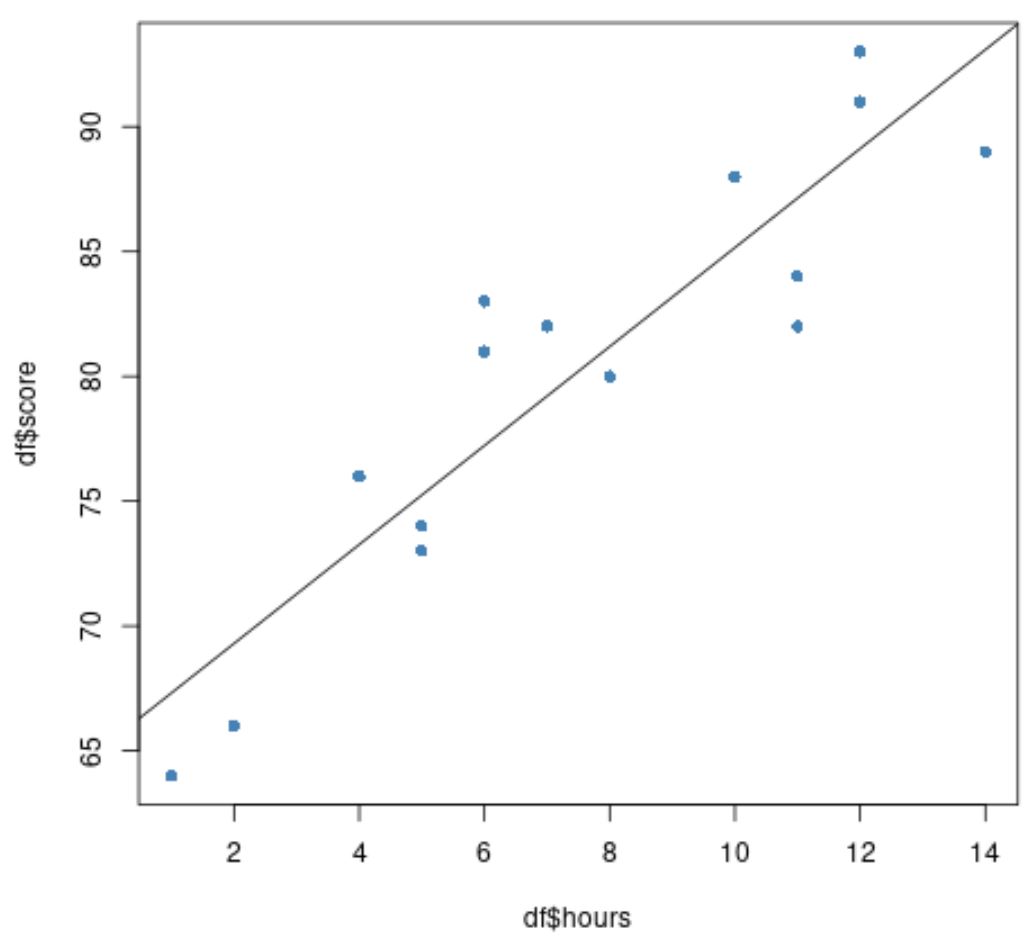
नीले वृत्त डेटा का प्रतिनिधित्व करते हैं और काली रेखा फिट प्रतिगमन रेखा का प्रतिनिधित्व करती है।
अतिरिक्त संसाधन
निम्नलिखित ट्यूटोरियल बताते हैं कि आर में अन्य सामान्य कार्य कैसे करें:
आर में अवशिष्ट प्लॉट कैसे बनाएं
आर में बहुसंरेखता का परीक्षण कैसे करें
आर में कर्व फिटिंग कैसे करें