स्किकिट-लर्न का उपयोग करके बहुपद प्रतिगमन कैसे करें

बहुपद प्रतिगमन एक ऐसी तकनीक है जिसका उपयोग हम तब कर सकते हैं जब एक पूर्वसूचक चर और एक प्रतिक्रिया चर के बीच संबंध अरेखीय होता है।

इस प्रकार का प्रतिगमन निम्न रूप लेता है:

वाई = β ₀ ⁺ β ₁ एक्स + β ₂ एक्स ² + … + β _एच

जहाँ h बहुपद की “डिग्री” है।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि स्केलेरन का उपयोग करके पायथन में बहुपद प्रतिगमन कैसे करें।

चरण 1: डेटा बनाएं

सबसे पहले, आइए एक भविष्यवक्ता और एक प्रतिक्रिया चर के मानों को रखने के लिए दो NumPy सरणियाँ बनाएँ:

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

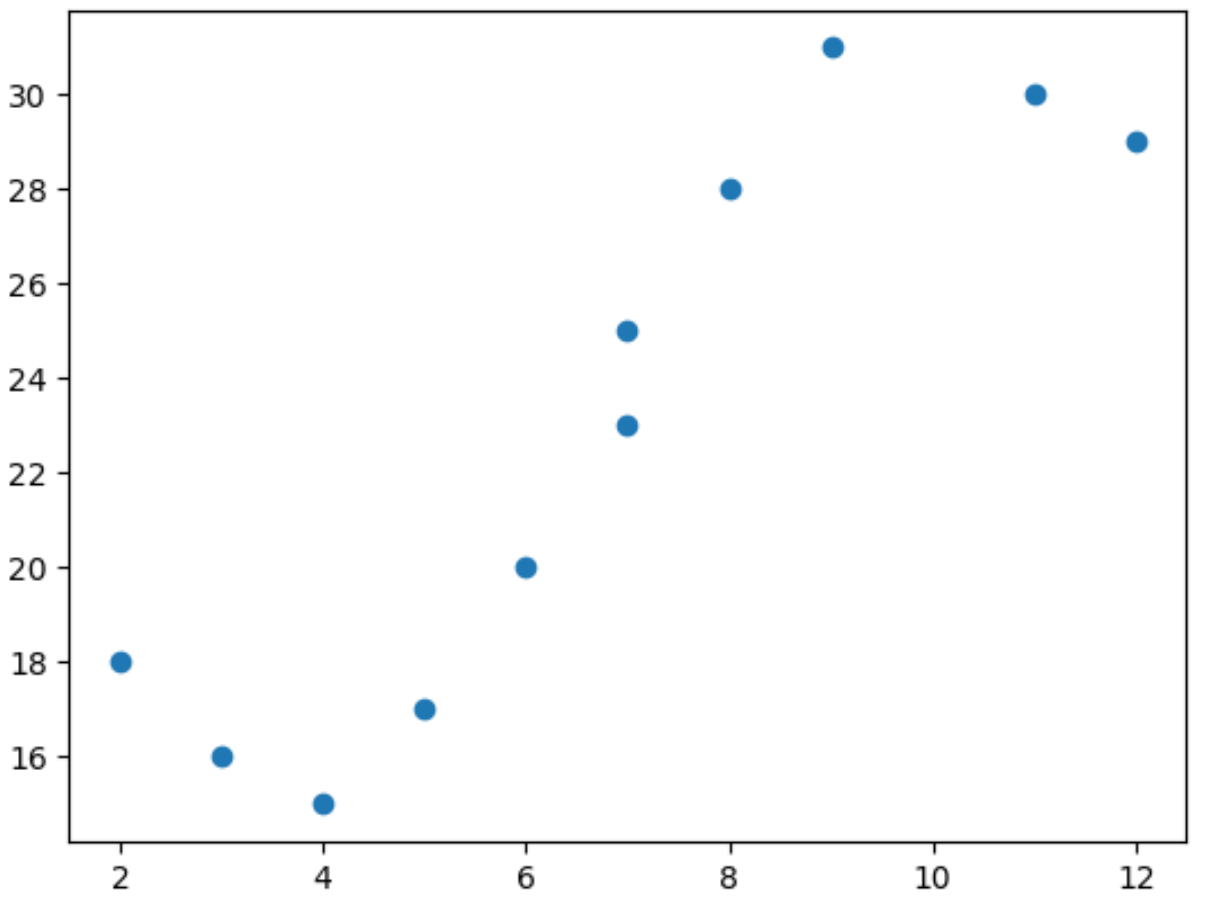
स्कैटरप्लॉट से, हम देख सकते हैं कि x और y के बीच संबंध रैखिक नहीं है।

इसलिए दो चरों के बीच गैर-रैखिक संबंध को पकड़ने के लिए डेटा में बहुपद प्रतिगमन मॉडल को फिट करना एक अच्छा विचार है।

चरण 2: बहुपद प्रतिगमन मॉडल को फ़िट करें

निम्नलिखित कोड दिखाता है कि इस डेटा सेट में डिग्री 3 बहुपद प्रतिगमन मॉडल को फिट करने के लिए स्केलेर फ़ंक्शंस का उपयोग कैसे करें:

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

अंतिम पंक्ति में दिखाए गए मॉडल गुणांकों का उपयोग करके, हम फिट किए गए बहुपद प्रतिगमन समीकरण को निम्नानुसार लिख सकते हैं:

y = -0.109x ³ + 2.256x ² – 11.839x + 33.626

इस समीकरण का उपयोग पूर्वानुमानित चर के दिए गए मान को देखते हुए प्रतिक्रिया चर के अपेक्षित मूल्य को खोजने के लिए किया जा सकता है।

उदाहरण के लिए, यदि x 4 है, तो प्रतिक्रिया चर, y के लिए अपेक्षित मान 15.39 होगा:

y = -0.109(4) ³ + 2.256(4) ² – 11.839(4) + 33.626= 15.39

ध्यान दें : एक बहुपद प्रतिगमन मॉडल को एक अलग डिग्री के साथ फिट करने के लिए, बस PolynomialFeatures() फ़ंक्शन में डिग्री तर्क का मान बदलें।

चरण 3: बहुपद प्रतिगमन मॉडल की कल्पना करें

अंत में, हम मूल डेटा बिंदुओं पर फिट किए गए बहुपद प्रतिगमन मॉडल की कल्पना करने के लिए एक सरल प्लॉट बना सकते हैं:

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

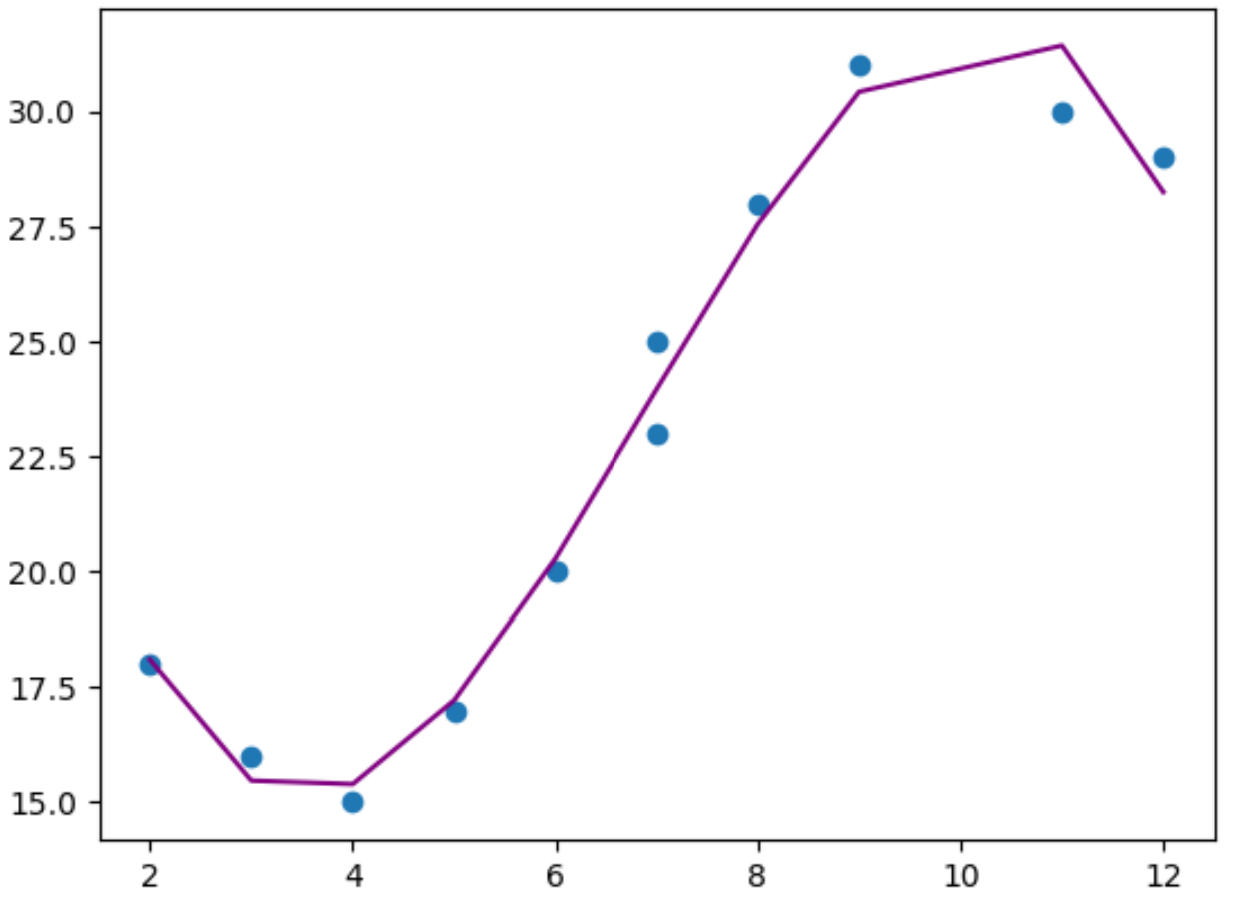
ग्राफ़ से, हम देख सकते हैं कि बहुपद प्रतिगमन मॉडल ओवरफिटिंग के बिना डेटा को अच्छी तरह से फिट करता है।

ध्यान दें : आप स्केलेर पॉलीनोमियलफीचर्स() फ़ंक्शन के लिए पूर्ण दस्तावेज़ यहां पा सकते हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि स्केलेरन का उपयोग करके अन्य सामान्य कार्य कैसे करें:

स्केलेरन से प्रतिगमन गुणांक कैसे निकालें
स्केलेर का उपयोग करके संतुलित परिशुद्धता की गणना कैसे करें
स्केलेरन में वर्गीकरण रिपोर्ट की व्याख्या कैसे करें