सरल रेखीय प्रतिगमन का परिचय

सरल रेखीय प्रतिगमन एक सांख्यिकीय पद्धति है जिसका उपयोग आप दो चर, x और y के बीच संबंध को समझने के लिए कर सकते हैं।

एक चर, x , को भविष्यवक्ता चर के रूप में जाना जाता है।

अन्य चर, y , को प्रतिक्रिया चर के रूप में जाना जाता है।

उदाहरण के लिए, मान लीजिए कि हमारे पास सात व्यक्तियों के वजन और ऊंचाई के साथ निम्नलिखित डेटासेट हैं:

वजन को पूर्वानुमानक चर होने दें और ऊँचाई को प्रतिक्रिया चर होने दें।

यदि हम एक्स-अक्ष पर वजन और वाई-अक्ष पर ऊंचाई के साथ स्कैटरप्लॉट का उपयोग करके इन दो चरों को ग्राफ़ करते हैं, तो यह इस तरह दिखेगा:

मान लीजिए हम वजन और ऊंचाई के बीच संबंध को समझना चाहते हैं। स्कैटरप्लॉट से हम स्पष्ट रूप से देख सकते हैं कि जैसे-जैसे वजन बढ़ता है, ऊंचाई भी बढ़ती है, लेकिन वास्तव में वजन और ऊंचाई के बीच इस संबंध को मापने के लिए हमें रैखिक प्रतिगमन का उपयोग करने की आवश्यकता होती है।

रैखिक प्रतिगमन का उपयोग करके, हम वह रेखा पा सकते हैं जो हमारे डेटा के लिए सबसे उपयुक्त “फिट” होती है। इस रेखा को न्यूनतम वर्ग प्रतिगमन रेखा के रूप में जाना जाता है और इसका उपयोग हमें वजन और ऊंचाई के बीच संबंधों को समझने में मदद करने के लिए किया जा सकता है।

आमतौर पर, आप इस पंक्ति के समीकरण को खोजने के लिए Microsoft Excel, SPSS, या ग्राफ़िंग कैलकुलेटर जैसे सॉफ़्टवेयर का उपयोग करेंगे।

सर्वोत्तम फ़िट की पंक्ति का सूत्र लिखा है:

ŷ = बी ₀ + बी ₁ एक्स

जहां ŷ प्रतिक्रिया चर का अनुमानित मूल्य है, बी ₀ अवरोधन है, बी ₁ प्रतिगमन गुणांक है, और एक्स भविष्यवक्ता चर का मूल्य है।

संबंधित: वास्तविक जीवन में रैखिक प्रतिगमन का उपयोग करने के 4 उदाहरण

“सर्वोत्तम उपयुक्त पंक्ति” ढूंढें

इस उदाहरण के लिए, हम बस अपने डेटा को सांख्यिकीय रैखिक प्रतिगमन कैलकुलेटर में प्लग कर सकते हैं और गणना दबा सकते हैं:

कैलकुलेटर स्वचालित रूप से न्यूनतम वर्ग प्रतिगमन रेखा ढूंढता है:

ŷ = 32.7830 + 0.2001x

यदि हम अपने पिछले स्कैटरप्लॉट से ज़ूम आउट करते हैं और इस पंक्ति को ग्राफ़ में जोड़ते हैं, तो यह इस तरह दिखेगा:

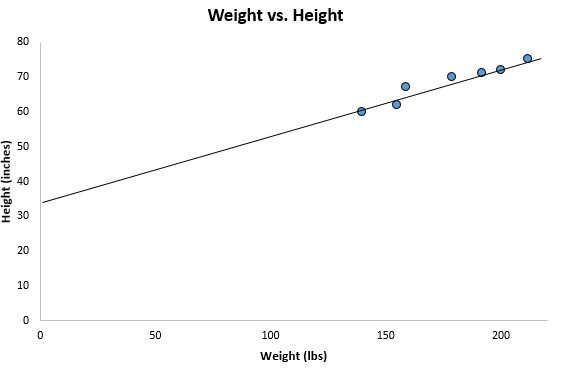
ध्यान दें कि कैसे हमारे डेटा बिंदु इस रेखा के चारों ओर बारीकी से बिखरे हुए हैं। वास्तव में, यह न्यूनतम वर्ग प्रतिगमन रेखा उन सभी संभावित रेखाओं में से हमारे डेटा के लिए सबसे उपयुक्त रेखा है जिसे हम खींच सकते हैं।

न्यूनतम वर्ग प्रतिगमन रेखा की व्याख्या कैसे करें

इस न्यूनतम वर्ग प्रतिगमन रेखा की व्याख्या इस प्रकार करें: ŷ = 32.7830 + 0.2001x

_बी0 = 32.7830 . इसका मतलब यह है कि जब भविष्यवक्ता चर वजन शून्य पाउंड है, तो अनुमानित ऊंचाई 32.7830 इंच है। कभी-कभी b ₀ का मान जानना उपयोगी हो सकता है, लेकिन इस विशिष्ट उदाहरण में b _{0 की} व्याख्या करने का कोई मतलब नहीं है क्योंकि कोई व्यक्ति शून्य पाउंड वजन नहीं कर सकता है।

_बी1 = 0.2001 । इसका मतलब यह है कि x में एक इकाई की वृद्धि y में 0.2001 इकाई की वृद्धि के साथ जुड़ी हुई है। इस मामले में, एक पाउंड वजन में वृद्धि 0.2001 इंच की ऊंचाई में वृद्धि के साथ जुड़ी हुई है।

न्यूनतम वर्ग समाश्रयण रेखा का उपयोग कैसे करें

इस न्यूनतम वर्ग समाश्रयण रेखा का उपयोग करके, हम जैसे प्रश्नों का उत्तर दे सकते हैं:

जिस व्यक्ति का वजन 170 पाउंड है, उससे हमें कितनी लंबाई की उम्मीद करनी चाहिए?

इस प्रश्न का उत्तर देने के लिए, हम बस x के लिए अपनी प्रतिगमन रेखा में 170 डाल सकते हैं और y के लिए हल कर सकते हैं:

ŷ = 32.7830 + 0.2001(170) = 66.8 इंच

150 पाउंड वजन वाले किसी व्यक्ति से हमें कितनी लंबाई की उम्मीद करनी चाहिए?

इस प्रश्न का उत्तर देने के लिए, हम x के लिए अपनी प्रतिगमन रेखा में 150 डाल सकते हैं और y के लिए हल कर सकते हैं:

ŷ = 32.7830 + 0.2001(150) = 62.798 इंच

सावधानी: इस तरह के प्रश्नों का उत्तर देने के लिए प्रतिगमन समीकरण का उपयोग करते समय, सुनिश्चित करें कि केवल भविष्यवक्ता चर के लिए उन मानों का उपयोग करें जो डेटा सेट में भविष्यवक्ता चर की सीमा के भीतर हैं। मूल जिसका उपयोग हमने न्यूनतम वर्ग प्रतिगमन रेखा उत्पन्न करने के लिए किया था। उदाहरण के लिए, हमारे डेटा सेट में वजन 140 और 212 पाउंड के बीच था। इसलिए जब वजन 140 और 212 पाउंड के बीच हो तो अपेक्षित ऊंचाई के बारे में सवालों का जवाब देना समझ में आता है।

निर्धारण का गुणांक

यह मापने का एक तरीका है कि न्यूनतम वर्ग प्रतिगमन रेखा डेटा को कितनी अच्छी तरह “फिट” करती है , निर्धारण के गुणांक का उपयोग करना है, जिसे आर ² दर्शाया गया है।

निर्धारण का गुणांक प्रतिक्रिया चर में भिन्नता का अनुपात है जिसे भविष्यवक्ता चर द्वारा समझाया जा सकता है।

निर्धारण का गुणांक 0 से 1 तक भिन्न हो सकता है। 0 का मान इंगित करता है कि प्रतिक्रिया चर को भविष्यवक्ता चर द्वारा बिल्कुल भी समझाया नहीं जा सकता है। 1 का मान इंगित करता है कि प्रतिक्रिया चर को भविष्यवक्ता चर द्वारा त्रुटि के बिना पूरी तरह से समझाया जा सकता है।

0 और 1 के बीच एक आर ² इंगित करता है कि प्रतिक्रिया चर को भविष्यवक्ता चर द्वारा किस हद तक समझाया जा सकता है। उदाहरण के लिए, 0.2 का आर ² इंगित करता है कि प्रतिक्रिया चर में 20% भिन्नता को भविष्यवक्ता चर द्वारा समझाया जा सकता है; 0.77 का आर ² इंगित करता है कि प्रतिक्रिया चर में 77% भिन्नता को भविष्यवक्ता चर द्वारा समझाया जा सकता है।

ध्यान दें कि हमारे पिछले परिणाम में हमने 0.9311 का आर ² प्राप्त किया था, जो इंगित करता है कि ऊंचाई में 93.11% परिवर्तनशीलता को वजन पूर्वानुमानक चर द्वारा समझाया जा सकता है:

इससे हमें पता चलता है कि वजन ऊंचाई का एक बहुत अच्छा संकेतक है।

रैखिक प्रतिगमन धारणाएँ

एक रेखीय प्रतिगमन मॉडल के परिणाम वैध और विश्वसनीय होने के लिए, हमें यह सत्यापित करना होगा कि निम्नलिखित चार धारणाएँ पूरी होती हैं:

1. रैखिक संबंध: स्वतंत्र चर, x और आश्रित चर, y के बीच एक रैखिक संबंध होता है।

2. स्वतंत्रता: अवशिष्ट स्वतंत्र होते हैं। विशेष रूप से, समय श्रृंखला डेटा में लगातार अवशेषों के बीच कोई संबंध नहीं है।

3. समरूपता: x के प्रत्येक स्तर पर अवशेषों में निरंतर भिन्नता होती है।

4. सामान्यता: मॉडल अवशेष सामान्य रूप से वितरित होते हैं।

यदि इनमें से एक या अधिक धारणाएँ पूरी नहीं होती हैं, तो हमारे रैखिक प्रतिगमन के परिणाम अविश्वसनीय या भ्रामक भी हो सकते हैं।

प्रत्येक धारणा की व्याख्या के लिए इस लेख का संदर्भ लें, यह कैसे निर्धारित करें कि धारणा पूरी हो गई है या नहीं, और यदि धारणा पूरी नहीं हुई तो क्या करें।