एसएएस में बॉक्स-कॉक्स परिवर्तन कैसे करें

बॉक्स-कॉक्स ट्रांसफ़ॉर्मेशन एक गैर-सामान्य रूप से वितरित डेटा सेट को अधिक सामान्य रूप से वितरित सेट में बदलने के लिए आमतौर पर इस्तेमाल की जाने वाली विधि है।

इस पद्धति के पीछे मूल विचार निम्नलिखित सूत्र का उपयोग करके λ के लिए एक मान ज्ञात करना है, ताकि रूपांतरित डेटा यथासंभव सामान्य वितरण के करीब हो:

• y(λ) = (y ^λ – 1) / λ यदि y ≠ 0
• y(λ) = लॉग(y) यदि y = 0

हम PROC ट्रांसरेग प्रक्रिया का उपयोग करके एसएएस में λ के लिए उपयोग करने के लिए इष्टतम मूल्य की पहचान कर सकते हैं।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में इस प्रक्रिया का उपयोग कैसे करें।

उदाहरण: एसएएस में बॉक्स-कॉक्स परिवर्तन

आइए मान लें कि हमारे पास एसएएस में निम्नलिखित डेटा सेट है:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
7 1
7 1
8 1
3 2
2 2
4 2
4 2
6 2
6 2
7 3
5 3
3 3
3 6
5 7
8 8
;
run;

/*view dataset*/
proc print data =my_data;

मान लीजिए कि हम इस डेटा सेट में एक सरल रैखिक प्रतिगमन मॉडल को फिट करने के लिए PROC REG का उपयोग करते हैं, जिसमें x को पूर्वसूचक चर के रूप में और y को प्रतिक्रिया चर के रूप में उपयोग किया जाता है।

 /*fit simple linear regression model*/
proc reg data =my_data;
    model y = x;
run ;

आउटपुट डायग्नोस्टिक प्लॉट्स में, हम यह देखने के लिए अवशिष्ट बनाम क्वांटाइल प्लॉट (मध्य पंक्ति में सबसे बाईं ओर का प्लॉट) प्रदर्शित कर सकते हैं कि क्या अवशेष मॉडल में लगभग सामान्य रूप से वितरित हैं:

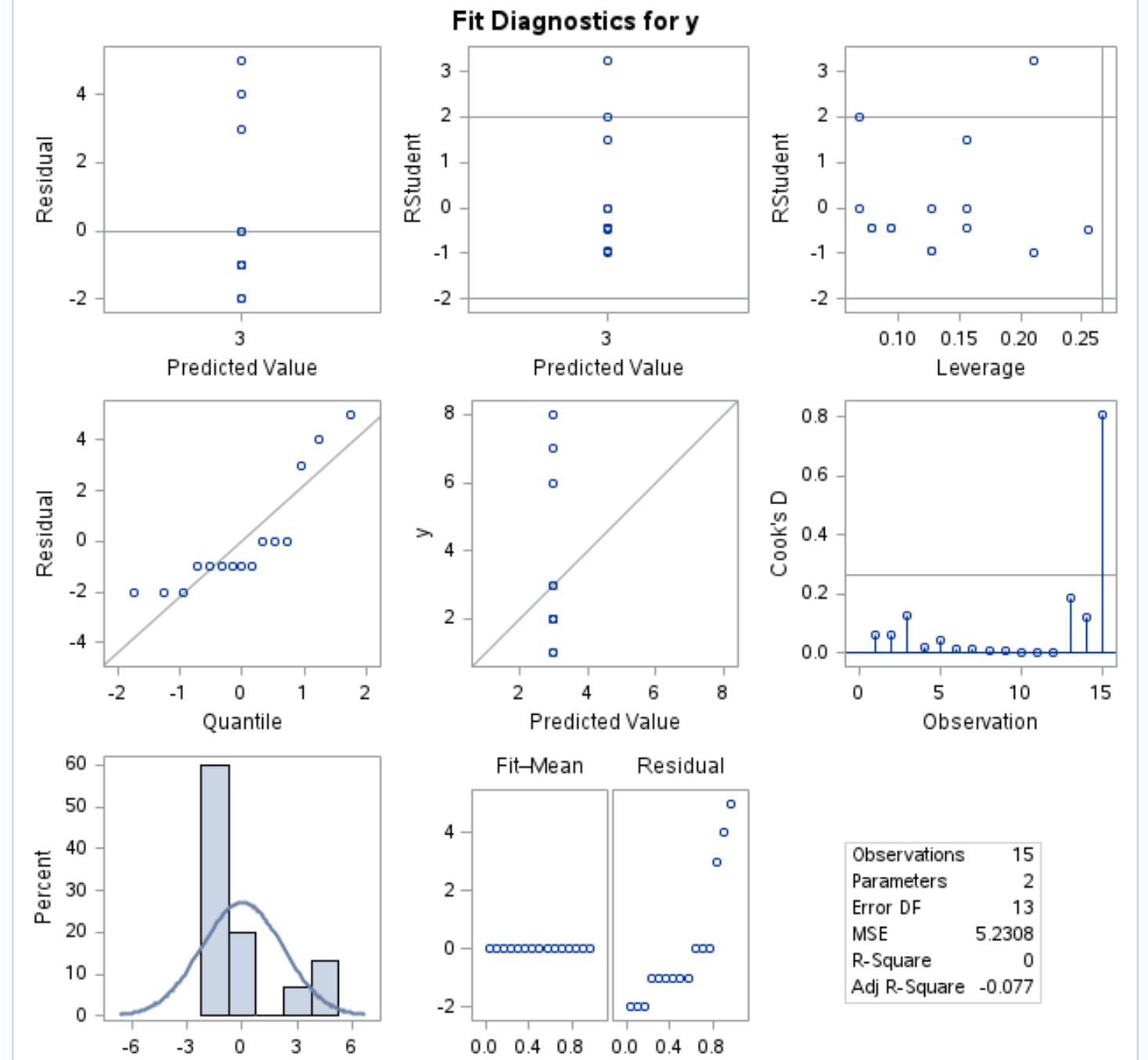
यदि अवशेष ग्राफ़ की दाहिनी विकर्ण रेखा के लगभग स्थित हैं, तो हम आम तौर पर मानते हैं कि अवशेष सामान्य रूप से वितरित हैं।

ग्राफ़ से हम देख सकते हैं कि अवशेष सीधी विकर्ण रेखा का बहुत अधिक अनुसरण नहीं करते हैं।

यह इंगित करता है कि प्रतिगमन मॉडल में प्रतिक्रिया चर सामान्य रूप से वितरित नहीं होने की संभावना है।

चूँकि प्रतिक्रिया चर सामान्य रूप से वितरित नहीं होता है, हम λ के मान की पहचान करने के लिए PROC TRANSREG का उपयोग कर सकते हैं जिसका उपयोग हम प्रतिक्रिया चर को बदलने के लिए कर सकते हैं ताकि यह अधिक सामान्य रूप से वितरित हो:

 /*perform box-cox transformation*/
proc transreg data =my_data;
    model boxcox (y) = identity (x);
run ;

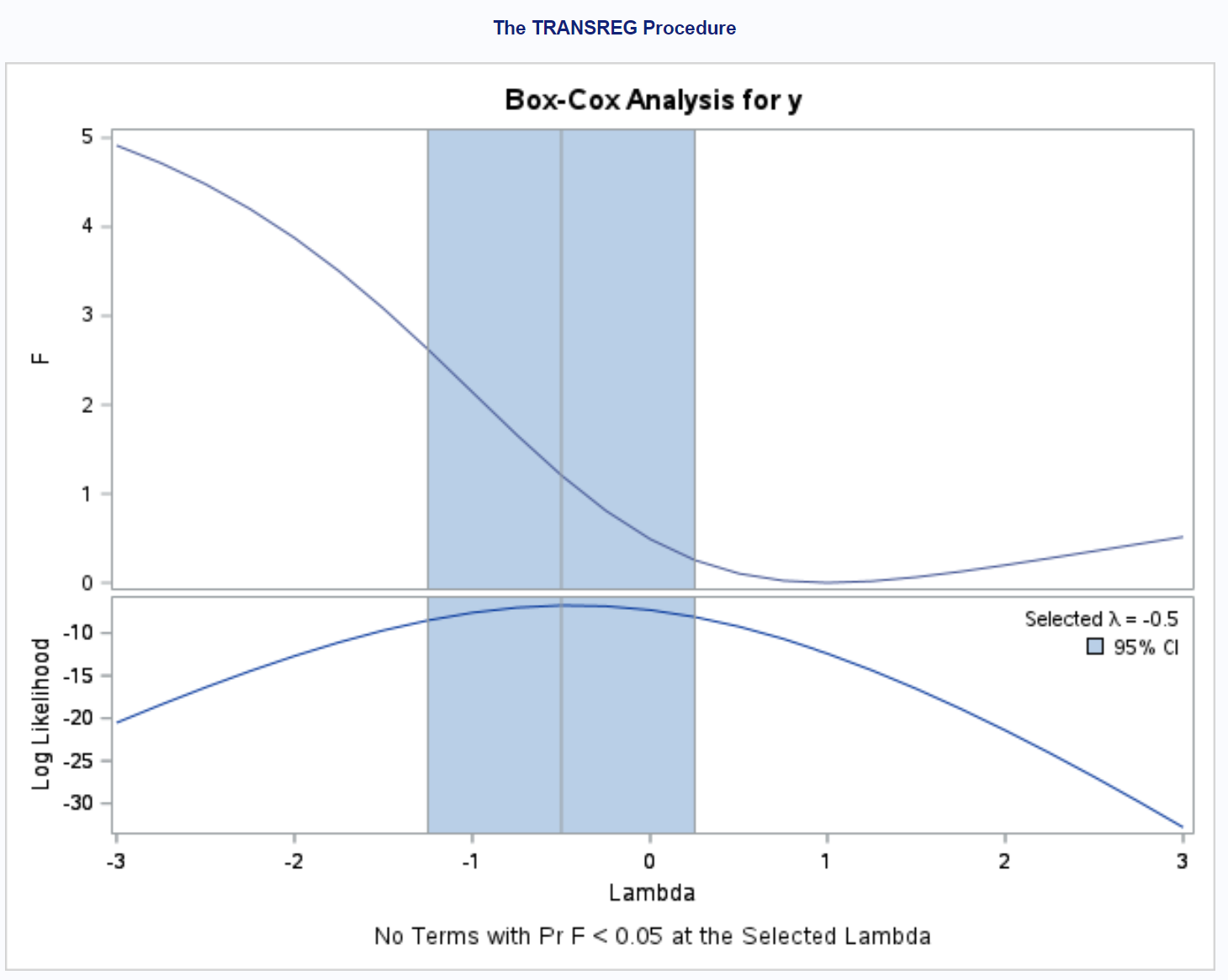
आउटपुट हमें बताता है कि λ के लिए उपयोग करने के लिए चयनित मान – 0.5 है।

इस प्रकार, हम मूल प्रतिक्रिया चर y को चर y = (y ^-0.5 – 1) / -0.5 के साथ प्रतिस्थापित करके एक सरल रैखिक प्रतिगमन मॉडल फिट कर सकते हैं।

निम्नलिखित कोड दिखाता है कि यह कैसे करना है:

 /*create new dataset that uses box-cox transformation to create new y*/
data new_data;
   set my_data;
   new_y = (y**(-0.5) - 1) / -0.5;
run ;

/*fit simple linear regression model using new response variable*/
proc reg data =new_data;
    model new_y = x;
run ;

अवशिष्ट बनाम में इस मॉडल के आउटपुट के क्वांटाइल प्लॉट में , हम देख सकते हैं कि अवशेष सीधी विकर्ण रेखा के साथ अधिक निकटता से स्थित हैं:

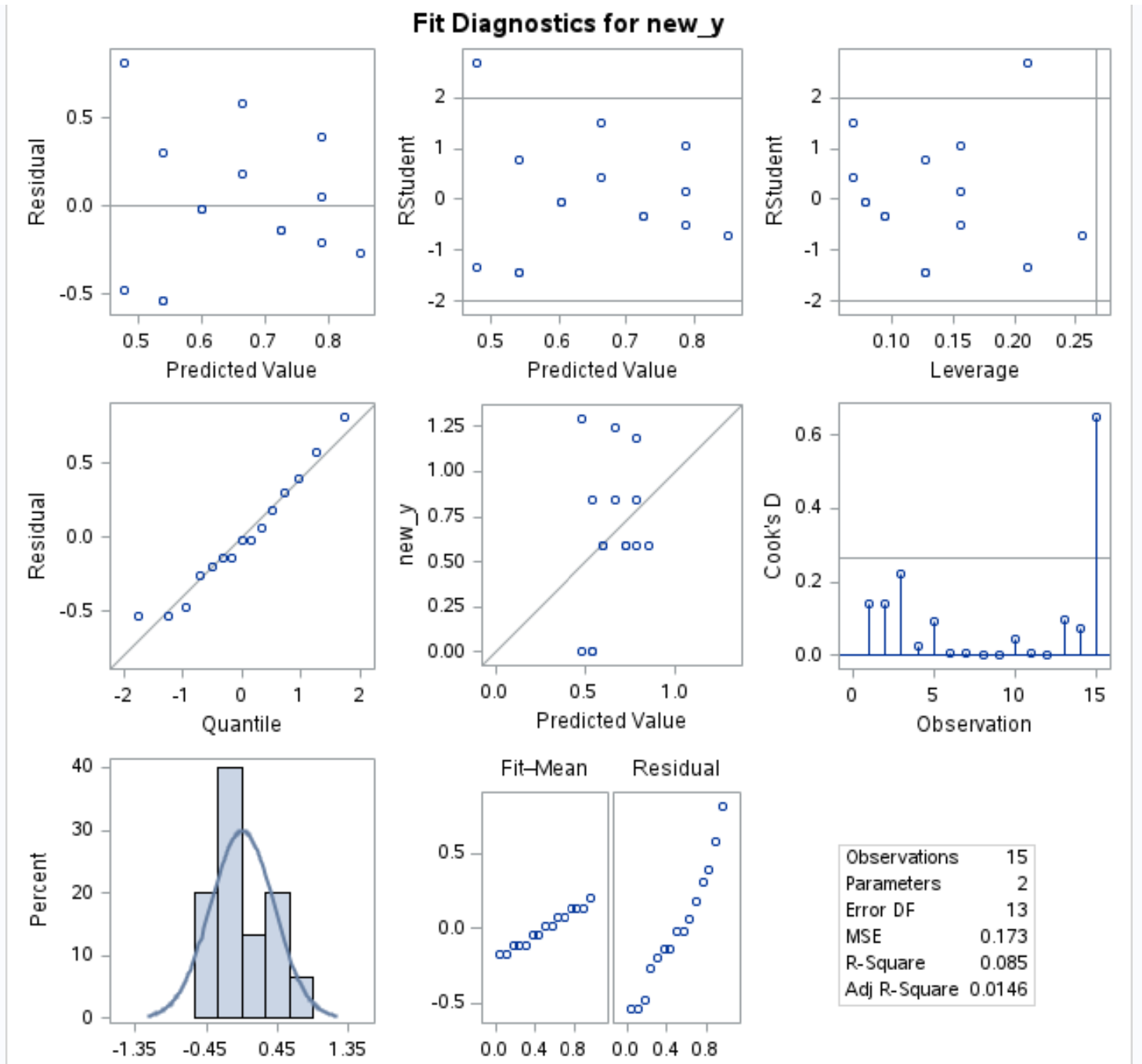
यह इंगित करता है कि बॉक्स-कॉक्स रूपांतरित मॉडल के अवशेष अधिक सामान्य रूप से वितरित हैं, जो रैखिक प्रतिगमन की मुख्य मान्यताओं में से एक को संतुष्ट करता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एसएएस में अन्य सामान्य कार्य कैसे करें:

एसएएस में सामान्यता परीक्षण के लिए प्रोक यूनीवेरिएट का उपयोग कैसे करें
एसएएस में एक अवशिष्ट प्लॉट कैसे बनाएं
एसएएस में लेवेने परीक्षण कैसे करें