सहप्रसरण मैट्रिक्स कैसे पढ़ें

सहप्रसरण इस बात का माप है कि एक चर में परिवर्तन दूसरे चर में परिवर्तन से कैसे जुड़े हैं। अधिक विशेष रूप से, यह उस डिग्री का माप है जिससे दो चर रैखिक रूप से जुड़े हुए हैं।

सहप्रसरण मैट्रिक्स एक वर्ग मैट्रिक्स है जो कई अलग-अलग चरों के बीच सहप्रसरण को दर्शाता है। यह समझने का एक उपयोगी तरीका हो सकता है कि डेटा सेट में विभिन्न चर कैसे संबंधित हैं।

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में सहप्रसरण मैट्रिक्स को कैसे पढ़ा जाए।

सहप्रसरण मैट्रिक्स कैसे पढ़ें

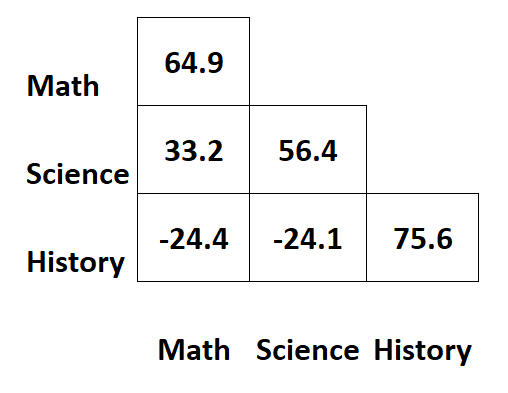
मान लीजिए कि हमारे पास निम्नलिखित सहप्रसरण मैट्रिक्स है जिसमें छात्रों के लिए तीन अलग-अलग विषयों के परीक्षा अंकों के बारे में जानकारी है:

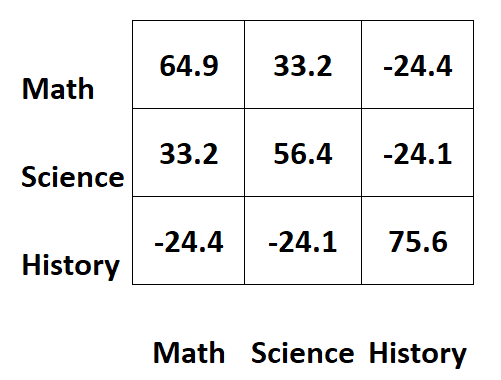
मैट्रिक्स के विकर्णों के साथ मान प्रत्येक विषय के भिन्नताओं का प्रतिनिधित्व करते हैं।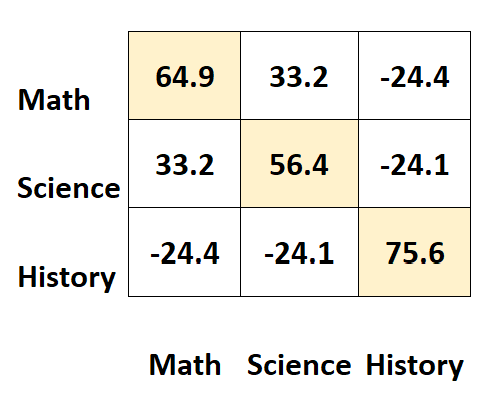

उदाहरण के लिए:

• गणित के परिणामों का प्रसरण 64.9 है।
• विज्ञान के अंकों का अंतर 56.4 है।
• ऐतिहासिक अंकों का विचरण 75.6 है।

मैट्रिक्स के अन्य मान विभिन्न विषयों के बीच सहप्रसरण का प्रतिनिधित्व करते हैं।

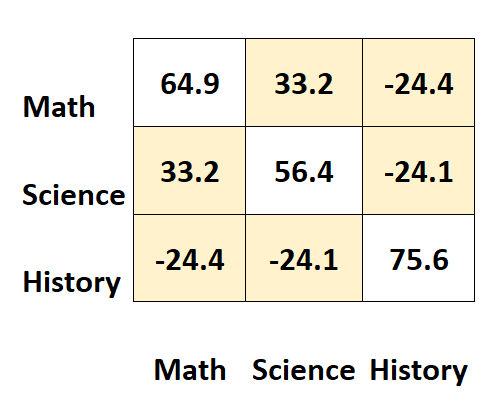
उदाहरण के लिए:

• गणित और विज्ञान के अंकों के बीच सहप्रसरण 33.2 है।
• गणित और इतिहास के अंकों के बीच सहप्रसरण -24.4 है।
• विज्ञान और इतिहास के अंकों के बीच सहप्रसरण -24.1 है।

सहप्रसरण के लिए एक सकारात्मक संख्या इंगित करती है कि दो चर एक साथ बढ़ने या घटने की प्रवृत्ति रखते हैं।

उदाहरण के लिए, गणित और विज्ञान में एक सकारात्मक सहप्रसरण ( 33.2 ) है, जो दर्शाता है कि जो छात्र गणित में उच्च अंक प्राप्त करते हैं, वे विज्ञान में भी उच्च अंक प्राप्त करते हैं।

इसके विपरीत, जो छात्र गणित में खराब प्रदर्शन करते हैं, वे विज्ञान में भी खराब प्रदर्शन करते हैं।

सहप्रसरण के लिए एक ऋणात्मक संख्या इंगित करती है कि जैसे-जैसे एक चर बढ़ता है, दूसरा चर घटता जाता है।

उदाहरण के लिए, गणित और इतिहास में नकारात्मक सहप्रसरण ( -24.44 ) है, जो दर्शाता है कि जो छात्र गणित में अच्छा प्रदर्शन करते हैं, वे इतिहास में कम प्रदर्शन करते हैं।

इसके विपरीत, जो छात्र गणित में कम अंक प्राप्त करते हैं वे इतिहास में उच्च अंक प्राप्त करते हैं।

सहप्रसरण मैट्रिक्स की समरूपता पर एक नोट

यह ध्यान दिया जाना चाहिए कि एक सहप्रसरण मैट्रिक्स पूरी तरह से सममित है।

उदाहरण के लिए, शीर्ष दाएँ कक्ष बिल्कुल वही मान दिखाता है जो नीचे बाएँ कक्ष में है:

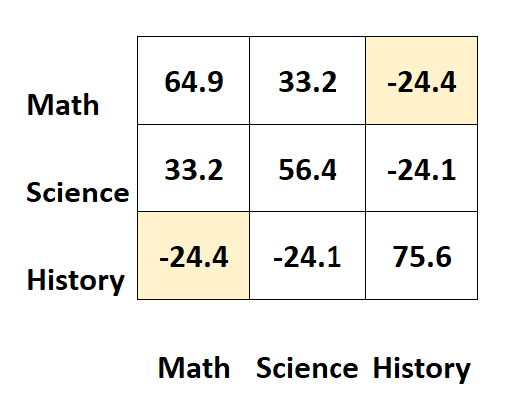
दरअसल, दो कोशिकाएं इतिहास और गणित के बीच सहप्रसरण को मापती हैं।

चूँकि सहप्रसरण मैट्रिक्स सममित है, मैट्रिक्स में प्रदर्शित सहप्रसरण मानों में से आधे निरर्थक और अनावश्यक हैं।

इसलिए, कभी-कभी सहप्रसरण मैट्रिक्स का केवल आधा हिस्सा ही प्रदर्शित किया जाएगा:

सहप्रसरण मैट्रिक्स का उपयोग कब करें

व्यवहार में, आपको सहप्रसरण मैट्रिक्स की तुलना में अक्सर सहसंबंध मैट्रिक्स बनाने और व्याख्या करने की आवश्यकता होगी।

हालाँकि, विभिन्न मशीन लर्निंग एल्गोरिदम और मॉडल के लिए सहप्रसरण मैट्रिक्स का उपयोग अक्सर “हुड के नीचे” किया जाता है।

उदाहरण के लिए, सहप्रसरण मैट्रिक्स का उपयोग प्रमुख घटकों के विश्लेषण के दौरान किया जाता है, जो हमें बड़ी संख्या में चर वाले डेटा सेट में अंतर्निहित पैटर्न को समझने में मदद करता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर का उपयोग करके सहप्रसरण मैट्रिक्स कैसे बनाया जाए:

आर में सहप्रसरण मैट्रिक्स कैसे बनाएं
पायथन में कोवरियन्स मैट्रिक्स कैसे बनाएं
एसपीएसएस में कोवरियन्स मैट्रिक्स कैसे बनाएं
एक्सेल में कोवरियन्स मैट्रिक्स कैसे बनाएं