एसएएस में प्रमुख घटक विश्लेषण कैसे करें

प्रिंसिपल कंपोनेंट एनालिसिस (पीसीए) एक अप्रशिक्षित मशीन लर्निंग तकनीक है जो प्रमुख घटकों – भविष्यवक्ता चर के रैखिक संयोजन – को खोजने का प्रयास करती है जो डेटा सेट में भिन्नता के एक बड़े हिस्से की व्याख्या करते हैं।

एसएएस में पीसीए करने का सबसे सरल तरीका PROC PRINCOMP स्टेटमेंट का उपयोग करना है, जो निम्नलिखित मूल सिंटैक्स का उपयोग करता है:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

यहां बताया गया है कि प्रत्येक निर्देश क्या करता है:

• डेटा : पीसीए के लिए उपयोग किए जाने वाले डेटासेट का नाम
• आउट : बनाए जाने वाले डेटासेट का नाम जिसमें सभी मूल डेटा और प्रमुख घटक स्कोर शामिल हैं
• आउटस्टैट : निर्दिष्ट करता है कि एक डेटा सेट बनाया जाना चाहिए जिसमें साधन, मानक विचलन, सहसंबंध गुणांक, आइगेनवैल्यू और आइजेनवेक्टर शामिल हों।
• var : इनपुट डेटासेट से पीसीए के लिए उपयोग किए जाने वाले वेरिएबल।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि एसएएस में प्रमुख घटकों का विश्लेषण करने के लिए व्यवहार में PROC PRINCOMP कथन का उपयोग कैसे करें।

चरण 1: एक डेटासेट बनाएं

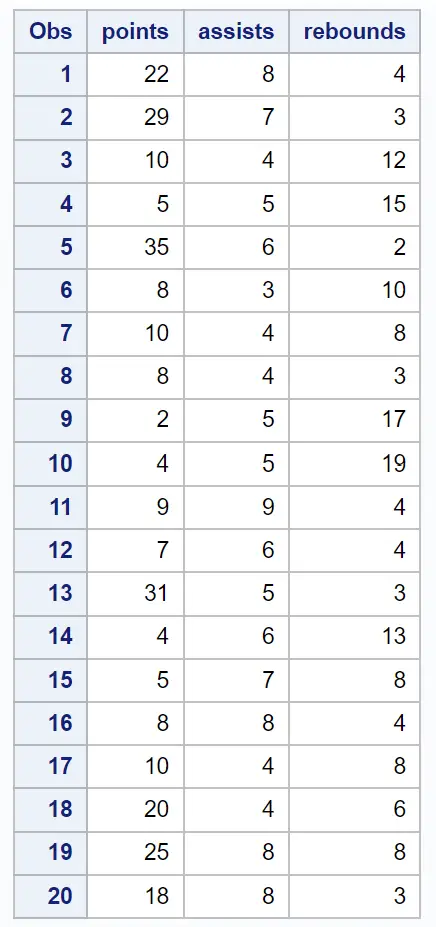
मान लीजिए कि हमारे पास निम्नलिखित डेटासेट है जिसमें 20 बास्केटबॉल खिलाड़ियों के बारे में विभिन्न जानकारी है:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

चरण 2: प्रमुख घटकों का विश्लेषण करें

हम डेटासेट के पॉइंट्स , असिस्ट और बाउंस वेरिएबल्स का उपयोग करके प्रमुख घटक विश्लेषण करने के लिए PROC PRINCOMP स्टेटमेंट का उपयोग कर सकते हैं:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

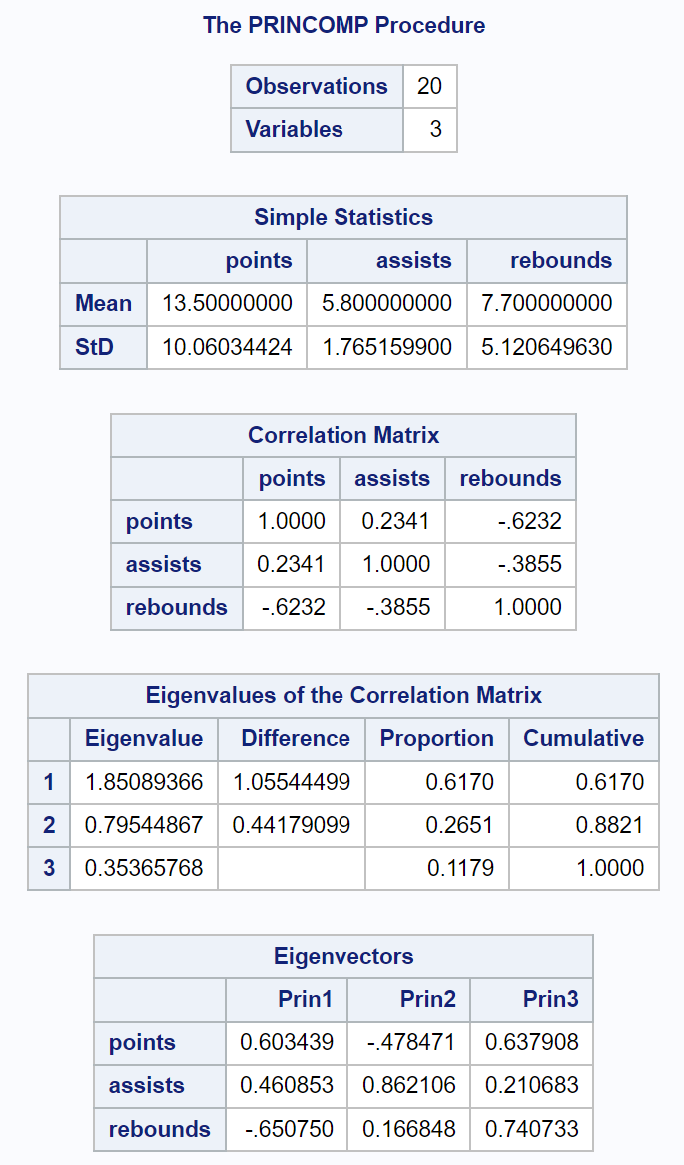
आउटपुट का पहला भाग विभिन्न वर्णनात्मक आँकड़े प्रदर्शित करता है, जिसमें प्रत्येक इनपुट चर का माध्य और मानक विचलन, एक सहसंबंध मैट्रिक्स, और eigenvalues और eigenvectors के मान शामिल हैं:

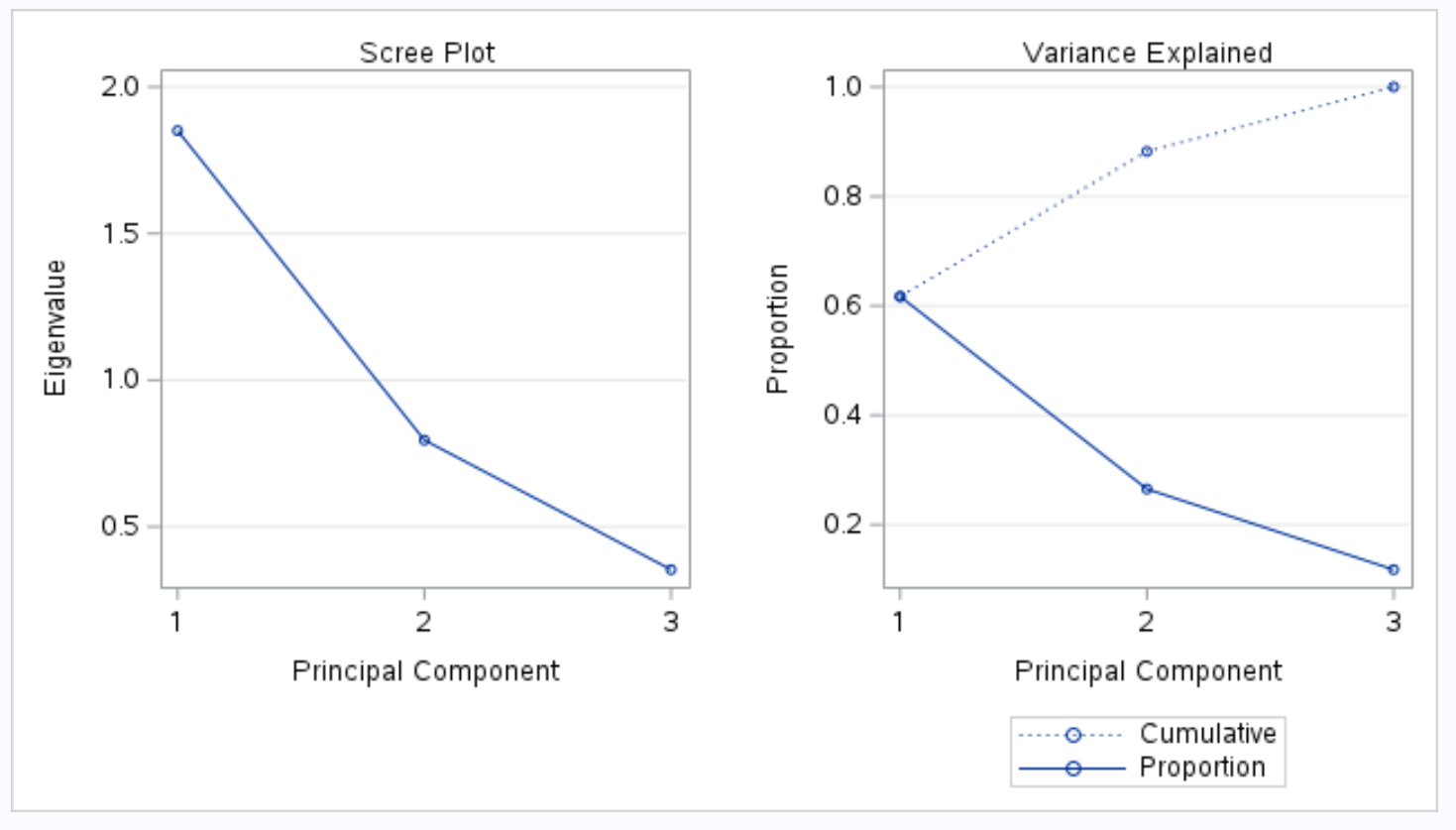
आउटपुट का अगला भाग एक डरावना प्लॉट और एक समझाया हुआ विचरण प्लॉट प्रदर्शित करता है:

जब हम पीसीए करते हैं, तो हम अक्सर यह समझना चाहते हैं कि डेटा सेट में कुल भिन्नता का कितना प्रतिशत प्रत्येक प्रमुख घटक द्वारा समझाया जा सकता है।

सहसंबंध मैट्रिक्स आइगेनवैल्यू शीर्षक वाली परिणामी तालिका हमें यह देखने की अनुमति देती है कि प्रत्येक प्रमुख घटक द्वारा कुल भिन्नता का कितना प्रतिशत समझाया गया है:

• पहला प्रमुख घटक डेटासेट में कुल भिन्नता का 61.7% बताता है।
• दूसरा प्रमुख घटक डेटासेट में कुल भिन्नता का 26.51% बताता है।
• तीसरा प्रमुख घटक डेटासेट में कुल भिन्नता का 11.79% बताता है।

ध्यान दें कि सभी प्रतिशतों का योग 100% होता है।

वेरिएंस एक्सप्लेन्ड शीर्षक वाला कथानक हमें इन मूल्यों की कल्पना करने की अनुमति देता है।

x-अक्ष प्रमुख घटक को प्रदर्शित करता है और y-अक्ष प्रत्येक व्यक्तिगत प्रमुख घटक द्वारा समझाए गए कुल विचरण का प्रतिशत प्रदर्शित करता है।

चरण 3: परिणामों की कल्पना करने के लिए एक बाइप्लॉट बनाएं

किसी दिए गए डेटासेट के लिए पीसीए के परिणामों की कल्पना करने के लिए, हम एक बाइप्लॉट बना सकते हैं, जो एक प्लॉट है जो पहले दो प्रमुख घटकों द्वारा गठित एक विमान पर डेटासेट में प्रत्येक अवलोकन को प्रदर्शित करता है।

हम बाइप्लॉट बनाने के लिए एसएएस में निम्नलिखित सिंटैक्स का उपयोग कर सकते हैं:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

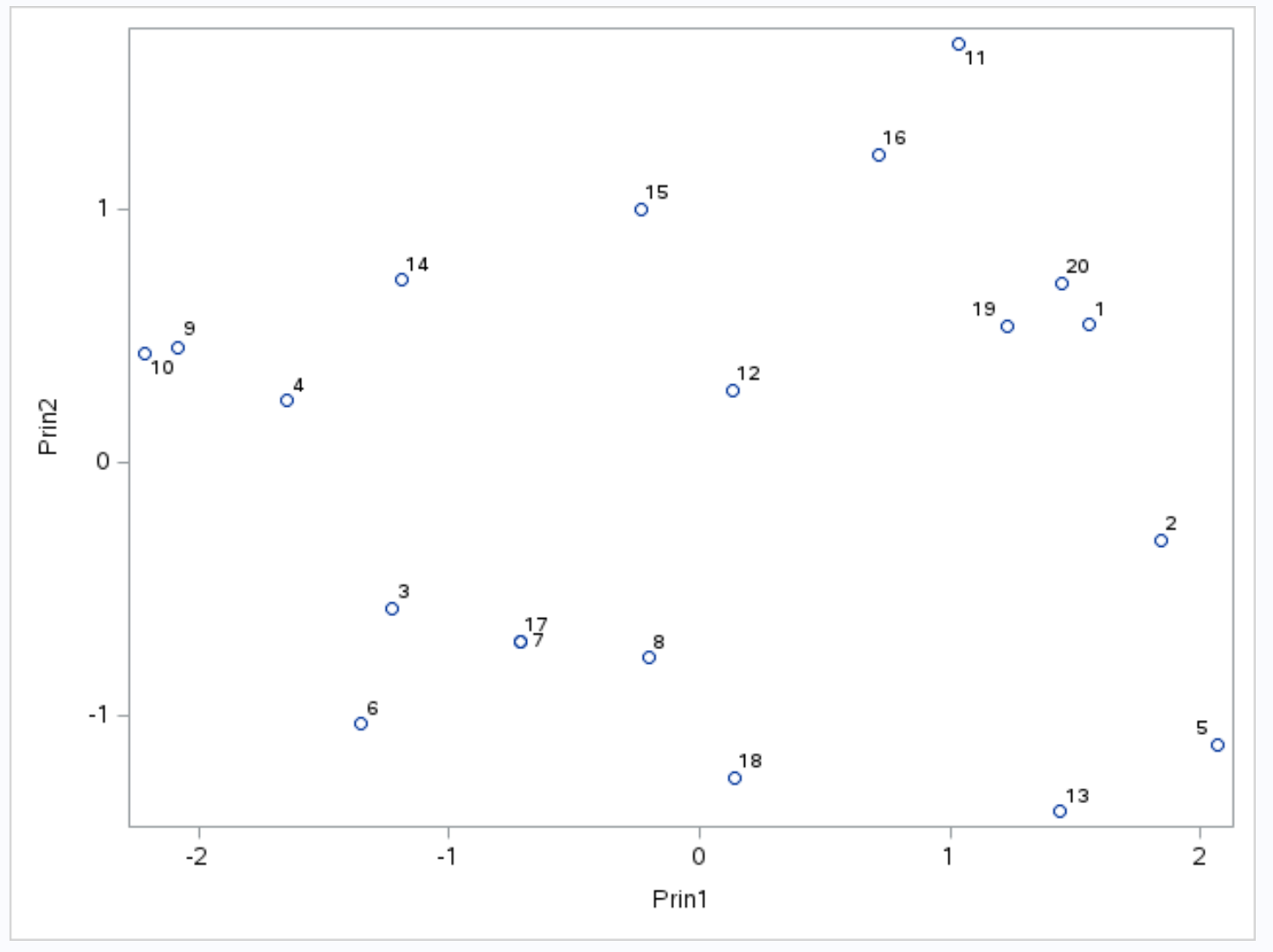
x-अक्ष पहला प्रमुख घटक प्रदर्शित करता है, y-अक्ष दूसरा प्रमुख घटक प्रदर्शित करता है, और डेटासेट से व्यक्तिगत अवलोकन ग्राफ़ के अंदर छोटे वृत्तों के रूप में प्रदर्शित होते हैं।

ग्राफ़ पर साथ-साथ मौजूद अवलोकनों में अंक , सहायता और रिबाउंड के तीन चर के लिए समान मान होते हैं।

उदाहरण के लिए, ग्राफ़ के सबसे बाईं ओर, हम देख सकते हैं कि अवलोकन #9 और #10 एक-दूसरे के बेहद करीब हैं।

यदि हम मूल डेटासेट का संदर्भ लें, तो हम इन अवलोकनों के लिए निम्नलिखित मान देख सकते हैं:

• अवलोकन संख्या 9 : 2 अंक, 5 सहायता, 17 रिबाउंड
• अवलोकन #10 : 4 अंक, 5 सहायता, 19 रिबाउंड

तीनों चरों में से प्रत्येक के लिए मान समान हैं, जो बताता है कि ये अवलोकन बाइप्लॉट पर एक-दूसरे के इतने करीब क्यों हैं।

हमने सहसंबंध मैट्रिक्स आइगेनवैल्यू शीर्षक वाली परिणाम तालिका में यह भी देखा कि पहले दो प्रमुख घटक डेटासेट में कुल भिन्नता का 88.21% हिस्सा हैं।

चूँकि यह प्रतिशत बहुत अधिक है, इसलिए यह विश्लेषण करना वैध है कि बाइप्लॉट में कौन से अवलोकन एक-दूसरे के करीब हैं, क्योंकि बाइप्लॉट बनाने वाले दो प्रमुख घटक डेटासेट में लगभग सभी भिन्नताओं के लिए जिम्मेदार हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एसएएस में अन्य सामान्य कार्य कैसे करें:

एसएएस में सरल रैखिक प्रतिगमन कैसे करें
एसएएस में मल्टीपल लीनियर रिग्रेशन कैसे करें
एसएएस में लॉजिस्टिक रिग्रेशन कैसे करें