रैखिक प्रतिगमन की चार धारणाएँ

रैखिक प्रतिगमन एक उपयोगी सांख्यिकीय पद्धति है जिसका उपयोग हम दो चर, x और y के बीच संबंध को समझने के लिए कर सकते हैं। हालाँकि, एक रेखीय प्रतिगमन करने से पहले, हमें पहले यह सुनिश्चित करना होगा कि चार धारणाएँ पूरी हों:

1. रैखिक संबंध: स्वतंत्र चर, x और आश्रित चर, y के बीच एक रैखिक संबंध होता है।

2. स्वतंत्रता: अवशिष्ट स्वतंत्र होते हैं। विशेष रूप से, समय श्रृंखला डेटा में लगातार अवशेषों के बीच कोई संबंध नहीं है।

3. समरूपता: x के प्रत्येक स्तर पर अवशेषों में निरंतर भिन्नता होती है।

4. सामान्यता: मॉडल अवशेष सामान्य रूप से वितरित होते हैं।

यदि इनमें से एक या अधिक धारणाएँ पूरी नहीं होती हैं, तो हमारे रैखिक प्रतिगमन के परिणाम अविश्वसनीय या भ्रामक भी हो सकते हैं।

इस लेख में, हम प्रत्येक धारणा के लिए एक स्पष्टीकरण प्रदान करते हैं, यह कैसे निर्धारित किया जाए कि धारणा पूरी हो गई है या नहीं, और यदि धारणा पूरी नहीं हुई है तो क्या करें।

परिकल्पना 1: रैखिक संबंध

स्पष्टीकरण

रैखिक प्रतिगमन की पहली धारणा यह है कि स्वतंत्र चर x और स्वतंत्र चर y के बीच एक रैखिक संबंध है।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह पता लगाने का सबसे आसान तरीका है कि यह धारणा संतुष्ट है या नहीं, x बनाम y का स्कैटरप्लॉट बनाना है। यह आपको स्पष्ट रूप से यह देखने की अनुमति देता है कि क्या दो चरों के बीच कोई रैखिक संबंध है। यदि ऐसा प्रतीत होता है कि प्लॉट पर बिंदु एक सीधी रेखा पर स्थित हो सकते हैं, तो दो चर के बीच कुछ प्रकार का रैखिक संबंध होता है और यह धारणा पूरी होती है।

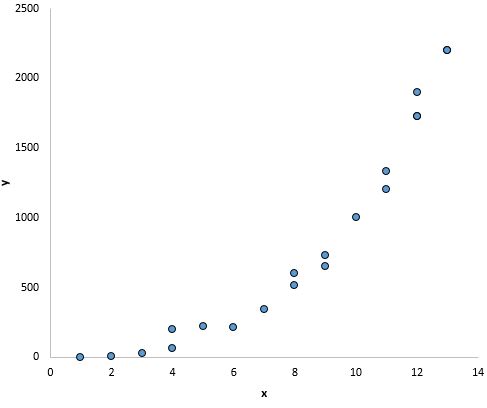
उदाहरण के लिए, नीचे दिए गए ग्राफ़ में बिंदु एक सीधी रेखा पर पड़ते प्रतीत होते हैं, जो दर्शाता है कि x और y के बीच एक रैखिक संबंध है:

हालाँकि, नीचे दिए गए ग्राफ़ में x और y के बीच कोई रैखिक संबंध नहीं दिखता है:

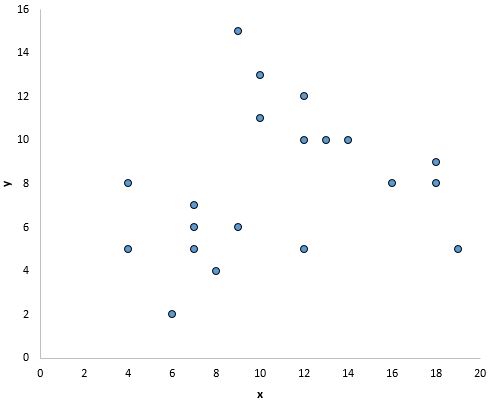
और इस ग्राफ़ में, x और y के बीच एक स्पष्ट संबंध प्रतीत होता है, लेकिन एक रैखिक संबंध नहीं :

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि आप x और y के लिए मानों का एक स्कैटरप्लॉट बनाते हैं और पाते हैं कि दोनों चरों के बीच कोई रैखिक संबंध नहीं है, तो आपके पास कई विकल्प हैं:

1. स्वतंत्र और/या आश्रित चर पर एक अरेखीय परिवर्तन लागू करें। सामान्य उदाहरणों में स्वतंत्र और/या आश्रित चर का लॉग, वर्गमूल, या व्युत्क्रम लेना शामिल है।

2. मॉडल में एक और स्वतंत्र चर जोड़ें। उदाहरण के लिए, यदि x बनाम y के प्लॉट में एक परवलयिक आकार है, तो मॉडल में एक अतिरिक्त स्वतंत्र चर के रूप में X ² जोड़ने का अर्थ हो सकता है।

परिकल्पना 2: स्वतंत्रता

स्पष्टीकरण

रैखिक प्रतिगमन की अगली धारणा यह है कि अवशेष स्वतंत्र हैं। समय श्रृंखला डेटा के साथ काम करते समय यह विशेष रूप से प्रासंगिक है। आदर्श रूप से, हम नहीं चाहते कि लगातार अवशेषों के बीच कोई प्रवृत्ति हो। उदाहरण के लिए, समय के साथ अवशेष लगातार नहीं बढ़ने चाहिए।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह धारणा कायम है या नहीं, इसका परीक्षण करने का सबसे सरल तरीका अवशिष्टों के समय श्रृंखला प्लॉट को देखना है, जो समय बनाम अवशिष्टों का प्लॉट है। आदर्श रूप से, अधिकांश अवशिष्ट ऑटोसहसंबंध शून्य के आसपास 95% विश्वास बैंड के भीतर आने चाहिए, जो n के वर्गमूल पर लगभग +/- 2 स्थित हैं, जहां n नमूना आकार है। आप औपचारिक रूप से यह भी परीक्षण कर सकते हैं कि डर्बिन-वाटसन परीक्षण का उपयोग करके यह धारणा पूरी होती है या नहीं।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

इस धारणा का उल्लंघन कैसे किया जाता है इसके आधार पर, आपके पास कई विकल्प हैं:

• सकारात्मक क्रमिक सहसंबंध के लिए, मॉडल में आश्रित और/या स्वतंत्र चर के अंतराल जोड़ने पर विचार करें।
• नकारात्मक क्रमिक सहसंबंध के लिए, सुनिश्चित करें कि आपका कोई भी चर अति-विलंबित नहीं है।
• मौसमी सहसंबंध के लिए, मॉडल में मौसमी डमी जोड़ने पर विचार करें।

परिकल्पना 3: समरूपता

स्पष्टीकरण

रैखिक प्रतिगमन की अगली धारणा यह है कि x के प्रत्येक स्तर पर अवशेषों में निरंतर भिन्नता होती है। इसे होमोसेडैस्टिसिटी कहा जाता है। जब ऐसा नहीं होता है, तो अवशेष विषमलैंगिकता से पीड़ित होते हैं।

जब प्रतिगमन विश्लेषण में विषमलैंगिकता मौजूद होती है, तो विश्लेषण के परिणामों पर विश्वास करना मुश्किल हो जाता है। विशेष रूप से, विषमलैंगिकता प्रतिगमन गुणांक अनुमानों के विचरण को बढ़ाती है, लेकिन प्रतिगमन मॉडल इसका हिसाब नहीं देता है। इससे यह अधिक संभावना हो जाती है कि एक प्रतिगमन मॉडल यह दावा करेगा कि मॉडल में एक शब्द सांख्यिकीय रूप से महत्वपूर्ण है, जबकि वास्तव में ऐसा नहीं है।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

विषमलैंगिकता का पता लगाने का सबसे आसान तरीका एक फिटेड वैल्यू/अवशिष्ट प्लॉट बनाना है।

एक बार जब आप डेटा सेट में एक प्रतिगमन रेखा फिट कर लेते हैं, तो आप एक स्कैटरप्लॉट बना सकते हैं जो उन फिट किए गए मानों के अवशेषों के विरुद्ध मॉडल के फिट किए गए मान दिखाता है। नीचे दिया गया स्कैटरप्लॉट फिट किए गए मान बनाम अवशिष्ट का एक विशिष्ट प्लॉट दिखाता है जिसमें हेटेरोस्केडास्टिसिटी मौजूद है।

ध्यान दें कि जैसे-जैसे फिट किए गए मान बढ़ते हैं, अवशेष कैसे अधिक से अधिक फैलते हैं। यह “शंकु” आकार विषमलैंगिकता का एक उत्कृष्ट संकेत है:

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

विषमलैंगिकता को ठीक करने के तीन सामान्य तरीके हैं:

1. आश्रित चर को रूपांतरित करें। एक सामान्य परिवर्तन केवल आश्रित चर का लॉग लेना है। उदाहरण के लिए, यदि हम किसी शहर में फूल विक्रेताओं की संख्या (आश्रित चर) की भविष्यवाणी करने के लिए जनसंख्या आकार (स्वतंत्र चर) का उपयोग करते हैं, तो हम इसके बजाय किसी शहर में फूल विक्रेताओं की संख्या के लघुगणक की भविष्यवाणी करने के लिए जनसंख्या आकार का उपयोग करने का प्रयास कर सकते हैं। मूल आश्रित चर के बजाय आश्रित चर के लॉग का उपयोग करने से अक्सर विषमलैंगिकता गायब हो जाती है।

2. आश्रित चर को पुनः परिभाषित करें। आश्रित चर को फिर से परिभाषित करने का एक सामान्य तरीका कच्चे मूल्य के बजाय दर का उपयोग करना है। उदाहरण के लिए, किसी शहर में फूल विक्रेताओं की संख्या का अनुमान लगाने के लिए जनसंख्या आकार का उपयोग करने के बजाय, हम प्रति व्यक्ति फूल विक्रेताओं की संख्या का अनुमान लगाने के लिए जनसंख्या आकार का उपयोग कर सकते हैं। ज्यादातर मामलों में, यह बड़ी आबादी के भीतर स्वाभाविक रूप से होने वाली परिवर्तनशीलता को कम कर देता है क्योंकि हम फूल विक्रेताओं की संख्या के बजाय प्रति व्यक्ति फूल विक्रेताओं की संख्या को माप रहे हैं।

3. भारित प्रतिगमन का प्रयोग करें. विषमलैंगिकता को ठीक करने का दूसरा तरीका भारित प्रतिगमन का उपयोग करना है। इस प्रकार का प्रतिगमन प्रत्येक डेटा बिंदु को उसके फिट किए गए मान के भिन्नता के आधार पर एक भार प्रदान करता है। अनिवार्य रूप से, यह उन डेटा बिंदुओं को कम महत्व देता है जिनमें अधिक भिन्नताएं होती हैं, जिससे उनके अवशिष्ट वर्ग कम हो जाते हैं। जब उचित वजन का उपयोग किया जाता है, तो यह विषमलैंगिकता की समस्या को समाप्त कर सकता है।

परिकल्पना 4: सामान्यता

स्पष्टीकरण

रैखिक प्रतिगमन की अगली धारणा यह है कि अवशेष सामान्य रूप से वितरित होते हैं।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह जांचने के दो सामान्य तरीके हैं कि यह धारणा संतुष्ट है या नहीं:

1. QQ प्लॉट का उपयोग करके परिकल्पना को दृश्य रूप से सत्यापित करें ।

QQ प्लॉट, क्वांटाइल-क्वांटाइल प्लॉट के लिए संक्षिप्त, एक प्रकार का प्लॉट है जिसका उपयोग हम यह निर्धारित करने के लिए कर सकते हैं कि किसी मॉडल के अवशेष सामान्य वितरण का पालन करते हैं या नहीं। यदि प्लॉट पर बिंदु मोटे तौर पर एक सीधी विकर्ण रेखा बनाते हैं, तो सामान्यता की धारणा पूरी होती है।

निम्नलिखित QQ प्लॉट अवशेषों का एक उदाहरण दिखाता है जो मोटे तौर पर सामान्य वितरण का अनुसरण करता है:

हालाँकि, नीचे दिया गया QQ प्लॉट एक ऐसे मामले का उदाहरण दिखाता है जहां अवशेष स्पष्ट रूप से एक सीधी विकर्ण रेखा से विचलित होते हैं, जो दर्शाता है कि वे सामान्य वितरण का पालन नहीं करते हैं:

2. आप शापिरो-विल्क, कोलमोगोरोव-स्मिरोनोव, जार्के-बैरे या डी’ऑगोस्टिनो-पियर्सन जैसे औपचारिक सांख्यिकीय परीक्षणों का उपयोग करके भी सामान्यता धारणा की जांच कर सकते हैं। हालाँकि, ध्यान रखें कि ये परीक्षण बड़े नमूना आकारों के प्रति संवेदनशील होते हैं – यानी, वे अक्सर यह निष्कर्ष निकालते हैं कि जब आपका नमूना आकार बड़ा होता है तो अवशेष सामान्य नहीं होते हैं। यही कारण है कि इस परिकल्पना को सत्यापित करने के लिए QQ प्लॉट जैसी ग्राफिकल विधियों का उपयोग करना अक्सर आसान होता है।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि सामान्यता की धारणा पूरी नहीं होती है, तो आपके पास कई विकल्प हैं:

• सबसे पहले, जांचें कि आउटलेर्स का वितरण पर बड़ा प्रभाव न पड़े। यदि कोई आउटलेयर हैं, तो सुनिश्चित करें कि वे वास्तविक मान हैं और डेटा प्रविष्टि त्रुटियां नहीं हैं।
• फिर आप स्वतंत्र और/या आश्रित चर पर एक अरेखीय परिवर्तन लागू कर सकते हैं। सामान्य उदाहरणों में स्वतंत्र और/या आश्रित चर का लॉग, वर्गमूल, या व्युत्क्रम लेना शामिल है।

अग्रिम पठन:

सरल रेखीय प्रतिगमन का परिचय
प्रतिगमन विश्लेषण में विषमलैंगिकता को समझना
R में QQ प्लॉट कैसे बनाएं और उसकी व्याख्या कैसे करें