बेन्जामिनी-होचबर्ग प्रक्रिया के लिए एक गाइड

जब भी आप कोई सांख्यिकीय परीक्षण करते हैं, तो यह संभव है कि आपको शुद्ध संयोग से 0.05 से कम पी-वैल्यू मिलेगा, भले ही आपकी शून्य परिकल्पना सत्य हो।

उदाहरण के लिए, मान लें कि आप जानना चाहते हैं कि किसी पौधे की औसत ऊंचाई 10 इंच से अधिक है या नहीं। परीक्षण के लिए आपकी शून्य और वैकल्पिक परिकल्पनाएँ होंगी:

एच ₀ : μ = 10 इंच

एच _ए : μ > 10 इंच

इस परिकल्पना का परीक्षण करने के लिए, आप बाहर जा सकते हैं और मापने के लिए 20 पौधों का एक यादृच्छिक नमूना एकत्र कर सकते हैं। भले ही इस पौधे की प्रजाति की वास्तविक औसत ऊंचाई 10 इंच है, यह संभव है कि आपने 20 असामान्य रूप से लंबे पौधों का एक नमूना चुना है, जिससे आप शून्य परिकल्पना को अस्वीकार कर सकते हैं।

भले ही शून्य परिकल्पना सत्य थी (इस पौधे की औसत ऊँचाई वास्तव में 10 इंच थी), आपने इसे अस्वीकार कर दिया। आँकड़ों में, हम इसे “झूठी खोज” कहते हैं। आप एक खोज करने का दावा करते हैं – एक “महत्वपूर्ण परिणाम” – लेकिन यह वास्तव में गलत है।

अब एक साथ 100 सांख्यिकीय परीक्षण चलाने की कल्पना करें। 0.05 के अल्फा स्तर का उपयोग करते हुए, व्यक्तिगत परीक्षण के साथ झूठी खोज करने की केवल 5% संभावना है, लेकिन क्योंकि आप इतनी बड़ी संख्या में परीक्षण कर रहे हैं, आप उम्मीद करेंगे कि 100 में से केवल 5 ही झूठी खोजों का कारण बनेंगे।

आधुनिक दुनिया में, झूठी खोजें एक आम समस्या हो सकती हैं क्योंकि प्रौद्योगिकी ने शोधकर्ताओं को एक समय में सैकड़ों या हजारों सांख्यिकीय परीक्षण करने की अनुमति दी है।

उदाहरण के लिए, चिकित्सा शोधकर्ता एक समय में हजारों जीनों पर सांख्यिकीय परीक्षण कर सकते हैं। यहां तक कि केवल 5% की झूठी खोज दर के साथ, इसका मतलब है कि सैकड़ों परीक्षणों के परिणामस्वरूप झूठी खोजें हो सकती हैं।

झूठी खोज दर को नियंत्रित करने का एक तरीका बेन्जामिनी-होचबर्ग प्रक्रिया कहलाने वाली प्रक्रिया का उपयोग करना है।

बेन्जामिनी-होचबर्ग प्रक्रिया

बेन्जामिनी-होचबर्ग प्रक्रिया इस प्रकार काम करती है:

चरण 1: अपने सभी सांख्यिकीय परीक्षण करें और प्रत्येक परीक्षण के लिए पी-मान ज्ञात करें।

चरण 2: पी-मानों को अवरोही क्रम में रैंक करें, प्रत्येक को एक रैंक निर्दिष्ट करें: सबसे छोटे मान की रैंक 1 है, अगले सबसे छोटे मान की रैंक 2 है, आदि।

चरण 3: सूत्र (i/m)*Q का उपयोग करके, प्रत्येक पी-मान के लिए महत्वपूर्ण बेन्जामिनी-होचबर्ग मान की गणना करें

सोना:

i = पी मान की रैंक

एम = परीक्षणों की कुल संख्या

Q = आपकी चुनी गई झूठी खोज दर

चरण 4: क्रांतिक मान से कम सबसे बड़ा पी-मान ज्ञात करें। इस पी-वैल्यू से कम प्रत्येक पी-वैल्यू को महत्वपूर्ण के रूप में नामित करें।

निम्नलिखित उदाहरण दिखाता है कि इस प्रक्रिया को ठोस मूल्यों के साथ कैसे पूरा किया जाए।

उदाहरण

मान लीजिए कि शोधकर्ता यह निर्धारित करना चाहते हैं कि 20 अलग-अलग चर हृदय रोग से संबंधित हैं या नहीं। वे एक समय में 20 व्यक्तिगत सांख्यिकीय परीक्षण करते हैं और प्रत्येक परीक्षण के लिए एक पी-वैल्यू प्राप्त करते हैं। निम्न तालिका अवरोही क्रम में सूचीबद्ध प्रत्येक परीक्षण के लिए पी-मान दिखाती है।

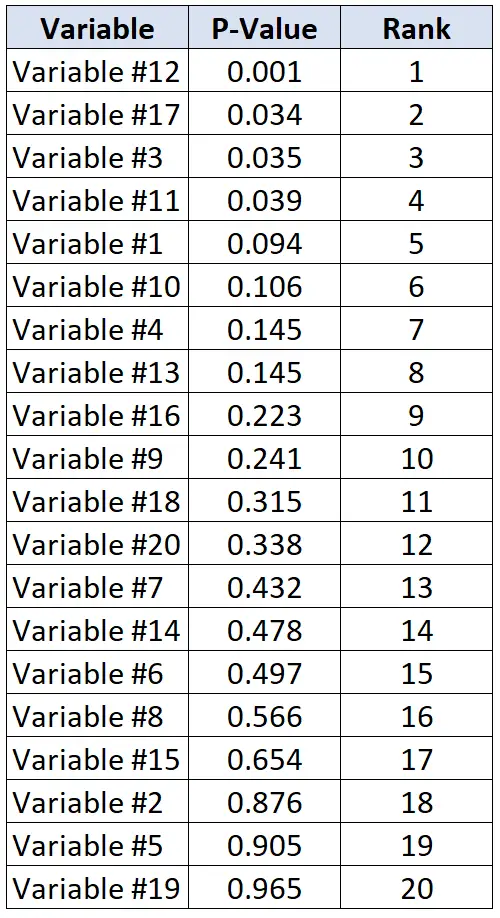
मान लीजिए कि शोधकर्ता 20% की झूठी खोज दर को स्वीकार करने को तैयार हैं। इसलिए, प्रत्येक पी-वैल्यू के लिए महत्वपूर्ण बेंजामिनी-होचबर्ग मान की गणना करने के लिए, हम निम्नलिखित सूत्र का उपयोग कर सकते हैं: (i/20)*0.2 जहां i = पी-वैल्यू की रैंक।

निम्न तालिका प्रत्येक व्यक्तिगत पी-मान के लिए महत्वपूर्ण बेन्जामिनी-होचबर्ग मान दिखाती है:

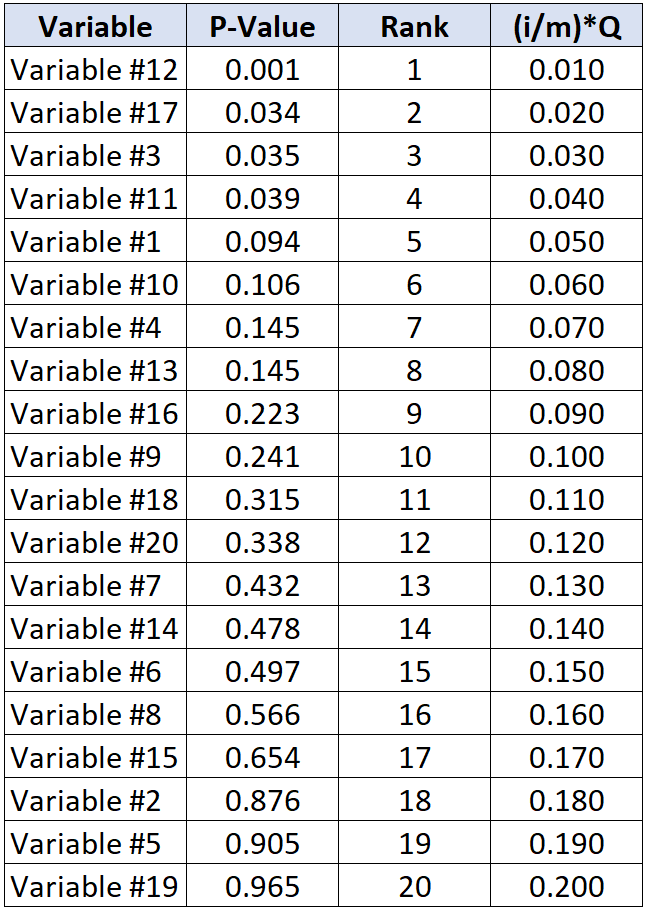
बेन्जामिनी-होचबर्ग महत्वपूर्ण मान के नीचे सबसे बड़े पी-मान वाला परीक्षण वेरिएबल #11 है, जिसका पी-मान 0.039 और बीएच महत्वपूर्ण मान 0.040 है।

इस प्रकार, यह परीक्षण और छोटे पी-वैल्यू वाले सभी परीक्षण महत्वपूर्ण माने जाएंगे।

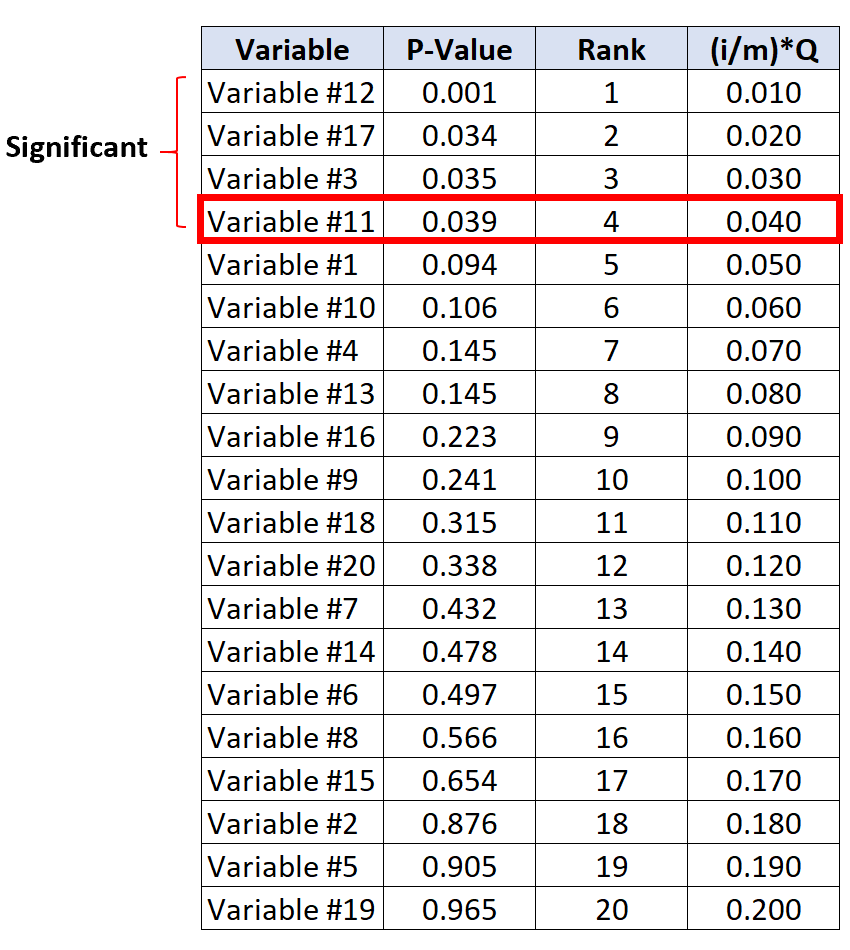
ध्यान दें कि भले ही वेरिएबल #17 और #3 का पी-वैल्यू उनके बीएच महत्वपूर्ण मानों से छोटा नहीं था, फिर भी उन्हें महत्वपूर्ण माना जाता है क्योंकि उनके पास वेरिएबल #11 की तुलना में छोटे पी-वैल्यू हैं।

झूठी खोज दर कैसे चुनें

बेन्जामिनी-होचबर्ग प्रक्रिया में सबसे महत्वपूर्ण चरणों में से एक झूठी खोज दर चुनना है। आपको डेटा एकत्र करने या सांख्यिकीय परीक्षण करने से पहले अपनी झूठी खोज दर चुननी चाहिए।

आमतौर पर, आप अपने विश्लेषण के खोजपूर्ण चरण के दौरान बड़ी संख्या में सांख्यिकीय परीक्षण करेंगे, जिसके बाद आप अपने परिणामों का और पता लगाने के लिए अन्य परीक्षण करेंगे।

यदि अनुवर्ती परीक्षण सस्ता है, तो आप उच्चतर झूठी खोज दर निर्धारित करने पर विचार कर सकते हैं, क्योंकि भले ही आपके पास कुछ झूठी खोजें हों, आपको बाद के परीक्षण में उन झूठी खोजों का पता चलने की संभावना है।

इसके अतिरिक्त, यदि किसी महत्वपूर्ण खोज को चूकने की लागत अधिक है, तो आप अपनी झूठी खोज दर को बढ़ाना चाह सकते हैं ताकि आप कुछ भी महत्वपूर्ण न चूकें।

आपके शोध की लागत और किसी भी महत्वपूर्ण निष्कर्ष को न चूकने के महत्व के आधार पर, झूठी खोज की दर स्थिति-दर-स्थिति अलग-अलग होगी।

अतिरिक्त संसाधन

पी मूल्यों और सांख्यिकीय महत्व की व्याख्या
प्रति परिवार त्रुटि दर क्या है?