अंतरचतुर्थक सीमा (या अंतरचतुर्थक सीमा)

यह आलेख बताता है कि अंतरचतुर्थक सीमा, जिसे अंतरचतुर्थक श्रेणी भी कहा जाता है, क्या है। आप एक ठोस उदाहरण के साथ यह भी देख पाएंगे कि अंतरचतुर्थक सीमा की गणना कैसे की जाती है। आप सीखेंगे कि अंतरचतुर्थक सीमा क्या है और अंतराल के साथ क्या अंतर है। इसके अतिरिक्त, आप ऑनलाइन कैलकुलेटर से किसी भी डेटा सेट की अंतरचतुर्थक सीमा की गणना कर सकते हैं।

अंतरचतुर्थक (या अंतःचतुर्थक) सीमा क्या है?

अंतरचतुर्थक श्रेणी, जिसे अंतरचतुर्थक श्रेणी भी कहा जाता है, सांख्यिकीय फैलाव का एक माप है जो तीसरे और पहले चतुर्थक के बीच अंतर को इंगित करता है। इसलिए, सांख्यिकीय डेटा सेट की अंतरचतुर्थक सीमा की गणना करने के लिए, आपको पहले तीसरा और पहला चतुर्थक ढूंढना होगा और फिर उन्हें घटाना होगा।

संक्षेप में, अंतरचतुर्थक सीमा को संक्षिप्त नाम IQR द्वारा व्यक्त किया जाता है।

इंटरक्वेर्टाइल रेंज की सबसे लाभप्रद विशेषताओं में से एक यह है कि यह एक मजबूत आँकड़ा है, अर्थात इसमें आउटलेर्स के लिए उच्च मजबूती है। चूंकि इंटरक्वेर्टाइल रेंज की गणना में चरम मूल्यों को ध्यान में नहीं रखा जाता है, इसलिए नए आउटलेर्स दिखाई देने पर इसका मूल्य बहुत कम भिन्न होगा।

स्पष्ट रूप से अंतरचतुर्थक सीमा के अलावा फैलाव के अन्य उपाय भी हैं, सबसे अच्छी ज्ञात मीट्रिक सीमा, विचरण, मानक (या मानक) विचलन, माध्य विचलन और भिन्नता का गुणांक हैं।

अंतरचतुर्थक (या अंतरचतुर्थक) श्रेणी की गणना कैसे करें

आंकड़ों में, किसी डेटा सेट की अंतरचतुर्थक सीमा (या अंतरचतुर्थक श्रेणी) की गणना करने के लिए, आपको पहले डेटा सेट के पहले और तीसरे चतुर्थक को ढूंढना होगा, फिर पहले चतुर्थक को घटाकर तीसरे चतुर्थक के घटाव की गणना करनी होगी।

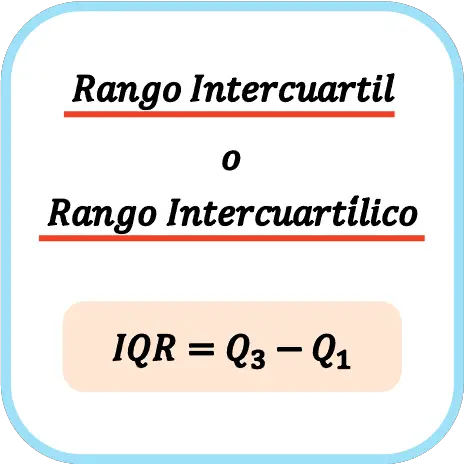
इसलिए, अंतरचतुर्थक सीमा या अंतरचतुर्थक सीमा की गणना करने का सूत्र है:

👉 आप किसी भी डेटा सेट के लिए इंटरक्वेर्टाइल रेंज की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

इसलिए, यह आवश्यक है कि आप जानें कि सांख्यिकीय नमूने के चतुर्थक की गणना कैसे की जाती है। यही कारण है कि मेरा सुझाव है कि आप आगे बढ़ने से पहले निम्नलिखित लेख देखें और फिर स्पष्टीकरण जारी रखें।

अंतरचतुर्थक (या अंतरचतुर्थक) श्रेणी का उदाहरण

अंतरचतुर्थक श्रेणी (या अंतरचतुर्थक श्रेणी) की परिभाषा और सूत्र को देखते हुए, नीचे एक हल किया गया अभ्यास दिया गया है ताकि आप देख सकें कि इस प्रकार के फैलाव माप की गणना कैसे की जाती है।

• हम सांख्यिकीय रूप से विश्लेषण करना चाहते हैं कि क्या किसी कंपनी में निवेश करना एक अच्छा विचार है। ऐसा करने के लिए, हमने पिछले 15 महीनों में इस कंपनी के स्टॉक मूल्य पर डेटा एकत्र किया। निम्नलिखित तालिका में आप देखे गए डेटा को निम्नतम से उच्चतम क्रम में देख सकते हैं। इस डेटा सेट के लिए अंतरचतुर्थक सीमा की गणना करें।

जैसा कि हमने पिछले अनुभाग में देखा, नमूने की अंतरचतुर्थक सीमा (या अंतरचतुर्थक श्रेणी) प्राप्त करने के लिए, हमें पहले पहले और तीसरे चतुर्थक की गणना करनी होगी।

पहला चतुर्थक मानों के पहले आधे भाग का माध्यिका है, जो €8.95/शेयर से मेल खाता है।

दूसरी ओर, तीसरा चतुर्थक मूल्यों के दूसरे भाग का मध्यवर्ती मूल्य है, इसलिए यह €9.83/शेयर है।

अत: अंतरचतुर्थक श्रेणी ज्ञात करने के लिए, बस सूत्र लागू करें और प्रथम चतुर्थक को घटाकर तीसरे चतुर्थक को घटा दें।

इंटरक्वेर्टाइल (या इंटरक्वेर्टाइल) रेंज कैलकुलेटर

इसकी अंतःचतुर्थक सीमा या अंतःचतुर्थक सीमा की गणना करने के लिए निम्नलिखित कैलकुलेटर में एक सांख्यिकीय डेटा सेट दर्ज करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

इंटरक्वेर्टाइल रेंज और रेंज के बीच अंतर

आँकड़ों में, अंतरचतुर्थक सीमा (या अंतरचतुर्थक श्रेणी) और अंतराल के बीच का अंतर वे मान हैं जो गणना करने के लिए लिए जाते हैं। अंतरचतुर्थक सीमा तीसरे और पहले चतुर्थक के बीच का अंतर है, जबकि सीमा नमूने के चरम मूल्यों के बीच का अंतर है।

इस प्रकार, इंटरक्वेर्टाइल रेंज केंद्रीय डेटा का उपयोग करके नमूने के फैलाव को मापती है, जबकि अंतराल चरम डेटा का उपयोग करके नमूने के फैलाव को मापता है।

इसलिए, सांख्यिकीय सीमा आउटलेर्स से बहुत अधिक प्रभावित होती है क्योंकि वे आमतौर पर डेटा सेट के न्यूनतम या अधिकतम का प्रतिनिधित्व करते हैं। इस प्रकार, अंतराल पर अंतरचतुर्थक सीमा का एक लाभ यह है कि इसमें अधिक मजबूती है।

अंतरचतुर्थक (या अंतरचतुर्थक) श्रेणी का उपयोग किसके लिए किया जाता है?

मुख्य रूप से, डेटा सेट के वितरण को मापने के लिए इंटरक्वेर्टाइल रेंज (या इंटरक्वेर्टाइल रेंज) का उपयोग किया जाता है। हालांकि किसी नमूने के फैलाव का विश्लेषण करने के लिए अधिक सांख्यिकीय उपायों की गणना की आवश्यकता होती है, इंटरक्वेर्टाइल रेंज यह अंदाजा देती है कि नमूना कितना फैला हुआ है, कम से कम केंद्रीय मान।

इसलिए अंतरचतुर्थक श्रेणी की व्याख्या अपेक्षाकृत सरल है। अंतरचतुर्थक श्रेणी का मान जितना अधिक होगा, नमूने में मध्य डेटा उतना ही अधिक बिखरा हुआ होगा, और अंतरचतुर्थक सीमा जितनी छोटी होगी, मध्य डेटा उतना ही करीब होगा।

इसके अतिरिक्त, इंटरक्वेर्टाइल रेंज बॉक्स-एंड-व्हिस्कर प्लॉट बनाने के लिए भी उपयोगी है, जो शेयर बाजार पर स्टॉक मूल्य व्यवहार का विश्लेषण करने के लिए व्यापक रूप से उपयोग किया जाने वाला आरेख है।