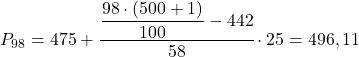प्रतिशत (सांख्यिकी)

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि प्रतिशतक क्या है और इसकी गणना कैसे की जाती है। आपको हल किए गए प्रतिशतक अभ्यास मिलेंगे और इसके अलावा, आप ऑनलाइन कैलकुलेटर के साथ अपने डेटा नमूने के किसी भी प्रतिशतक की गणना करने में सक्षम होंगे।

प्रतिशतक क्या हैं?

आंकड़ों में, प्रतिशतक वे मान हैं जो ऑर्डर किए गए डेटा के एक सेट को एक सौ बराबर भागों में विभाजित करते हैं। तो, एक प्रतिशतक उस मान को इंगित करता है जिसके नीचे डेटा सेट का एक प्रतिशत गिरता है।

उदाहरण के लिए, 35वां प्रतिशतक मान प्रेक्षित डेटा के 35% से अधिक है, लेकिन बाकी डेटा से कम है।

प्रतिशतक को बड़े अक्षर P और प्रतिशतक सूचकांक द्वारा दर्शाया जाता है, अर्थात, पहला प्रतिशतक P ₁ है, 40वाँ प्रतिशतक P ₄₀ है, 79वाँ प्रतिशतक P ₇₉ है, इत्यादि।

👉 आप किसी भी डेटा सेट के प्रतिशत की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

इसी प्रकार, प्रतिशतक चतुर्थक, क्विंटाइल और डेसील के साथ-साथ गैर-केंद्रीय स्थिति का एक माप है। आप हमारी वेबसाइट पर इनमें से प्रत्येक मात्रा प्रकार का अर्थ देख सकते हैं।

यह ध्यान दिया जाना चाहिए कि प्रतिशत शब्द का उपयोग किसी बच्चे के वजन और ऊंचाई की तुलना अन्य शिशुओं के मानक मूल्यों के साथ करने के लिए भी किया जाता है, क्योंकि रिकॉर्ड किए गए मूल्यों के साथ विकास तालिकाएं हैं जो यह निर्धारित करने में मदद करती हैं कि बच्चा सही ढंग से बढ़ रहा है या नहीं। . .

प्रतिशत की गणना कैसे करें

किसी सांख्यिकीय डेटा श्रृंखला के प्रतिशतक की स्थिति की गणना करने के लिए, आपको प्रतिशतक संख्या को डेटा बिंदुओं की कुल संख्या के योग से एक को गुणा करना होगा और परिणाम को एक सौ से विभाजित करना होगा।

इसलिए प्रतिशतक सूत्र है:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

कृपया ध्यान दें: यह सूत्र हमें प्रतिशतक की स्थिति बताता है, लेकिन उसका मान नहीं। प्रतिशतक सूत्र द्वारा प्राप्त स्थिति पर स्थित डेटा होगा।

हालाँकि, कभी-कभी इस सूत्र का परिणाम हमें दशमलव संख्या देगा, इसलिए हमें दो मामलों में अंतर करना होगा, यह इस बात पर निर्भर करेगा कि परिणाम दशमलव संख्या है या नहीं:

यदि सूत्र का परिणाम दशमलव भाग के बिना एक संख्या है, तो प्रतिशतक उस डेटा से मेल खाता है जो उपरोक्त सूत्र द्वारा प्रदान की गई स्थिति में है।
यदि सूत्र परिणाम दशमलव भाग वाली एक संख्या है, तो सटीक प्रतिशत मान की गणना निम्न सूत्र का उपयोग करके की जाती है:

$P=x_i+d\cdot (x_{i+1}-x_i)$

जहाँ x _i और x _i+1 उन स्थितियों की संख्याएँ हैं जिनके बीच पहले सूत्र द्वारा प्राप्त संख्या स्थित है, और d पहले सूत्र द्वारा प्राप्त संख्या का दशमलव भाग है।

अब आप सोच सकते हैं कि किसी सांख्यिकीय नमूने या जनसंख्या का प्रतिशत ज्ञात करना जटिल है क्योंकि विधि में कई चरण शामिल हैं, लेकिन यह वास्तव में आसान है। निम्नलिखित दो ठोस उदाहरण पढ़ें और मुझे यकीन है कि आप इसे बेहतर ढंग से समझेंगे।

ध्यान दें : प्रतिशतक की गणना कैसे करें, इस पर वैज्ञानिक समुदाय अभी तक पूरी तरह से सहमत नहीं है, इसलिए आप एक सांख्यिकी पुस्तक पा सकते हैं जो इसे थोड़ा अलग तरीके से समझाती है।

प्रतिशत गणना उदाहरण

जैसा कि आपने ऊपर किसी नमूने के प्रतिशतक ज्ञात करने के स्पष्टीकरण में देखा, गणना इस पर निर्भर करती है कि पहले सूत्र का परिणाम दशमलव है या नहीं। इसीलिए नीचे आपको दो हल किए गए उदाहरण मिलेंगे, प्रत्येक मामले के लिए एक।

उदाहरण 1

निम्नलिखित तालिका में दिखाए गए डेटा से, 1, 43वें और 89वें प्रतिशतक की गणना करें।

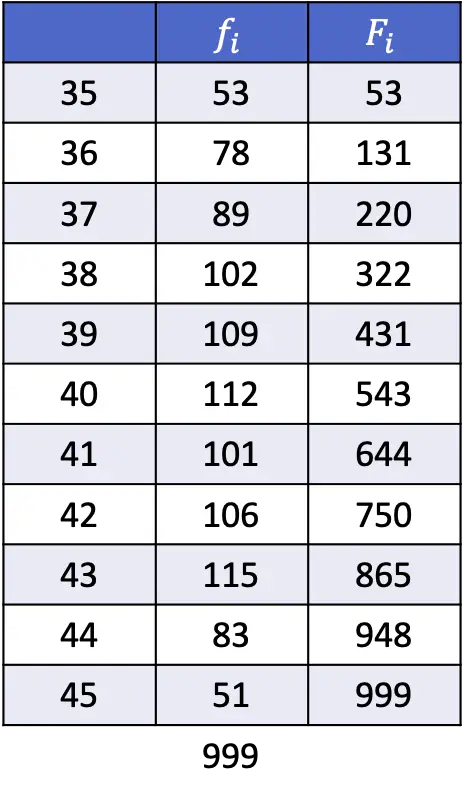
जैसा कि पिछले अनुभाग में बताया गया है, प्रतिशतक की स्थिति ज्ञात करने का सूत्र है:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

इस मामले में, इस अभ्यास के लिए नमूना आकार 999 सांख्यिकीय डेटा है, इसलिए पहले प्रतिशतक की स्थिति की गणना करने के लिए हमें n के लिए 999 और k के लिए 1 को प्रतिस्थापित करना होगा:

$\cfrac{1\cdot (999+1)}{100}=10\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_1=35$

तो पहला प्रतिशतक वह होगा जिसकी संचयी निरपेक्ष आवृत्ति तुरंत 10 से अधिक है, जो इस मामले में 35 है क्योंकि इसकी संचयी निरपेक्ष आवृत्ति 53 है।

43वाँ प्रतिशतक निर्धारित करने के लिए आपको उसी सूत्र का उपयोग करना होगा लेकिन, जाहिर है, इस बार हम k को 43 से बदल देंगे।

$\cfrac{43\cdot (999+1)}{100}=430\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{43}=39$

430 से ठीक ऊपर की पूर्ण संचयी आवृत्ति डेटा 39 का 431 है, इसलिए 43वां प्रतिशतक 39 के बराबर है।

अंत में, हम 89वाँ प्रतिशतक प्राप्त करने के लिए वही सूत्र लागू करते हैं:

$\cfrac{89\cdot (999+1)}{100}=890\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{89}=44$

मान 44 की संचयी निरपेक्ष आवृत्ति 948 है, जो 890 से तुरंत अधिक है। इसलिए, 89वाँ प्रतिशतक 44 है।

उदाहरण 2

निम्नलिखित डेटा श्रृंखला के 35वें और 67वें प्रतिशतक ज्ञात कीजिए:

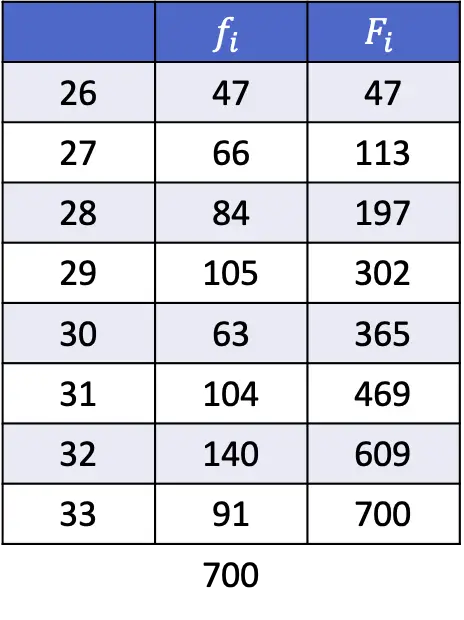
भले ही इस अभ्यास में हमें अधिक गणनाएँ करनी पड़े, सिद्धांत अभी भी वही है: हमें निम्नलिखित अभिव्यक्ति के साथ प्रतिशतक स्थिति की गणना करनी चाहिए।

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,\ldots ,97,98,99$

इस प्रकार, 35वें प्रतिशतक की गणना करने के लिए हम k को 35 से और n को डेटा की कुल संख्या, यानी 700 से प्रतिस्थापित करते हैं:

$\cfrac{35\cdot (700+1)}{100}=245,35$

लेकिन इस बार हमें सूत्र से एक दशमलव संख्या मिली, इसलिए हमें सटीक प्रतिशत मान की गणना करने के लिए निम्नलिखित बीजगणितीय अभिव्यक्ति को लागू करने की आवश्यकता है:

$P=x_i+d\cdot (x_{i+1}-x_i)$

पहले सूत्र द्वारा दी गई संख्या 245.35 है, इसलिए 35वां प्रतिशतक स्थिति 245 और 246 के बीच है, जो क्रमशः 29 और 29 मानों से मेल खाता है। इसलिए, x _i 29 है, x _i+1 29 है और d प्राप्त संख्या के दशमलव भाग के बराबर है, यानी 0.35।

$P_{35}=29+0,35\cdot (29-29)=29$

67वाँ प्रतिशतक ज्ञात करने के लिए, हमें उसी विधि का उपयोग करने की आवश्यकता है। हम पहले प्रतिशतक स्थिति की गणना करते हैं:

$\cfrac{67\cdot (700+1)}{100}=469,67$

परिणामी संख्या 469.67 इंगित करती है कि प्रतिशतक स्थिति 469 और 470 के बीच होगा, जिसका मान 31 और 32 है। इसलिए, हम सटीक प्रतिशतक मान ज्ञात करने के लिए प्रक्रिया में दूसरे सूत्र का उपयोग करते हैं:

$P_{67}=31+0,67\cdot (32-31)=31,67$

प्रतिशतक कैलकुलेटर

निम्नलिखित कैलकुलेटर में एक सांख्यिकीय डेटा सेट और वह प्रतिशत संख्या दर्ज करें जिसकी आप गणना करना चाहते हैं। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

समूहीकृत डेटा में प्रतिशतक

जब डेटा को समूहों में वर्गीकृत किया जाता है तो प्रतिशतक की गणना करने के लिए, हमें सबसे पहले निम्नलिखित सूत्र का उपयोग करके उस समूह या वर्ग को ढूंढना होगा जिसमें प्रतिशतक आता है:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

इसलिए प्रतिशतक उस अंतराल में होगा जिसकी पूर्ण आवृत्ति पिछली अभिव्यक्ति में प्राप्त संख्या से तुरंत अधिक है।

और एक बार जब हम पहले से ही उस अंतराल को जान लेते हैं जिससे प्रतिशतक संबंधित है, तो हमें प्रतिशतक का सटीक मान ज्ञात करने के लिए निम्नलिखित सूत्र को लागू करना होगा:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,\ldots ,97,98,99$

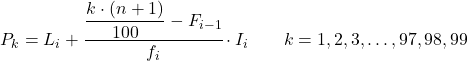
सोना:

L _i उस अंतराल की निचली सीमा है जिसमें प्रतिशतक निहित है।
n प्रेक्षणों की कुल संख्या है।
F _i-1 पिछले अंतराल की संचयी निरपेक्ष आवृत्ति है।
f _i उस अंतराल की पूर्ण आवृत्ति है जिसमें प्रतिशतक निहित है।
I _i शतमक अंतराल की चौड़ाई है।

जब डेटा अंतरालों में व्यक्त किया जाता है तो प्रतिशतक कैसे प्राप्त करें, इस पर चरण-दर-चरण अभ्यास नीचे दिया गया है। विशेष रूप से, 29वें, 52वें और 98वें प्रतिशतक की गणना की जाती है।

इस नमूने में डेटा को अंतराल के रूप में समूहीकृत किया गया है, इसलिए हमें प्रतिशतक निर्धारित करने के लिए दो चरण करने की आवश्यकता है: पहले हमें उस अंतराल को ढूंढना होगा जिसमें प्रतिशतक आता है, फिर प्रतिशतक के सटीक मान की गणना करने के लिए सूत्र लागू करें। शतमक.

इस प्रकार, हम निम्नलिखित अभिव्यक्ति के साथ 29वें प्रतिशतक की स्थिति पाते हैं:

$\cfrac{k\cdot (n+1)}{100}$

$\cfrac{29\cdot (500+1)}{100} =145,29 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [350,375)$

प्रतिशतक अंतराल वह होगा जिसकी संचयी निरपेक्ष आवृत्ति तुरंत 145.29 से अधिक है, जो इस मामले में अंतराल [350.375) है जिसकी संचयी निरपेक्ष आवृत्ति 175 है। और एक बार जब हम प्रतिशतक अंतराल जान लेते हैं, तो हम इसकी गणना करने के लिए निम्नलिखित सूत्र लागू करते हैं सही मूल्य:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i$

$P_{29}=350+\cfrac{\displaystyle\frac{29\cdot (500+1)}{100}-131}{44}\cdot 25=358,12$

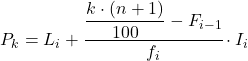
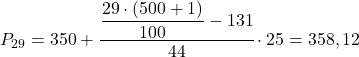
अब हम 52वें प्रतिशतक की गणना के लिए वही प्रक्रिया दोहराते हैं। हम पहले इसके अंतराल की गणना करते हैं:

$\cfrac{52\cdot (500+1)}{100} =260,52 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [400,425)$

52वाँ प्रतिशतक अंतराल [400.425) है क्योंकि इसकी संचयी निरपेक्ष आवृत्ति (298) 260.52 से ठीक ऊपर है। इसलिए प्रतिशतक का सटीक मान होगा:

$P_{52}=400+\cfrac{\displaystyle\frac{52\cdot (500+1)}{100}-234}{64}\cdot 25=410,36$

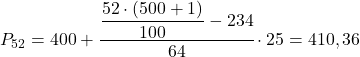
अंत में, हम 98वाँ प्रतिशतक ज्ञात करेंगे। हमेशा की तरह, हम पहले उस अंतराल की गणना करते हैं जहां यह स्थित है:

$\cfrac{98\cdot (500+1)}{100} =490,98 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [475,500)$

और एक बार जब हम उस अंतराल को जान लेते हैं जहां प्रतिशतक स्थित है, तो हम निम्नलिखित सूत्र के साथ इसके सटीक मूल्य की गणना करते हैं:

$P_{98}=475+\cfrac{\displaystyle\frac{98\cdot (500+1)}{100}-442}{58}\cdot 25=496,11$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

प्रतिशतक क्या हैं?

प्रतिशत की गणना कैसे करें

प्रतिशत गणना उदाहरण

उदाहरण 1

उदाहरण 2

प्रतिशतक कैलकुलेटर

समूहीकृत डेटा में प्रतिशतक

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने