मध्यम अंतर

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि माध्य विचलन क्या है और इसकी गणना कैसे की जाती है। आपको औसत विचलन की गणना के ठोस उदाहरण भी मिलेंगे। और, इसके अलावा, आप ऑनलाइन कैलकुलेटर का उपयोग करके किसी भी सांख्यिकीय डेटा सेट के औसत विचलन की गणना करने में सक्षम होंगे।

माध्य विचलन क्या है?

माध्य विचलन , जिसे माध्य निरपेक्ष विचलन भी कहा जाता है, सांख्यिकीय फैलाव का एक माप है।

डेटा सेट का माध्य विचलन पूर्ण विचलन का औसत है । इसलिए, औसत विचलन अंकगणित माध्य से प्रत्येक डेटा आइटम के विचलन के योग को डेटा आइटम की कुल संख्या से विभाजित करने के बराबर है।

दूसरे शब्दों में, औसत विचलन का सूत्र इस प्रकार है:

👉 आप किसी भी डेटा सेट के औसत विचलन की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

सांख्यिकी में माध्य विचलन को माध्य निरपेक्ष विचलन भी कहा जाता है।

औसत विचलन की व्याख्या इस प्रकार की जाती है: औसत विचलन का मूल्य जितना अधिक होगा, इसका मतलब है कि डेटा, औसतन, अंकगणितीय माध्य से आगे है; इसके विपरीत, औसत विचलन जितना कम होगा, मूल्य उतना ही करीब होगा। डेटा है. इसलिए औसत विचलन डेटा श्रृंखला के फैलाव को इंगित करता है।

वितरित माने जाने वाले अन्य माप हैं सीमा, अंतरचतुर्थक सीमा, मानक विचलन (या मानक विचलन), विचरण और भिन्नता का गुणांक।

औसत विचलन की गणना कैसे करें

किसी डेटा श्रृंखला के औसत विचलन की गणना करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

सांख्यिकीय डेटा सेट के अंकगणितीय माध्य की गणना करें ।
माध्य से प्रत्येक डेटा बिंदु के विचलन की गणना करें, जिसे डेटा और माध्य के बीच अंतर के निरपेक्ष मान के रूप में परिभाषित किया गया है।
पिछले चरण में गणना किए गए सभी अंतरों को जोड़ें।
डेटा की कुल संख्या से विभाजित करें. प्राप्त परिणाम डेटा श्रृंखला का औसत विचलन है।

संक्षेप में, औसत विचलन ज्ञात करने के लिए जिस सूत्र को लागू किया जाना चाहिए वह है:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

औसत विचलन की गणना का उदाहरण

माध्य विचलन की परिभाषा पर विचार करते हुए, सांख्यिकीय नमूने के माध्य विचलन की गणना का चरण-दर-चरण हल किया गया उदाहरण नीचे दिया गया है। इस तरह आप बेहतर ढंग से समझ पाएंगे कि औसत विचलन कैसे प्राप्त करें।

एक विश्लेषक पिछले वर्ष में किसी कंपनी के आर्थिक परिणामों का अध्ययन करता है और उसके पास उक्त वर्ष की प्रत्येक तिमाही के दौरान कंपनी द्वारा प्राप्त लाभ की जानकारी होती है: 2, 3, 7 और 5 मिलियन डॉलर। डेटा का औसत विचलन क्या है?

सबसे पहले, हमें डेटा को औसत करने की आवश्यकता है, इसलिए हम अवलोकनों की कुल संख्या (4) से योग और भाग देते हैं:

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

एक बार जब हम अंकगणितीय माध्य की गणना कर लेते हैं, तो हम माध्य विचलन सूत्र का उपयोग करते हैं:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

हम डेटा को सूत्र में प्रतिस्थापित करते हैं:

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

हम अंश में गणना करते हैं:

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

और अंत में, हम नमूने का औसत विचलन प्राप्त करने के लिए डेटा की कुल संख्या से विभाजित करते हैं:

$D_{\overline{x}}=1,75$

औसत विचलन कैलक्यूलेटर

इसके औसत विचलन की गणना करने के लिए निम्नलिखित कैलकुलेटर में सांख्यिकीय डेटा का एक सेट दर्ज करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

समूहीकृत डेटा के लिए औसत विचलन

अंतरालों में समूहीकृत डेटा के माध्य विचलन की गणना करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

सांख्यिकीय डेटा सेट का अंकगणितीय माध्य निर्धारित करें। चूँकि डेटा को समूहीकृत किया गया है, औसत की गणना करने के लिए अभिव्यक्ति है:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

माध्य से प्रत्येक अंतराल के विचलन की गणना करें, जो वर्ग ग्रेड और माध्य के बीच अंतर के पूर्ण मूल्य के बराबर है।

$|x_i-\overline{x}|$

प्रत्येक अंतराल के विचलन को उसकी पूर्ण आवृत्ति से गुणा करें।

$|x_i-\overline{x}|\cdot f_i$

पिछले चरण के सभी परिणाम जोड़ें, फिर डेटा की कुल संख्या से विभाजित करें। प्राप्त परिणाम अंतरालों में समूहीकृत नमूने का औसत विचलन है।

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

अंत में, समूहीकृत डेटा से औसत विचलन प्राप्त करने का सूत्र है:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

जब डेटा को समूहीकृत किया जाता है, तो इसका आमतौर पर मतलब होता है कि बहुत सारा डेटा है और औसत विचलन खोजने में कई चरण शामिल होते हैं। इसलिए, गणना करने के लिए आमतौर पर आवृत्ति तालिकाओं का उपयोग किया जाता है।

जब डेटा को अंतरालों में समूहीकृत किया जाता है तो माध्य विचलन की गणना कैसे करें, इस पर चरण-दर-चरण अभ्यास नीचे दिया गया है:

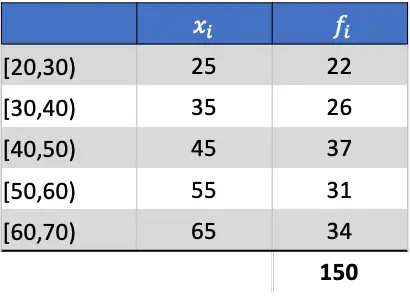
करने वाली पहली चीज़ समूहीकृत डेटा के औसत की गणना करना है। ऐसा करने के लिए, हम क्लास नोट को उसकी आवृत्ति से गुणा करके तालिका में एक कॉलम जोड़ते हैं:

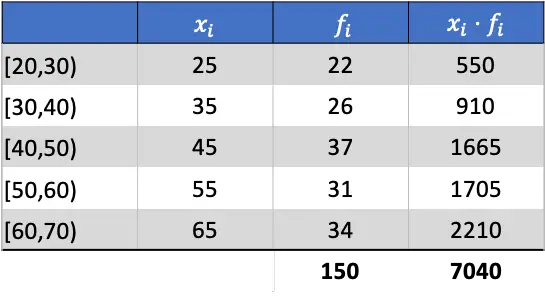
इसलिए अंकगणितीय माध्य जोड़े गए कॉलम के योग को पूर्ण आवृत्तियों के योग से विभाजित करने का परिणाम होगा:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

अब जब हमें डेटा का माध्य पता है, तो हम माध्य विचलन ज्ञात करने के लिए सभी आवश्यक कॉलम जोड़ सकते हैं:

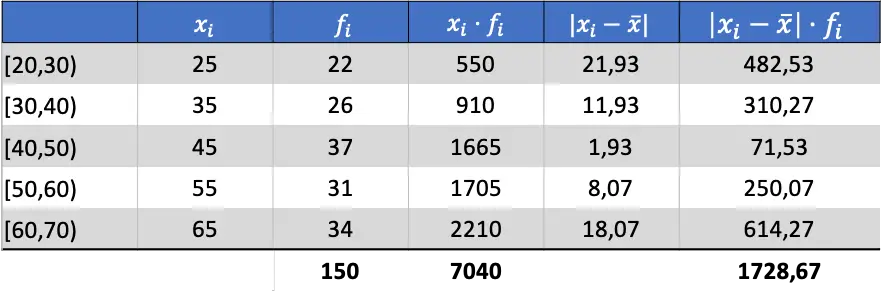
इस प्रकार, औसत विचलन प्राप्त करने के लिए आपको अंतिम कॉलम के योग को अवलोकनों की कुल संख्या से विभाजित करना होगा:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने