आर में द्विघात प्रतिगमन कैसे करें

जब दो चरों में एक रैखिक संबंध होता है, तो हम अक्सर उनके संबंध को मापने के लिए सरल रैखिक प्रतिगमन का उपयोग कर सकते हैं।

हालाँकि, जब दो चरों में द्विघात संबंध होता है, तो हम उनके संबंध को मापने के लिए द्विघात प्रतिगमन का उपयोग कर सकते हैं।

यह ट्यूटोरियल बताता है कि आर में द्विघात प्रतिगमन कैसे करें।

उदाहरण: आर में द्विघात प्रतिगमन

मान लीजिए हम काम किए गए घंटों की संख्या और रिपोर्ट की गई खुशी के बीच संबंध को समझना चाहते हैं। हमारे पास 11 अलग-अलग लोगों के लिए प्रति सप्ताह काम किए गए घंटों की संख्या और खुशी के रिपोर्ट किए गए स्तर (0 से 100 के पैमाने पर) पर निम्नलिखित डेटा है:

R में द्विघात प्रतिगमन मॉडल को फिट करने के लिए निम्नलिखित चरणों का उपयोग करें।

चरण 1: डेटा दर्ज करें.

सबसे पहले, हम एक डेटा फ़्रेम बनाएंगे जिसमें हमारा डेटा होगा:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

चरण 2: डेटा को विज़ुअलाइज़ करें।

इसके बाद, हम डेटा की कल्पना करने के लिए एक सरल स्कैटरप्लॉट बनाएंगे।

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

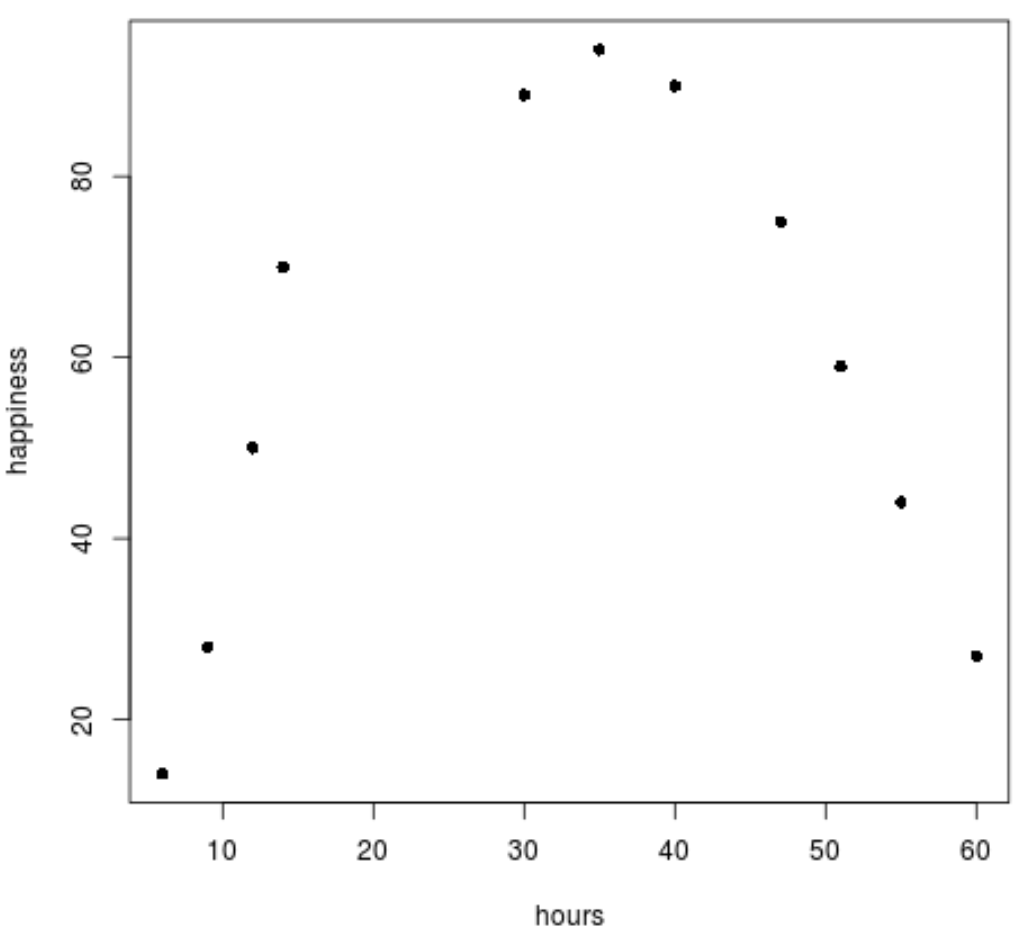
हम स्पष्ट रूप से देख सकते हैं कि डेटा एक रैखिक पैटर्न का पालन नहीं करता है।

चरण 3: एक सरल रैखिक प्रतिगमन मॉडल फिट करें।

इसके बाद, हम यह देखने के लिए एक सरल रैखिक प्रतिगमन मॉडल फिट करेंगे कि यह डेटा में कितनी अच्छी तरह फिट बैठता है:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

मॉडल द्वारा बताई गई खुशी में कुल भिन्नता केवल 4.46% है, जैसा कि एकाधिक आर-वर्ग मान द्वारा दिखाया गया है।

चरण 4: एक द्विघात प्रतिगमन मॉडल फिट करें।

इसके बाद, हम एक द्विघात प्रतिगमन मॉडल फिट करेंगे।

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

मॉडल द्वारा बताई गई खुशी में कुल अंतर बढ़कर 96.02% हो गया।

हम यह देखने के लिए निम्नलिखित कोड का उपयोग कर सकते हैं कि मॉडल डेटा में कितनी अच्छी तरह फिट बैठता है:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

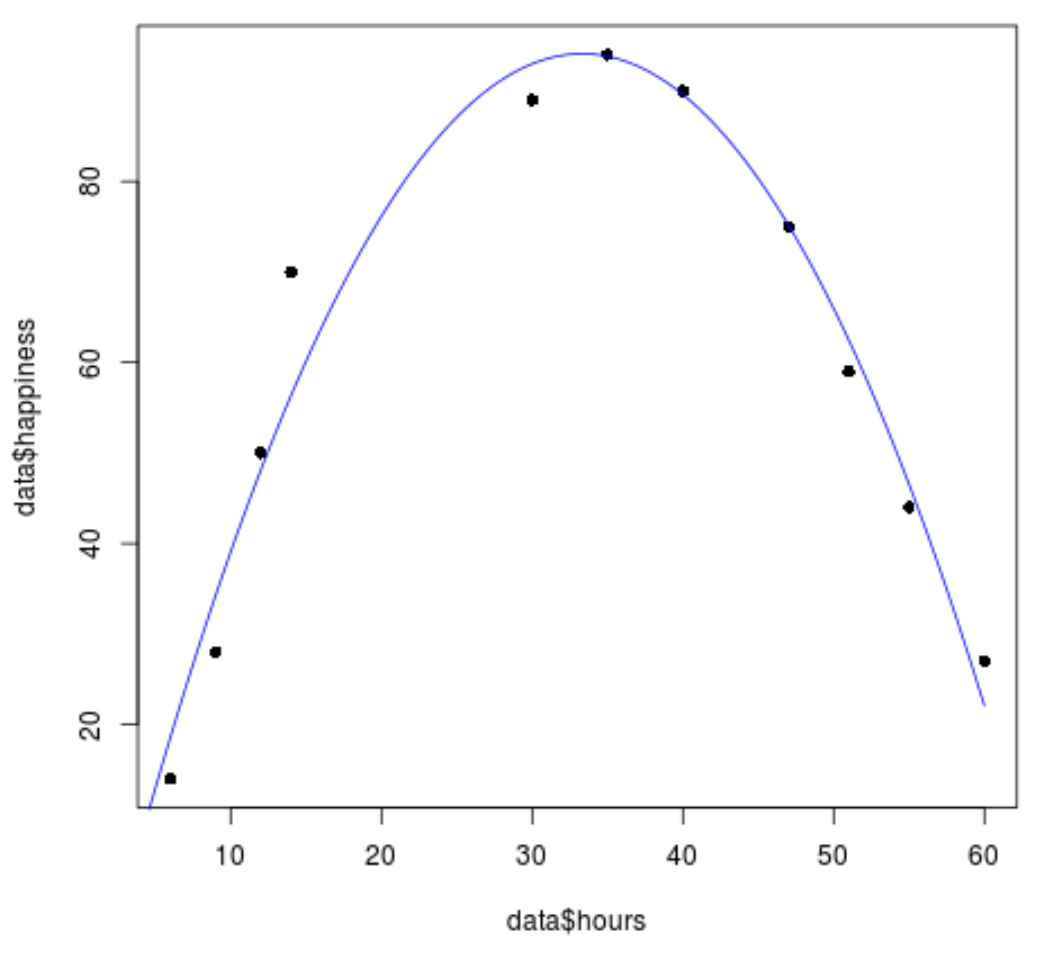
हम देख सकते हैं कि द्विघात प्रतिगमन रेखा डेटा मानों को काफी अच्छी तरह से फिट करती है।

चरण 5: द्विघात प्रतिगमन मॉडल की व्याख्या करें।

पिछले चरण में, हमने देखा कि द्विघात प्रतिगमन मॉडल का परिणाम था:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

यहां प्रस्तुत गुणांकों के आधार पर, समायोजित द्विघात प्रतिगमन होगा:

खुशी = -0.1012 (घंटे) ² + 6.7444 (घंटे) – 18.2536

हम इस समीकरण का उपयोग किसी व्यक्ति की अनुमानित खुशी का पता लगाने के लिए कर सकते हैं, यह देखते हुए कि वे प्रति सप्ताह कितने घंटे काम करते हैं।

उदाहरण के लिए, एक व्यक्ति जो प्रति सप्ताह 60 घंटे काम करता है उसकी खुशी का स्तर 22.09 होगा:

ख़ुशी = -0.1012(60) ² + 6.7444(60) – 18.2536 = 22.09

इसके विपरीत, जो व्यक्ति प्रति सप्ताह 30 घंटे काम करता है उसकी खुशी का स्तर 92.99 होना चाहिए:

खुशी = -0.1012(30) ² + 6.7444(30) – 18.2536 = 92.99