पायथन में सहसंबंध मैट्रिक्स कैसे बनाएं

दो चरों के बीच संबंध को मापने का एक तरीका पियर्सन सहसंबंध गुणांक का उपयोग करना है, जो दो चरों के बीच रैखिक संबंध का एक माप है ।

यह -1 और 1 के बीच का मान लेता है जहां:

• -1 पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है।
• 0 कोई रैखिक सहसंबंध नहीं दर्शाता है।
• 1 पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है।

सहसंबंध गुणांक शून्य से जितना अधिक होगा, दोनों चरों के बीच संबंध उतना ही मजबूत होगा।

लेकिन कुछ मामलों में, हम चरों के अनेक युग्मों के बीच संबंध को समझना चाहते हैं। इन मामलों में, हम एक सहसंबंध मैट्रिक्स बना सकते हैं, जो एक वर्गाकार तालिका है जो चर के कई जोड़ीदार संयोजनों के बीच सहसंबंध गुणांक दिखाती है।

यह ट्यूटोरियल बताता है कि पायथन में सहसंबंध मैट्रिक्स कैसे बनाएं और व्याख्या करें।

पायथन में सहसंबंध मैट्रिक्स कैसे बनाएं

पायथन में सहसंबंध मैट्रिक्स बनाने के लिए निम्नलिखित चरणों का उपयोग करें।

चरण 1: डेटासेट बनाएं।

 import pandas as pd

data = {'assists': [4, 5, 5, 6, 7, 8, 8, 10],
        'rebounds': [12, 14, 13, 7, 8, 8, 9, 13],
        'points': [22, 24, 26, 26, 29, 32, 20, 14]
        }

df = pd. DataFrame (data, columns=['assists','rebounds','points'])
df

   assist rebound points
0 4 12 22
1 5 14 24
2 5 13 26
3 6 7 26
4 7 8 29
5 8 8 32
6 8 9 20
7 10 13 14

चरण 2: सहसंबंध मैट्रिक्स बनाएं।

 #create correlation matrix
df. corr ()

                assists rebound points
assists 1.000000 -0.244861 -0.329573
rebounds -0.244861 1.000000 -0.522092
points -0.329573 -0.522092 1.000000

#create same correlation matrix with coefficients rounded to 3 decimals 
df. corr (). round (3)
	       assists rebound points
assists 1.000 -0.245 -0.330
rebounds -0.245 1.000 -0.522
points -0.330 -0.522 1.000

चरण 3: सहसंबंध मैट्रिक्स की व्याख्या करें।

तालिका के विकर्ण के साथ सहसंबंध गुणांक सभी 1 के बराबर हैं क्योंकि प्रत्येक चर स्वयं के साथ पूरी तरह से सहसंबद्ध है।

अन्य सभी सहसंबंध गुणांक चर के विभिन्न जोड़ीवार संयोजनों के बीच सहसंबंध को दर्शाते हैं। उदाहरण के लिए:

• सहायता और रिबाउंड के बीच सहसंबंध गुणांक -0.245 है।
• सहायता और अंक के बीच सहसंबंध गुणांक -0.330 है।
• रिबाउंड और पॉइंट के बीच सहसंबंध गुणांक -0.522 है।

चरण 4: सहसंबंध मैट्रिक्स की कल्पना करें (वैकल्पिक)।

आप पांडा में उपलब्ध स्टाइलिंग विकल्पों का उपयोग करके सहसंबंध मैट्रिक्स की कल्पना कर सकते हैं:

 corr = df. corr ()
corr. style . background_gradient (cmap='coolwarm')

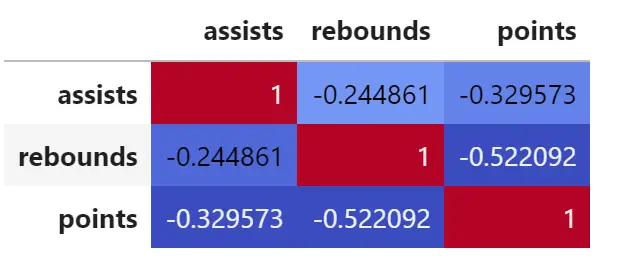
आप विभिन्न रंगों के साथ सहसंबंध मैट्रिक्स बनाने के लिए सीएमएपी तर्क को भी संशोधित कर सकते हैं।

 corr = df. corr ()
corr. style . background_gradient (cmap=' RdYlGn ') 

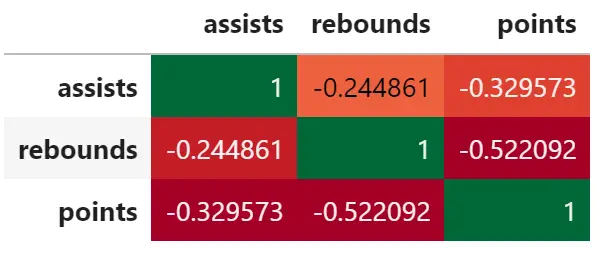
 corr = df. corr ()
corr. style . background_gradient (cmap=' bwr ') 

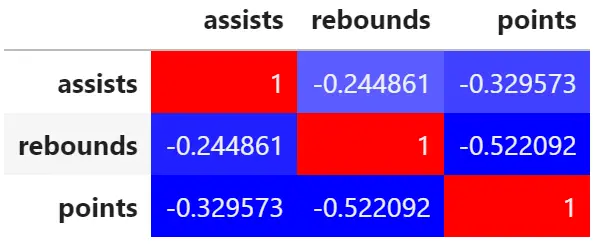
 corr = df. corr ()
corr. style . background_gradient (cmap=' PuOr ') 

नोट : सीएमएपी तर्कों की पूरी सूची के लिए, matplotlib दस्तावेज़ देखें।