सेट पर संचालन: संघ, प्रतिच्छेदन, पूरक और अंतर

समुच्चय तत्वों का एक संग्रह है।

हम एक सेट को बड़े अक्षर से नामित करते हैं और हम घुंघराले ब्रेसिज़ का उपयोग करके सेट के तत्वों को परिभाषित करते हैं। उदाहरण के लिए, मान लीजिए कि हमारे पास “ए” नामक एक सेट है जिसमें तत्व 1, 2, 3 हैं। हम इसे इस प्रकार लिखेंगे:

ए = {1, 2, 3}

यह ट्यूटोरियल संभाव्यता और सांख्यिकी में सबसे अधिक उपयोग किए जाने वाले सेट ऑपरेशनों की व्याख्या करता है।

मिलन

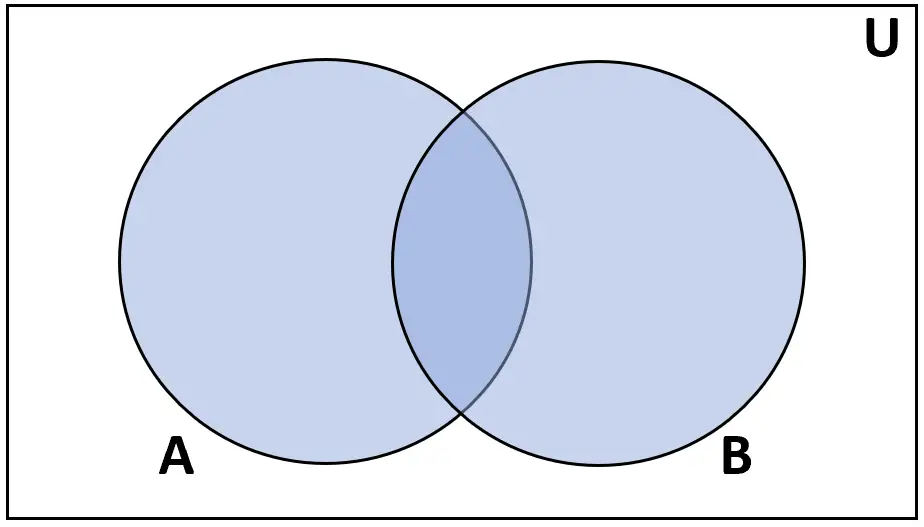
परिभाषा: समुच्चय A और B का मिलन, A या B में पाए जाने वाले तत्वों का समुच्चय है।

रेटिंग: ए ∪ बी

उदाहरण:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

चौराहा

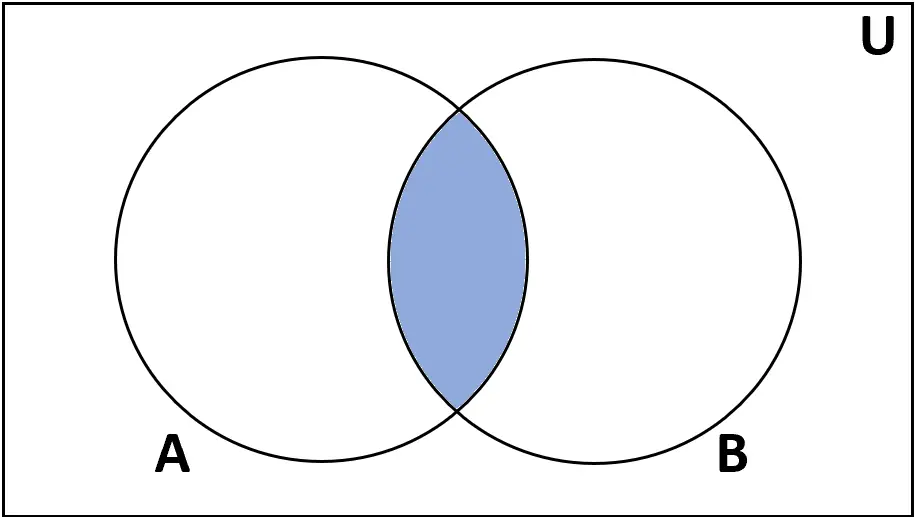
परिभाषा: समुच्चय A और B का प्रतिच्छेदन उन तत्वों का समुच्चय है जो A और B दोनों में पाए जाते हैं।

संकेतन: ए ∩ बी

उदाहरण:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

पूरक

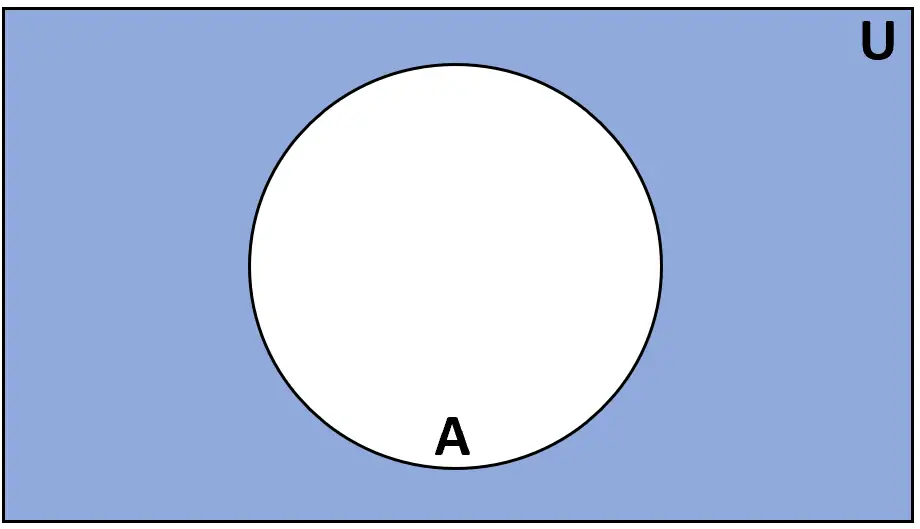
परिभाषा: समुच्चय A का पूरक उन तत्वों का समुच्चय है जो सार्वत्रिक समुच्चय U में हैं लेकिन A में नहीं हैं।

रेटिंग: ए’ या ^एसी

उदाहरण:

• यदि यू = {1, 2, 3, 4, 5, 6} और ए = {1, 2}, तो ए ^सी = {3, 4, 5, 6}
• यदि यू = {1, 2, 3} और ए = {1, 2}, तो ए ^सी = {3}

अंतर

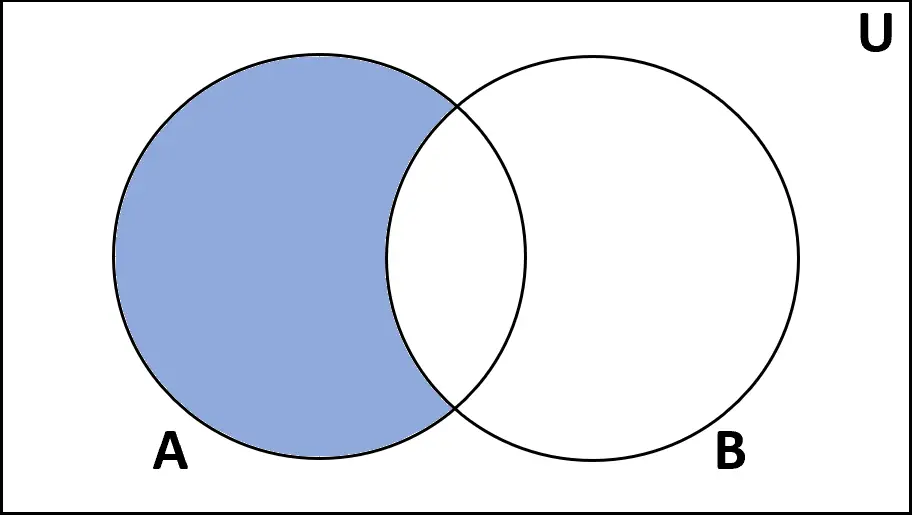
परिभाषा: सेट ए और बी के बीच का अंतर उन तत्वों का सेट है जो ए में पाए जाते हैं लेकिन बी में नहीं।

रेटिंग: ए-बी

उदाहरण:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

सममित अंतर

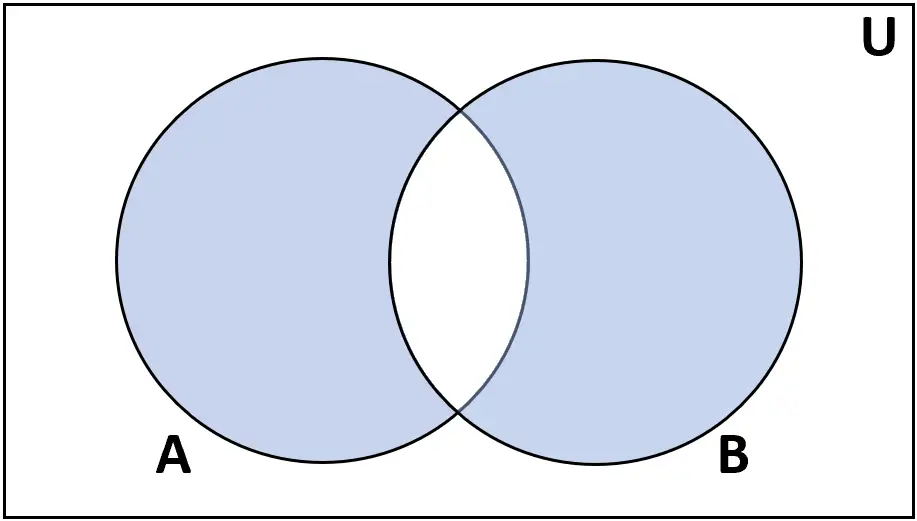
परिभाषा: समुच्चय A और B का सममित अंतर उन तत्वों का समुच्चय है जो A या B में पाए जाते हैं, लेकिन दोनों में नहीं।

रेटिंग: AΔB

उदाहरण:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

कार्तीय गुणन

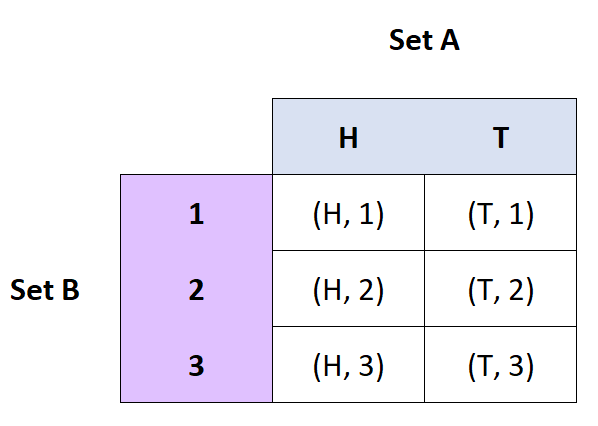
परिभाषा: समुच्चय A और B का कार्तीय गुणनफल, A और B के क्रमित युग्मों का समुच्चय है।

रेटिंग: ए एक्स बी

उदाहरण:

• यदि A = {H, T} और B = {1, 2, 3}, तो A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( टी, 2), (टी, 3)}
• यदि A = {T, H} और B = {1, 2, 3}, तो A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( एच, 2), (एच, 3)}