के-मीन्स क्लस्टरिंग इन आर: चरण-दर-चरण उदाहरण

क्लस्टरिंग एक मशीन लर्निंग तकनीक है जो डेटा सेट के भीतर अवलोकनों के समूहों को खोजने का प्रयास करती है।

लक्ष्य ऐसे समूहों को ढूंढना है कि प्रत्येक क्लस्टर के भीतर अवलोकन एक-दूसरे के समान हों, जबकि विभिन्न समूहों में अवलोकन एक-दूसरे से काफी भिन्न हों।

क्लस्टरिंग बिना पर्यवेक्षित शिक्षण का एक रूप है क्योंकि हम केवल प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के बजाय डेटा सेट के भीतर संरचना खोजने की कोशिश कर रहे हैं।

क्लस्टरिंग का उपयोग अक्सर विपणन में किया जाता है जब व्यवसायों के पास जानकारी तक पहुंच होती है जैसे:

• घरेलू आय
• परिवार का आकार
• घर के मुखिया का पेशा
• निकटतम शहरी क्षेत्र से दूरी

जब यह जानकारी उपलब्ध होती है, तो क्लस्टरिंग का उपयोग उन घरों की पहचान करने के लिए किया जा सकता है जो समान हैं और कुछ उत्पादों को खरीदने या एक निश्चित प्रकार के विज्ञापन पर बेहतर प्रतिक्रिया देने की अधिक संभावना हो सकती है।

क्लस्टरिंग के सबसे सामान्य रूपों में से एक को के-मीन्स क्लस्टरिंग के रूप में जाना जाता है।

K-मीन्स क्लस्टरिंग क्या है?

के-मीन्स क्लस्टरिंग एक ऐसी तकनीक है जिसमें हम डेटासेट से प्रत्येक अवलोकन को के क्लस्टर में से एक में रखते हैं।

अंतिम लक्ष्य K क्लस्टर बनाना है जिसमें प्रत्येक क्लस्टर के भीतर अवलोकन एक-दूसरे के समान होते हैं जबकि विभिन्न समूहों में अवलोकन एक-दूसरे से काफी भिन्न होते हैं।

व्यवहार में, हम K-मीन्स क्लस्टरिंग करने के लिए निम्नलिखित चरणों का उपयोग करते हैं:

1. K के लिए एक मान चुनें.

• सबसे पहले, हमें यह तय करना होगा कि हम डेटा में कितने समूहों की पहचान करना चाहते हैं। अक्सर हमें K के लिए कई अलग-अलग मानों का परीक्षण करने और परिणामों का विश्लेषण करने की आवश्यकता होती है ताकि यह देखा जा सके कि किसी समस्या के लिए कौन से क्लस्टर सबसे अधिक उपयुक्त लगते हैं।

2. 1 से K तक, प्रत्येक अवलोकन को यादृच्छिक रूप से प्रारंभिक क्लस्टर में निर्दिष्ट करें।

3. निम्नलिखित प्रक्रिया तब तक करें जब तक क्लस्टर असाइनमेंट बदलना बंद न हो जाए।

• प्रत्येक K क्लस्टर के लिए, क्लस्टर के गुरुत्वाकर्षण के केंद्र की गणना करें। यह केवल केवें क्लस्टर के अवलोकनों के लिए पी- माध्य विशेषताओं का वेक्टर है।
• प्रत्येक अवलोकन को निकटतम केन्द्रक वाले क्लस्टर में निर्दिष्ट करें। यहां, यूक्लिडियन दूरी का उपयोग करके निकटतम को परिभाषित किया गया है।

के-मीन्स आर में क्लस्टरिंग

निम्नलिखित ट्यूटोरियल आर में के-मीन्स क्लस्टरिंग कैसे करें इसका चरण-दर-चरण उदाहरण प्रदान करता है।

चरण 1: आवश्यक पैकेज लोड करें

सबसे पहले, हम दो पैकेज लोड करेंगे जिनमें आर में के-मीन्स क्लस्टरिंग के लिए कई उपयोगी फ़ंक्शन होंगे।

 library (factoextra)
library (cluster)

चरण 2: डेटा लोड करें और तैयार करें

इस उदाहरण के लिए, हम आर में निर्मित यूएसएरेस्ट्स डेटासेट का उपयोग करेंगे, जिसमें 1973 में प्रत्येक अमेरिकी राज्य में हत्या , हमले और बलात्कार के लिए प्रति 100,000 लोगों पर गिरफ्तारियों की संख्या, साथ ही प्रत्येक राज्य की शहरी आबादी का प्रतिशत शामिल है। क्षेत्र. , अर्बनपॉप ।

निम्नलिखित कोड दिखाता है कि निम्नलिखित कैसे करें:

• यूएसएअरेस्ट डेटासेट लोड करें
• लुप्त मानों वाली सभी पंक्तियाँ हटाएँ
• डेटासेट में प्रत्येक चर को 0 के माध्य और 1 के मानक विचलन के साथ स्केल करें

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

चरण 3: समूहों की इष्टतम संख्या ज्ञात करें

R में k-मीन्स क्लस्टरिंग करने के लिए, हम अंतर्निहित kmeans() फ़ंक्शन का उपयोग कर सकते हैं, जो निम्नलिखित सिंटैक्स का उपयोग करता है:

केमीन्स (डेटा, केंद्र, एनस्टार्ट)

सोना:

• डेटा: डेटासेट का नाम.
• केंद्र: समूहों की संख्या, जिसे k दर्शाया गया है।
• nstart: प्रारंभिक कॉन्फ़िगरेशन की संख्या। चूंकि यह संभव है कि अलग-अलग प्रारंभिक शुरुआती क्लस्टर अलग-अलग परिणाम देंगे, इसलिए कई अलग-अलग प्रारंभिक कॉन्फ़िगरेशन का उपयोग करने की अनुशंसा की जाती है। के-मीन्स एल्गोरिदम प्रारंभिक कॉन्फ़िगरेशन ढूंढेगा जो क्लस्टर के भीतर सबसे छोटी भिन्नता का कारण बनता है।

चूँकि हम पहले से नहीं जानते कि कितने क्लस्टर इष्टतम हैं, हम दो अलग-अलग ग्राफ़ बनाएंगे जो हमें निर्णय लेने में मदद कर सकते हैं:

1. वर्गों के योग के सापेक्ष समूहों की संख्या

सबसे पहले, हम वर्गों की कुल संख्या बनाम समूहों की संख्या का एक प्लॉट बनाने के लिए fviz_nbclust() फ़ंक्शन का उपयोग करेंगे:

 fviz_nbclust(df, kmeans, method = “ wss ”) 

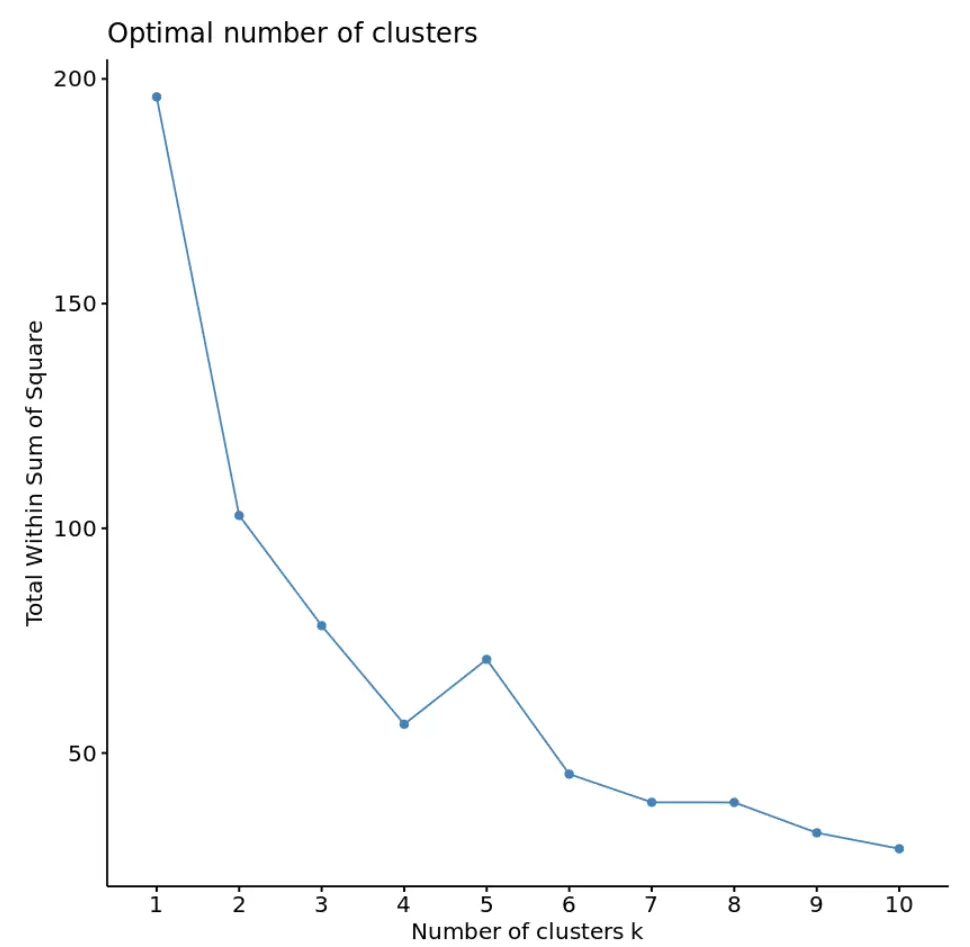
आमतौर पर, जब हम इस प्रकार का प्लॉट बनाते हैं, तो हम एक “घुटने” की तलाश करते हैं जहां वर्गों का योग “झुकना” या समतल होना शुरू हो जाता है। यह आम तौर पर समूहों की इष्टतम संख्या है।

इस ग्राफ़ के लिए, ऐसा प्रतीत होता है कि k = 4 समूहों पर एक छोटा सा मोड़ या “मोड़” है।

2. समूहों की संख्या बनाम अंतराल आँकड़े

समूहों की इष्टतम संख्या निर्धारित करने का एक अन्य तरीका विचलन सांख्यिकी नामक एक मीट्रिक का उपयोग करना है, जो क्लस्टरिंग के बिना वितरण के लिए उनके अपेक्षित मूल्यों के साथ k के विभिन्न मूल्यों के लिए कुल इंट्रा-क्लस्टर भिन्नता की तुलना करता है।

हम क्लस्टर पैकेज से clusGap() फ़ंक्शन का उपयोग करके क्लस्टर की प्रत्येक संख्या के लिए अंतराल आंकड़ों की गणना कर सकते हैं और साथ ही fviz_gap_stat() फ़ंक्शन का उपयोग करके अंतराल आंकड़ों के विरुद्ध क्लस्टर को प्लॉट कर सकते हैं:

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

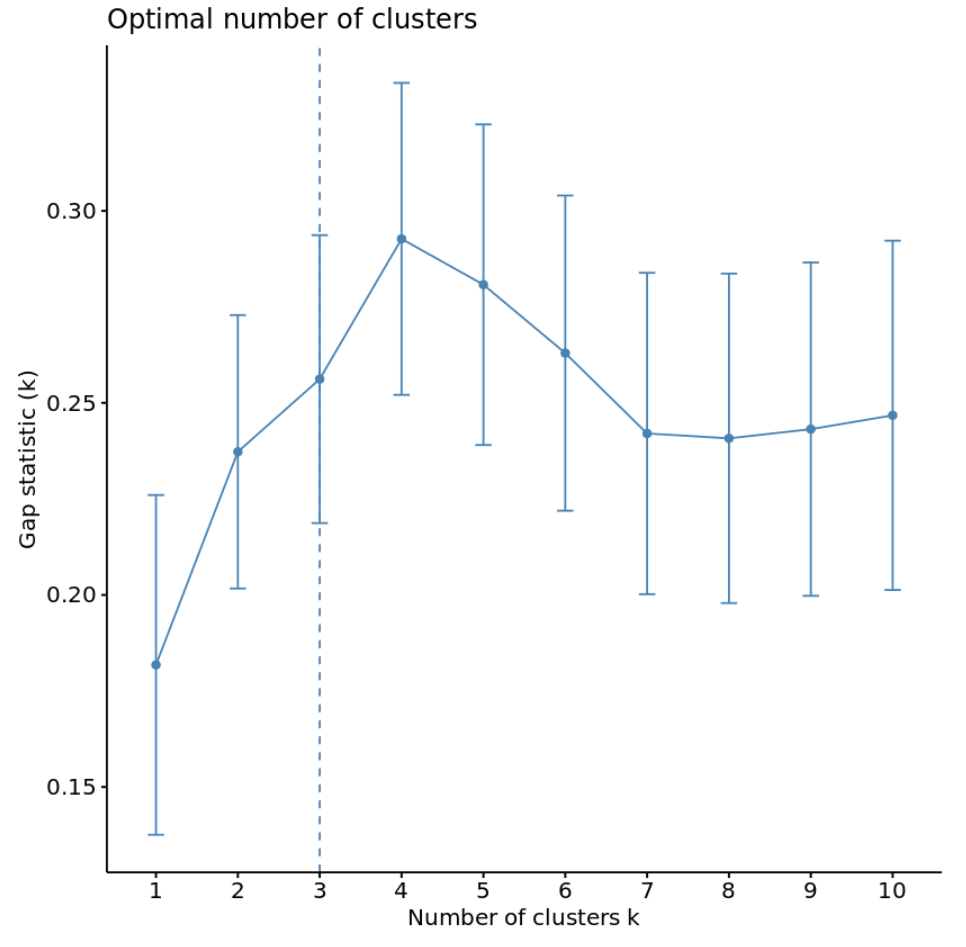
ग्राफ़ से, हम देख सकते हैं कि अंतराल आँकड़ा k = 4 समूहों पर सबसे अधिक है, जो कि हमारे द्वारा पहले इस्तेमाल की गई कोहनी विधि से मेल खाता है।

चरण 4: ऑप्टिमल K के साथ K-मीन्स क्लस्टरिंग करें

अंत में, हम 4 में से k के लिए इष्टतम मान का उपयोग करके डेटासेट पर k-मीन्स क्लस्टरिंग कर सकते हैं:

 #make this example reproducible
set.seed(1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

परिणामों से हम देख सकते हैं कि:

• पहले क्लस्टर को 16 राज्यों को सौंपा गया था
• दूसरे क्लस्टर को 13 राज्यों को सौंपा गया है
• तीसरे क्लस्टर को 13 राज्यों को सौंपा गया है
• चौथे क्लस्टर को 8 राज्यों को सौंपा गया है

हम एक स्कैटरप्लॉट पर क्लस्टर की कल्पना कर सकते हैं जो fivz_cluster() फ़ंक्शन का उपयोग करके अक्षों पर पहले दो प्रमुख घटकों को प्रदर्शित करता है:

 #plot results of final k-means model
fviz_cluster(km, data = df)

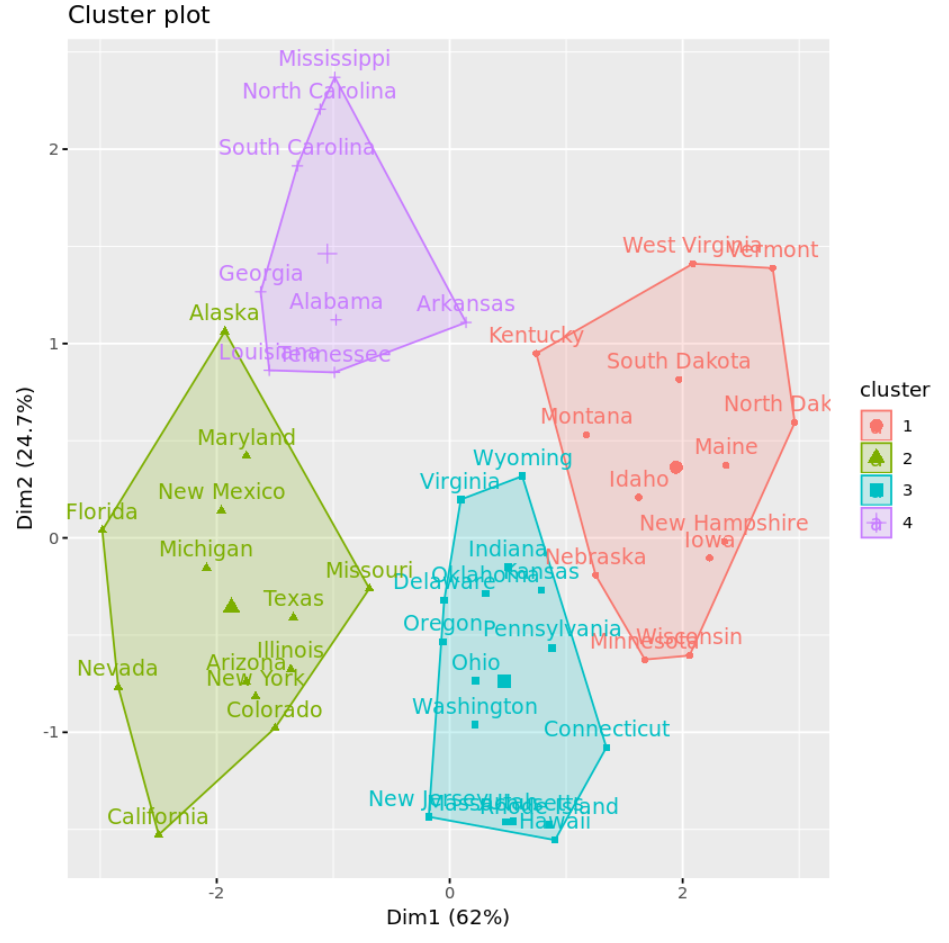
हम प्रत्येक क्लस्टर में चर का औसत ज्ञात करने के लिए एग्रीगेट() फ़ंक्शन का भी उपयोग कर सकते हैं:

 #find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)

cluster Murder Assault UrbanPop Rape
				
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250

हम इस आउटपुट की व्याख्या इस प्रकार करते हैं:

• समूह 1 के राज्यों में प्रति 100,000 नागरिकों पर हत्याओं की औसत संख्या 3.6 है।
• समूह 1 के राज्यों में प्रति 100,000 नागरिकों पर हमलों की औसत संख्या 78.5 है।
• समूह 1 राज्यों में शहरी क्षेत्र में रहने वाले निवासियों का औसत प्रतिशत 52.1% है।
• समूह 1 के राज्यों में प्रति 100,000 नागरिकों पर बलात्कार की औसत संख्या 12.2 है ।

और इसी तरह।

हम प्रत्येक राज्य के क्लस्टर असाइनमेंट को मूल डेटासेट में भी जोड़ सकते हैं:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

के-मीन्स क्लस्टरिंग के फायदे और नुकसान

K-मीन्स क्लस्टरिंग निम्नलिखित लाभ प्रदान करता है:

• यह एक तेज़ एल्गोरिदम है.
• यह बड़े डेटासेट को अच्छे से संभाल सकता है।

हालाँकि, इसके निम्नलिखित संभावित नुकसान हैं:

• इसके लिए हमें एल्गोरिदम चलाने से पहले क्लस्टर की संख्या निर्दिष्ट करने की आवश्यकता है।
• यह आउटलेर्स के प्रति संवेदनशील है।

के-मीन्स क्लस्टरिंग के दो विकल्प हैं के-मीन्स क्लस्टरिंग और पदानुक्रमित क्लस्टरिंग।

आप इस उदाहरण में प्रयुक्त पूरा आर कोड यहां पा सकते हैं।