R में dfbetas की गणना कैसे करें

आंकड़ों में, हम अक्सर जानना चाहते हैं कि प्रतिगमन मॉडल में विभिन्न अवलोकनों का क्या प्रभाव पड़ता है।

अवलोकनों के प्रभाव की गणना करने का एक तरीका डीएफबीईटीएएस नामक मीट्रिक का उपयोग करना है, जो हमें प्रत्येक व्यक्तिगत अवलोकन को हटाने के प्रत्येक गुणांक पर मानकीकृत प्रभाव बताता है।

यह मीट्रिक हमें किसी दिए गए प्रतिगमन मॉडल में प्रत्येक गुणांक अनुमान पर प्रत्येक अवलोकन के प्रभाव का एक विचार देता है।

यह ट्यूटोरियल आर में एक मॉडल में प्रत्येक अवलोकन के लिए डीएफबीईटीएएस की गणना और कल्पना करने का चरण-दर-चरण उदाहरण दिखाता है।

चरण 1: एक प्रतिगमन मॉडल बनाएं

सबसे पहले, हम R में निर्मित mtcars डेटासेट का उपयोग करके एक बहु रेखीय प्रतिगमन मॉडल बनाएंगे:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

चरण 2: प्रत्येक अवलोकन के लिए DFBETAS की गणना करें

इसके बाद, हम मॉडल में प्रत्येक अवलोकन के लिए DFBETAS मानों की गणना करने के लिए अंतर्निहित dfbetas() फ़ंक्शन का उपयोग करेंगे:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

प्रत्येक अवलोकन के लिए, हम मूल, डिस्प वेरिएबल और एचपी वेरिएबल के लिए गुणांक अनुमान में अंतर देख सकते हैं जो तब होता है जब हम उस विशेष अवलोकन को हटाते हैं।

आम तौर पर, हम मानते हैं कि किसी अवलोकन का किसी दिए गए गुणांक के अनुमान पर एक मजबूत प्रभाव पड़ता है यदि इसका DBETAS मान 2/√ n की सीमा से अधिक है जहां n अवलोकनों की संख्या है।

इस उदाहरण में, सीमा 0.3535534 होगी:

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

चरण 3: DFBETAS की कल्पना करें

अंत में, हम मॉडल में प्रत्येक अवलोकन और प्रत्येक भविष्यवक्ता के लिए DFBETAS मान की कल्पना करने के लिए प्लॉट बना सकते हैं:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

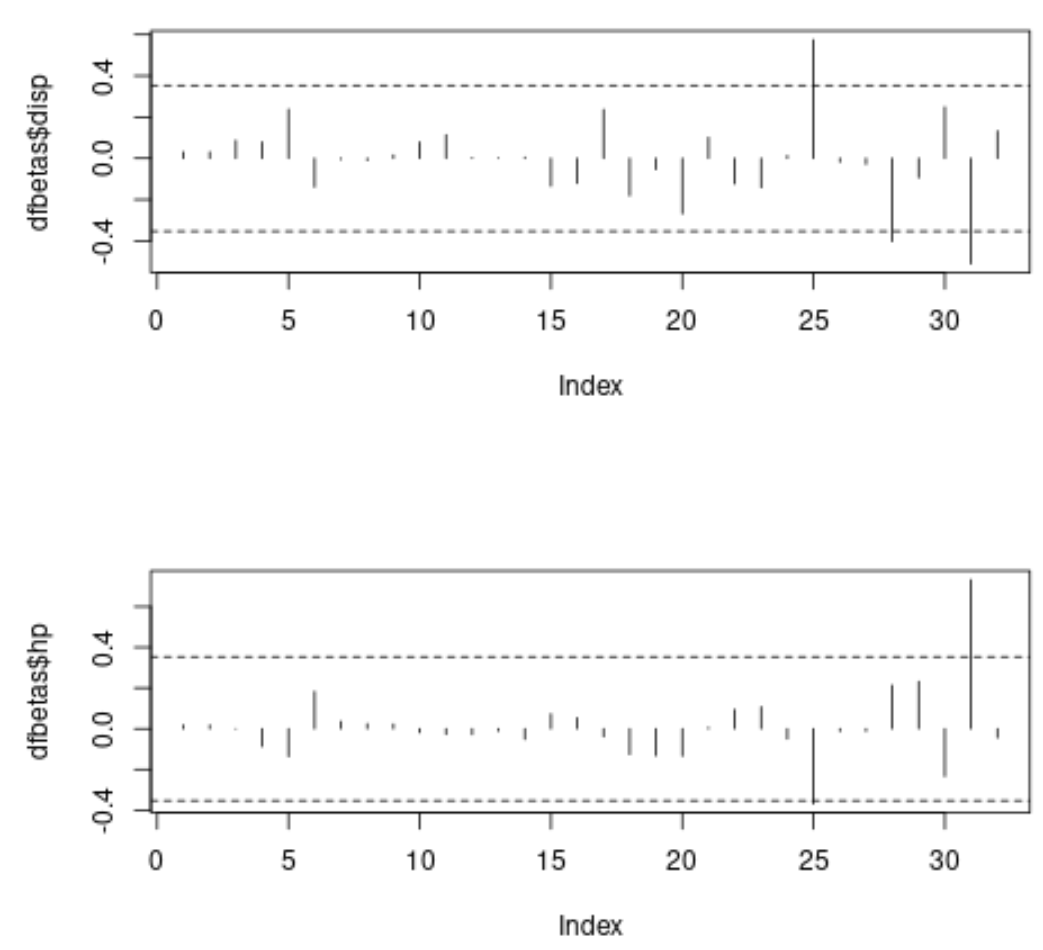
प्रत्येक प्लॉट में, x-अक्ष डेटासेट में प्रत्येक अवलोकन के सूचकांक को प्रदर्शित करता है और y-मान प्रत्येक अवलोकन और प्रत्येक भविष्यवक्ता के लिए संबंधित DFBETAS प्रदर्शित करता है।

पहले प्लॉट पर हम देख सकते हैं कि तीन अवलोकन 0.3535534 के पूर्ण थ्रेशोल्ड मान से अधिक हैं और दूसरे प्लॉट पर हम देख सकते हैं कि दो अवलोकन निरपेक्ष थ्रेशोल्ड मान से अधिक हैं।

हम यह निर्धारित करने के लिए इन अवलोकनों का अधिक बारीकी से अध्ययन करना चुन सकते हैं कि क्या मॉडल गुणांक के अनुमान पर उनका अनुचित प्रभाव है।

अतिरिक्त संसाधन

आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में उत्तोलन आँकड़ों की गणना कैसे करें
आर में डीएफएफआईटीएस की गणना कैसे करें