Google शीट्स में z स्कोर की गणना कैसे करें
आंकड़ों में, एक z-स्कोर हमें बताता है कि एक मान माध्य से कितने मानक विचलन है । हम z-स्कोर की गणना के लिए निम्नलिखित सूत्र का उपयोग करते हैं:
z = (एक्स – μ) / σ
सोना:
- X एकल कच्चा डेटा मान है
- μ डेटा सेट का माध्य है
- σ डेटासेट का मानक विचलन है
यह ट्यूटोरियल बताता है कि Google शीट्स में कच्चे डेटा मानों के लिए z-स्कोर की गणना कैसे करें।
उदाहरण: Google शीट्स में z-स्कोर
मान लीजिए कि हमारे पास निम्नलिखित डेटा सेट है और हम प्रत्येक कच्चे डेटा मान के लिए z-स्कोर खोजना चाहते हैं:
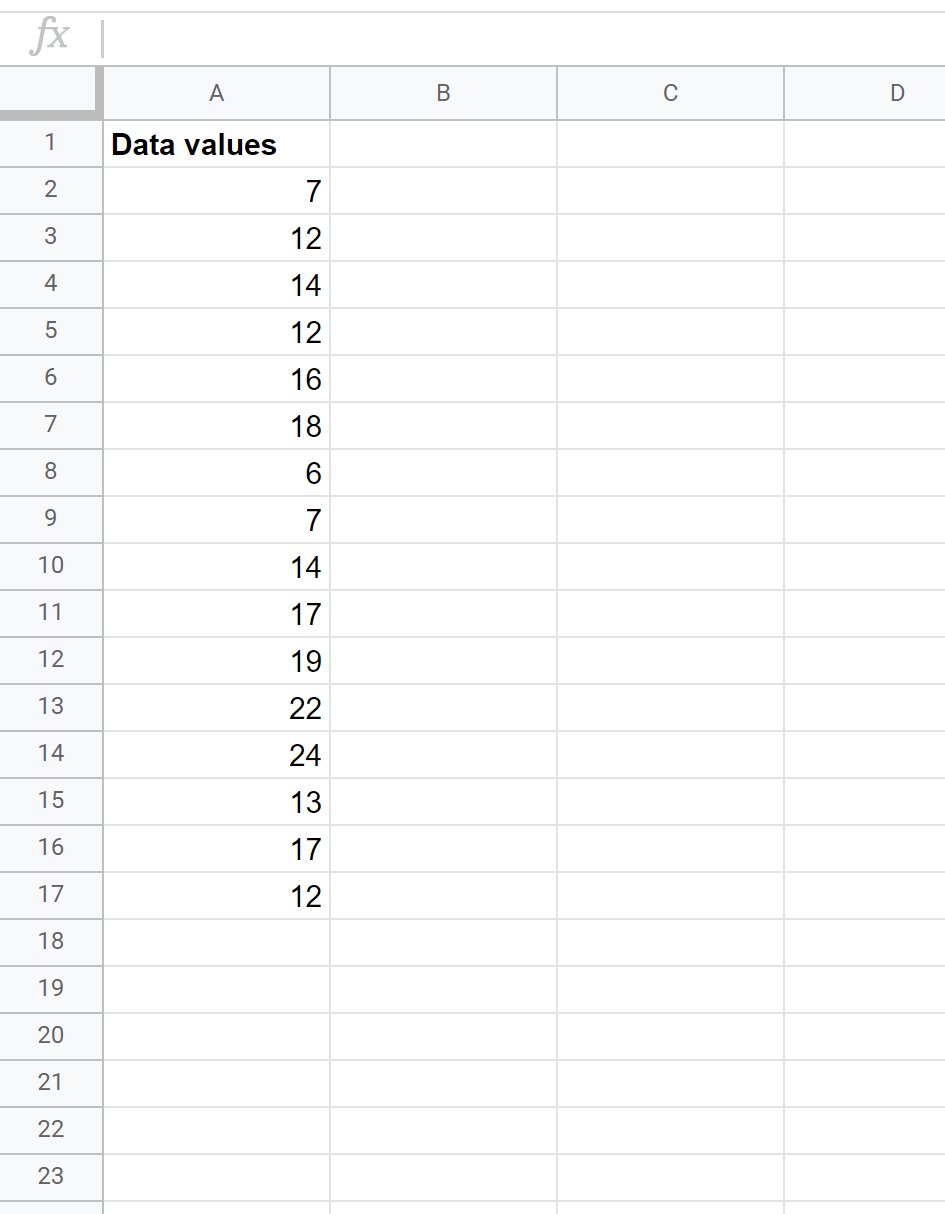
ऐसा करने के लिए हम निम्नलिखित कदम उठा सकते हैं।
चरण 1: डेटा सेट का माध्य और मानक विचलन ज्ञात करें।
सबसे पहले, हमें डेटासेट का माध्य और मानक विचलन ज्ञात करना होगा। निम्नलिखित सूत्र बताते हैं कि यह कैसे करना है:
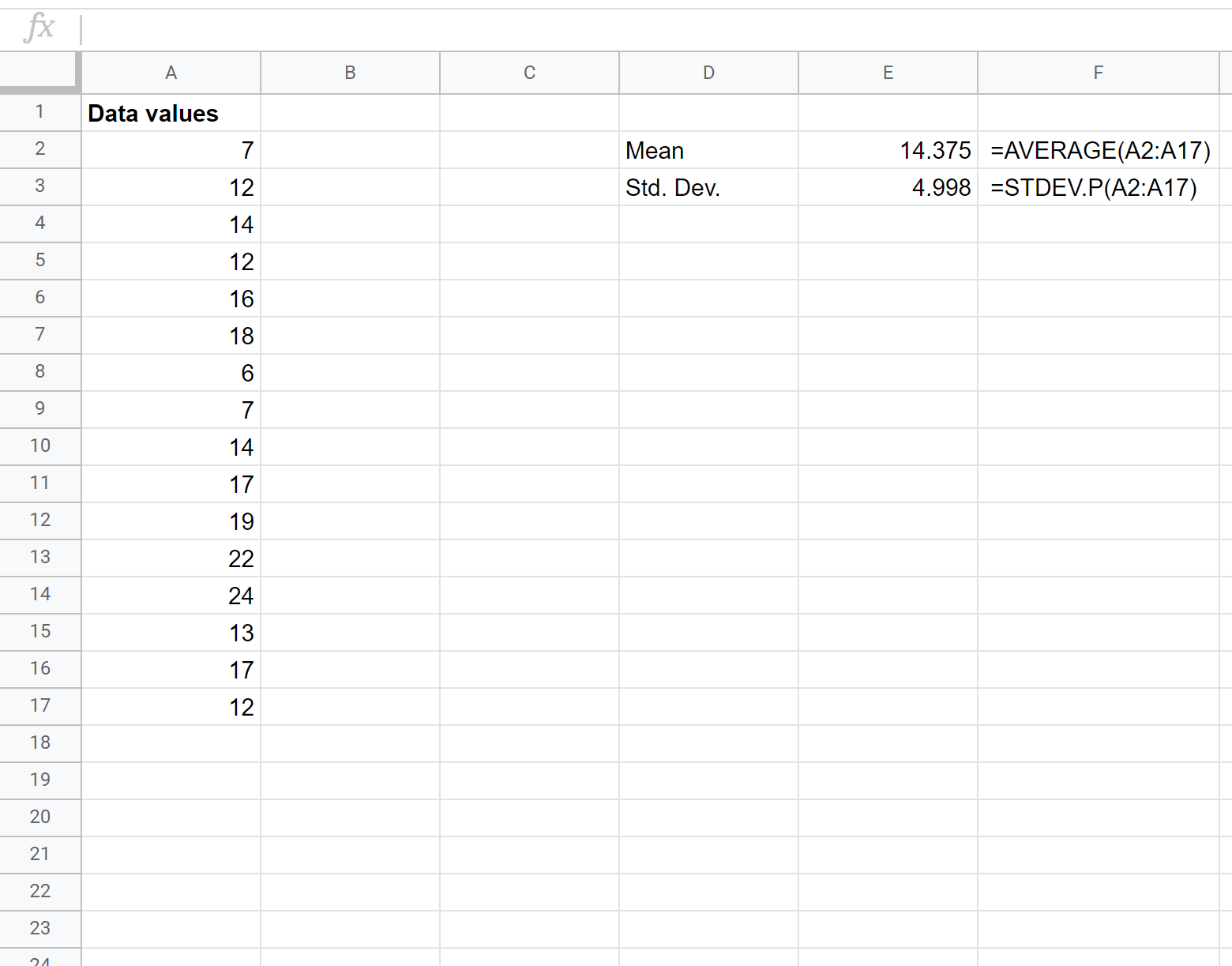
माध्य 14.375 है और मानक विचलन 4.998 है।
चरण 2: पहले कच्चे डेटा मान के लिए z-स्कोर खोजें।
इसके बाद, हम सेल B2 में निम्नलिखित सूत्र टाइप करके पहले कच्चे डेटा मान के लिए z-स्कोर पाएंगे:
= ( ए2 – $ई$2 ) / $ई$3
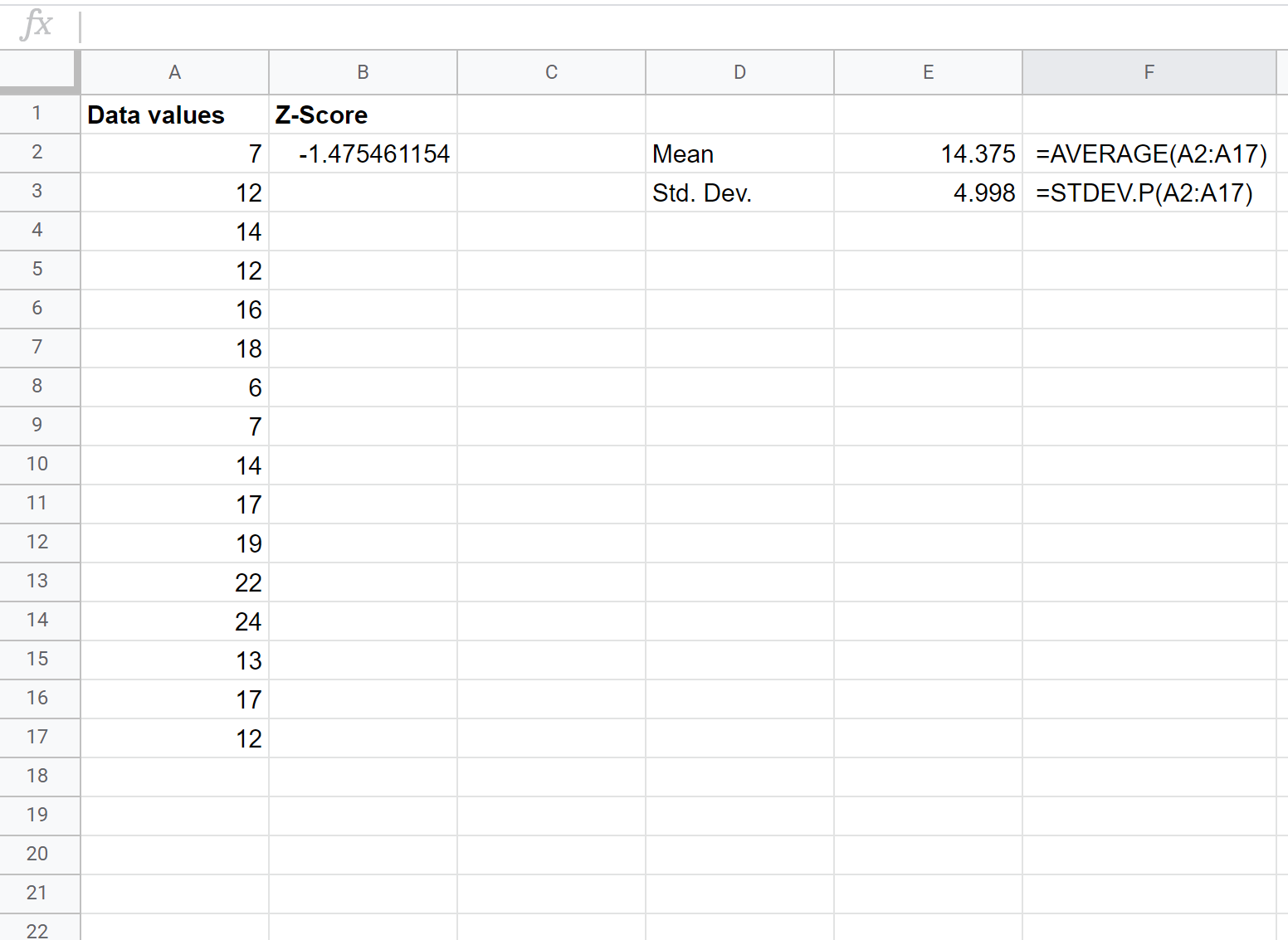
चरण 3: शेष सभी मानों के लिए z-स्कोर ज्ञात करें।
एक बार जब हम पहले z-स्कोर की गणना कर लेते हैं, तो हम सेल B2 से शुरू करके शेष कॉलम B को हाइलाइट कर सकते हैं और सेल B2 से नीचे दिए गए प्रत्येक सेल में फॉर्मूला कॉपी करने के लिए Ctrl+D दबा सकते हैं:
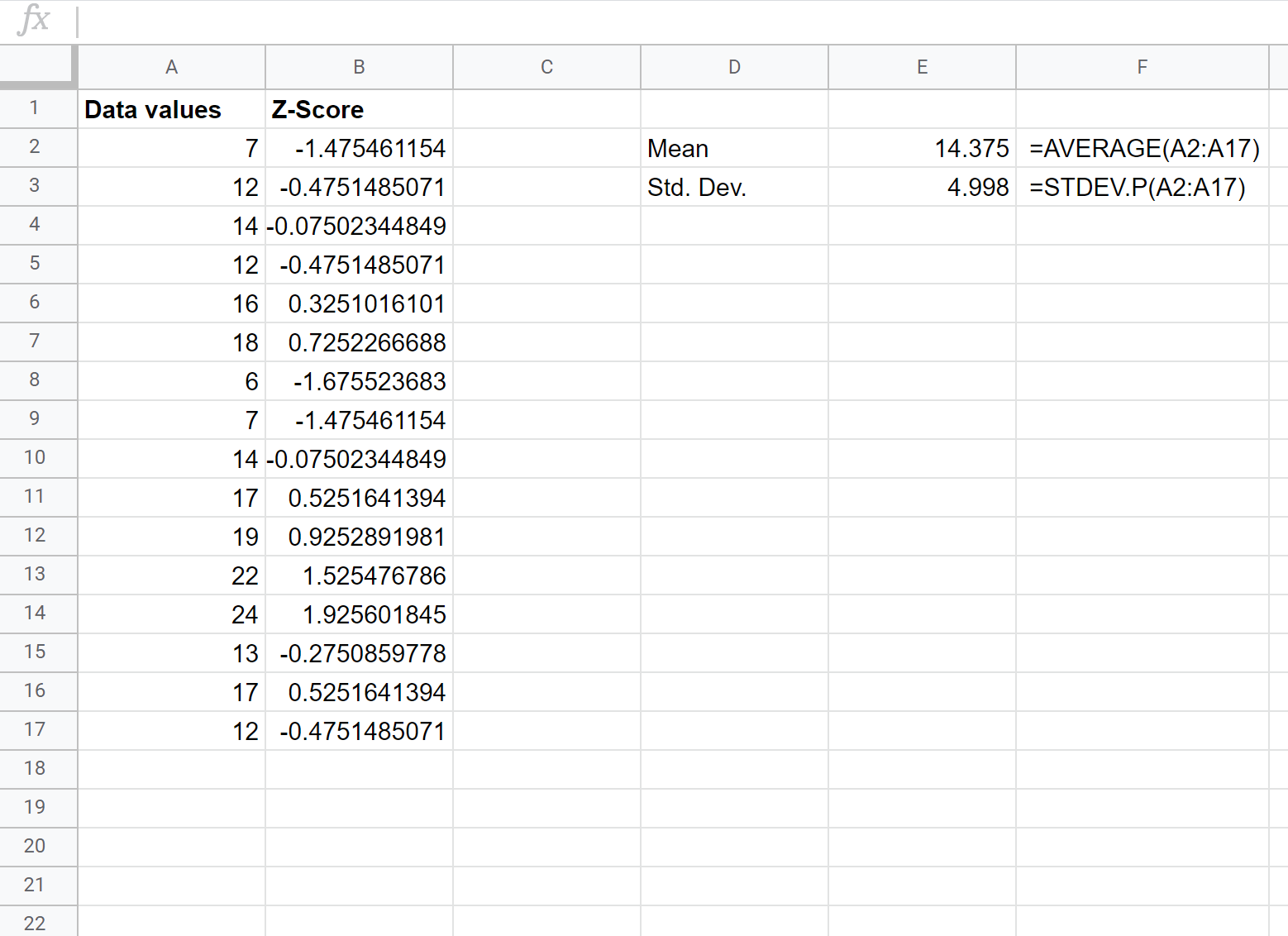
अब हमें प्रत्येक कच्चे डेटा मान के लिए z-स्कोर मिल गया है।
Z स्कोर की व्याख्या कैसे करें
एक z-स्कोर हमें बस यह बताता है कि एक मान माध्य से कितने मानक विचलन है।
हमारे उदाहरण में, हमने पाया कि माध्य 14.375 था और मानक विचलन 4.998 था।
तो हमारे डेटासेट में पहला मान 7 था, जिसका z-स्कोर (7-14.375) / 4.998 = -1.47546 था। इसका मतलब है कि मान “7” माध्य से -1.47545 मानक विचलन कम है।
हमारे डेटा में अगला मान, 12, का z-स्कोर (12-14.375) / 4.998 = -0.47515 था। इसका मतलब है कि मान “12” माध्य से -0.47515 मानक विचलन कम है।
कोई मान माध्य से जितना दूर होगा, उस मान के लिए z-स्कोर का निरपेक्ष मान उतना ही अधिक होगा। उदाहरण के लिए, मान 7, मान 12 की तुलना में माध्य (14.375) से अधिक है, जो बताता है कि 7 में बड़े निरपेक्ष मान के साथ z-स्कोर क्यों था।
अतिरिक्त संसाधन
एक्सेल में Z स्कोर की गणना कैसे करें
R में Z स्कोर की गणना कैसे करें
TI-84 कैलकुलेटर पर Z स्कोर की गणना कैसे करें
लेखक के बारे में
डॉ. बेंजामिन एंडरसन
नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने