Z तालिका का उपयोग कैसे करें (उदाहरण के साथ)

A z तालिका एक तालिका है जो आपको बताती है कि मानक सामान्य वितरण में कितने प्रतिशत मान एक निश्चित z स्कोर से नीचे आते हैं।

एक z-स्कोर बस आपको बताता है कि एक व्यक्तिगत डेटा मान माध्य से कितने मानक विचलन करता है। इसकी गणना इस प्रकार की जाती है:

z-स्कोर = (x – μ) / σ

सोना:

• x: व्यक्तिगत डेटा मान
• μ: जनसंख्या औसत
• σ: जनसंख्या मानक विचलन

यह ट्यूटोरियल z तालिका का उपयोग करने के कई उदाहरण दिखाता है।

उदाहरण 1

एक निश्चित कॉलेज प्रवेश परीक्षा के अंक आम तौर पर माध्य μ = 82 और मानक विचलन σ = 8 के साथ वितरित किए जाते हैं। परीक्षा में लगभग कितने प्रतिशत छात्र 84 से नीचे अंक प्राप्त करते हैं?

चरण 1: z-स्कोर ज्ञात करें।

सबसे पहले, हम 84 के परीक्षा स्कोर से जुड़े ज़ेड-स्कोर का पता लगाएंगे:

z-स्कोर = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0.25

चरण 2: z स्कोर के अनुरूप प्रतिशत ज्ञात करने के लिए z चार्ट का उपयोग करें।

इसके बाद, हम z तालिका में मान 0.25 देखेंगे:

इस परीक्षा में लगभग 59.87% छात्रों का स्कोर 84 से कम है।

उदाहरण 2

एक निश्चित बगीचे में पौधों की ऊंचाई आम तौर पर μ = 26.5 इंच के औसत और σ = 2.5 इंच के मानक विचलन के साथ वितरित की जाती है। लगभग कितने प्रतिशत पौधे 26 इंच से अधिक लम्बे हैं?

चरण 1: z-स्कोर ज्ञात करें।

सबसे पहले, हम 26 इंच की ऊंचाई से जुड़े ज़ेड-स्कोर को ढूंढेंगे।

z-स्कोर = (x – μ) / σ = (26 – 26.5) / 2.5 = -0.5 / 2.5 = -0.2

चरण 2: z स्कोर के अनुरूप प्रतिशत ज्ञात करने के लिए z चार्ट का उपयोग करें।

आगे हम मान -0.2 देखेंगे   तालिका z में:

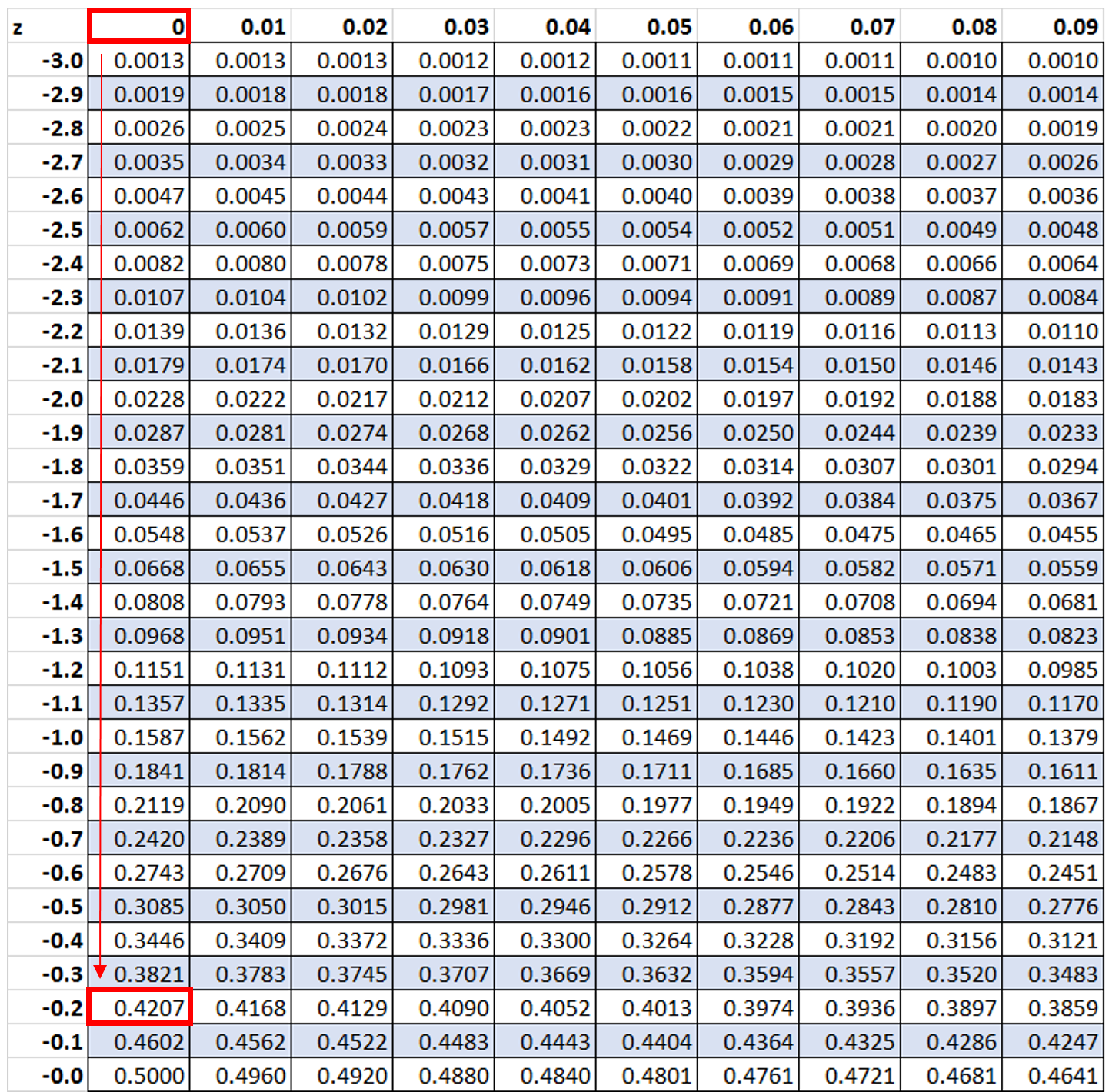
हम देखते हैं कि 42.07% मान -0.2 के z-स्कोर से नीचे हैं। हालाँकि, इस उदाहरण में हम जानना चाहते हैं कि कितने प्रतिशत मान -0.2 से अधिक हैं, जिसे हम सूत्र 100% – 42.07% = 57.93% का उपयोग करके पा सकते हैं।

तो, इस बगीचे में लगभग 59.87% पौधे 26 इंच से अधिक लम्बे हैं।

उदाहरण 3

एक निश्चित डॉल्फ़िन प्रजाति का वजन आम तौर पर μ = 400 पाउंड के औसत और σ = 25 पाउंड के मानक विचलन के साथ वितरित किया जाता है। लगभग कितने प्रतिशत डॉल्फ़िन का वज़न 410 से 425 पाउंड के बीच होता है?

चरण 1: z-स्कोर खोजें।

सबसे पहले, हम 410 पुस्तकों और 425 पुस्तकों से जुड़े z-स्कोर ढूंढेंगे

410 का z-स्कोर = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0.4

425 का z स्कोर = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

चरण 2: प्रत्येक z स्कोर के अनुरूप प्रतिशत ज्ञात करने के लिए z चार्ट का उपयोग करें।

सबसे पहले, हम मान 0.4 देखेंगे   तालिका z में:

आगे हम मान 1 की तलाश करेंगे   तालिका z में:

अंत में, हम सबसे बड़े मान से सबसे छोटा मान घटा देंगे: 0.8413 – 0.6554 = 0.1859 ।

तो, लगभग 18.59% डॉल्फ़िन का वजन 410 से 425 पाउंड के बीच होता है।

अतिरिक्त संसाधन

सामान्य वितरण का परिचय
सामान्य वितरण क्षेत्र कैलकुलेटर
Z स्कोर कैलकुलेटर