आँकड़ों में z मान और p मान के बीच अंतर

दो शब्द जिन्हें छात्र अक्सर सांख्यिकी में भ्रमित करते हैं, वे हैं z-मान और p-मान ।

इन शब्दों के बीच अंतर को समझने के लिए, z परीक्षणों को समझने में मदद मिलती है।

z परीक्षण के दो सामान्य प्रकार हैं:

• एक-नमूना z-परीक्षण : इसका उपयोग यह परीक्षण करने के लिए किया जाता है कि जनसंख्या माध्य एक निश्चित मान के बराबर है या नहीं।
• दो-नमूना z-परीक्षण : यह परीक्षण करने के लिए उपयोग किया जाता है कि क्या दो जनसंख्या माध्य बराबर हैं।

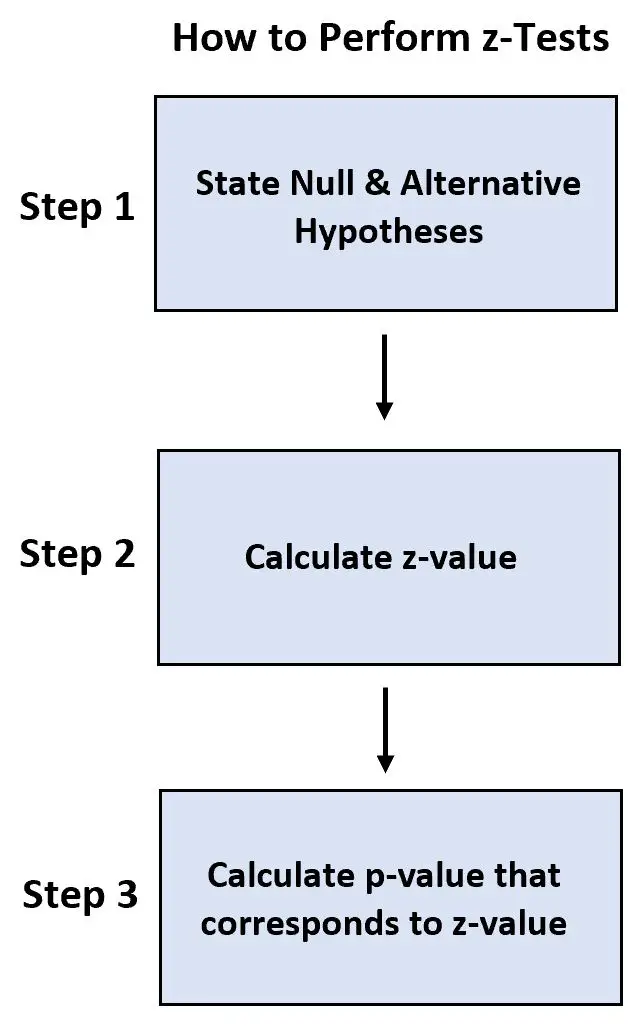
हम प्रत्येक परीक्षण करने के लिए निम्नलिखित चरणों का उपयोग करते हैं:

• चरण 1: शून्य और वैकल्पिक परिकल्पना बताएं।
• चरण 2: z मान की गणना करें।
• चरण 3: उस पी-मान की गणना करें जो z-मान से मेल खाता है।

प्रत्येक परीक्षण के लिए, z-मान जनसंख्या साधनों के बीच अंतर को मापने का एक तरीका है और p-मान कम से कम उतने बड़े निरपेक्ष मान के साथ z-मान प्राप्त करने की संभावना है जितना हमने वास्तव में ‘नमूने में देखा था। यदि शून्य परिकल्पना वास्तव में सत्य है तो डेटा।

यदि पी-मान एक निश्चित मान (जैसे 0.05) से कम है, तो हम परीक्षण की शून्य परिकल्पना को अस्वीकार कर देते हैं ।

प्रत्येक प्रकार के z परीक्षण के लिए, हम p-मान में रुचि रखते हैं और हम p-मान की गणना करने के लिए मध्यवर्ती चरण के रूप में z-मान का उपयोग करते हैं।

निम्नलिखित उदाहरण दिखाता है कि दो-नमूना z-परीक्षण के लिए z-मान और संबंधित p-मान की गणना और व्याख्या कैसे करें।

उदाहरण: Z मान और P मान की गणना और व्याख्या करें

मान लें कि दो अलग-अलग शहरों के व्यक्तियों का आईक्यू स्तर सामान्य रूप से वितरित है, प्रत्येक की जनसंख्या मानक विचलन 15 है।

एक वैज्ञानिक जानना चाहता है कि क्या शहर A और शहर B में व्यक्तियों के बीच औसत IQ स्तर भिन्न है। इसलिए वह प्रत्येक शहर से 20 व्यक्तियों का एक सरल यादृच्छिक नमूना चुनती है और उनके आईक्यू स्तर को रिकॉर्ड करती है:

शहर ए : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

शहर बी : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

इस डेटा का उपयोग करके दो-नमूना z परीक्षण करने का तरीका यहां बताया गया है:

चरण 1: शून्य और वैकल्पिक परिकल्पना बताएं।

सबसे पहले, हम शून्य और वैकल्पिक परिकल्पनाएँ बताएंगे:

• एच ₀ : μ ₁ = μ ₂ (दोनों जनसंख्या माध्य बराबर हैं)
• एच ₁ : μ ₁ ≠ μ ₂ (दोनों जनसंख्या माध्य बराबर नहीं हैं)

चरण 2: z मान की गणना करें।

इसके बाद, हम इस डेटा का उपयोग करके एक्सेल में दो-नमूना z-परीक्षण करेंगे और पाएंगे कि z-मान -1.71817 है।

चरण 3: पी-वैल्यू की गणना करें।

हम यह पता लगाने के लिए Z स्कोर से P मान कैलकुलेटर का उपयोग कर सकते हैं कि -1.71817 के az मान के अनुरूप p मान 0.08577 है।

चूँकि यह पी-मान 0.05 से कम नहीं है, हमारे पास शून्य परिकल्पना को अस्वीकार करने के लिए पर्याप्त सबूत नहीं हैं।

इस प्रकार, हम यह निष्कर्ष निकालते हैं कि दोनों शहरों के बीच औसत आईक्यू स्तर में कोई खास अंतर नहीं है।

ध्यान दें कि हमने p मान की गणना करने के लिए केवल मध्यवर्ती चरण के रूप में z मान का उपयोग किया है।

पी-वैल्यू वह वास्तविक मूल्य है जिसमें हमारी रुचि थी, लेकिन हमें पहले ज़ेड-वैल्यू की गणना करनी थी।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि विभिन्न सांख्यिकीय सॉफ़्टवेयर का उपयोग करके z-परीक्षण कैसे करें:

एक्सेल में Z टेस्ट कैसे करें
R में Z परीक्षण कैसे करें
पायथन में Z टेस्ट कैसे करें