एक्सेल में z स्कोर की गणना कैसे करें

आंकड़ों में, एक z-स्कोर हमें बताता है कि एक मान माध्य से कितने मानक विचलन है। हम z-स्कोर की गणना के लिए निम्नलिखित सूत्र का उपयोग करते हैं:

z = (एक्स – μ) / σ

सोना:

• X एकल कच्चा डेटा मान है
• μ डेटा सेट का माध्य है
• σ डेटासेट का मानक विचलन है

यह ट्यूटोरियल बताता है कि Excel में कच्चे डेटा मानों के लिए z-स्कोर की गणना कैसे करें।

एक्सेल में Z स्कोर की गणना कैसे करें

मान लीजिए कि हमारे पास निम्नलिखित डेटा सेट है और हम प्रत्येक कच्चे डेटा मान के लिए z-स्कोर खोजना चाहते हैं:

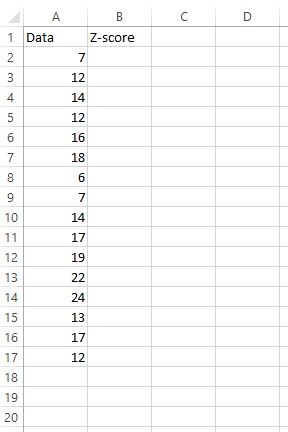
ऐसा करने के लिए हम निम्नलिखित कदम उठा सकते हैं।

चरण 1: डेटा सेट का माध्य और मानक विचलन ज्ञात करें।

सबसे पहले, हमें डेटासेट का माध्य और मानक विचलन ज्ञात करना होगा। निम्नलिखित सूत्र बताते हैं कि यह कैसे करना है:

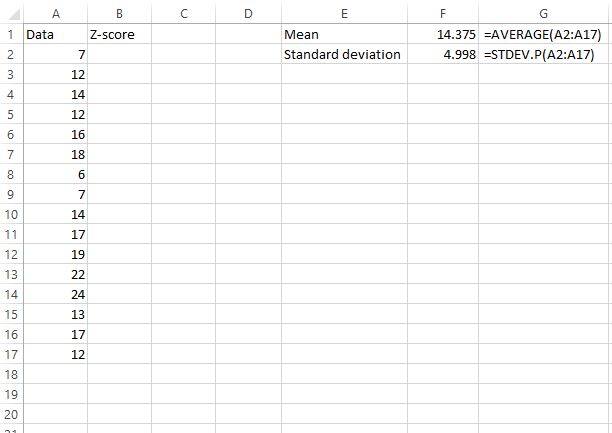
माध्य 14.375 है और मानक विचलन 4.998 है।

चरण 2: पहले कच्चे डेटा मान के लिए z-स्कोर खोजें।

इसके बाद, हम सूत्र z = (X – μ) / σ का उपयोग करके पहले कच्चे डेटा मान के लिए z-स्कोर पाएंगे।

सेल C2 वह सूत्र दिखाता है जिसका उपयोग हमने सेल B2 में z मान की गणना करने के लिए किया था।

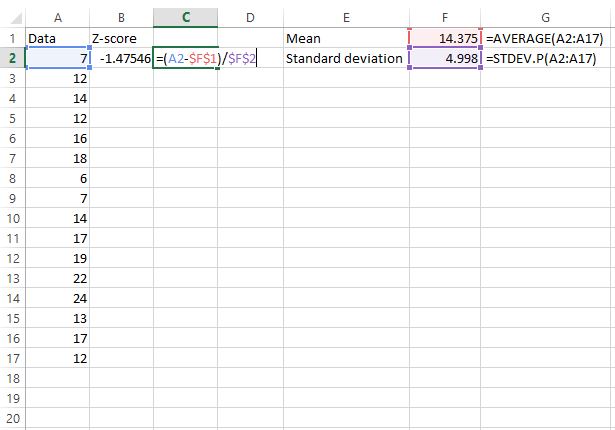
चरण 3: शेष सभी मानों के लिए z-स्कोर ज्ञात करें।

अब जब हमें डेटा सेट में पहले मान के लिए z-स्कोर मिल गया है, तो हम सेल B2 में उपयोग किए गए सूत्र को शेष डेटा मानों में कॉपी कर सकते हैं। हम पूरे z-स्कोर कॉलम को हाइलाइट करके ऐसा कर सकते हैं, पहले z-स्कोर से शुरू करके जिसकी हमने पहले ही गणना कर ली है:

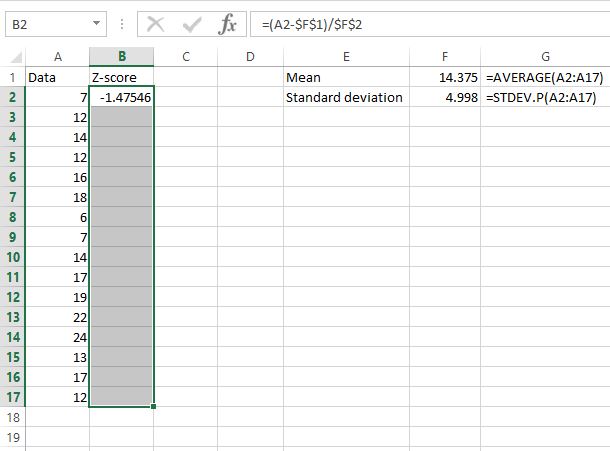
इसके बाद Ctrl+D दबाएं। यह पहली सेल से उसके नीचे की सभी कोशिकाओं में सूत्र की प्रतिलिपि बनाता है।

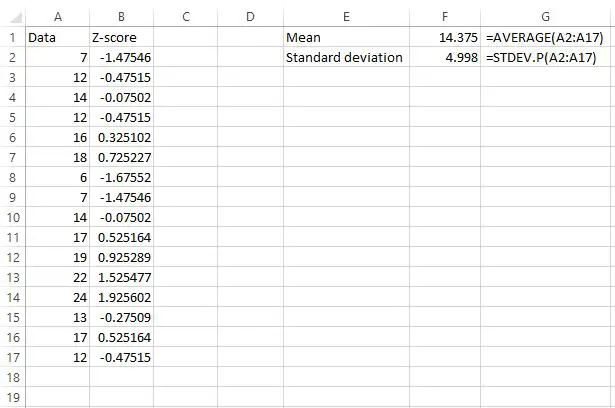
अब हमें प्रत्येक कच्चे डेटा मान के लिए z-स्कोर मिल गया है।

एक्सेल में Z स्कोर की व्याख्या कैसे करें

याद रखें कि z-स्कोर हमें बस यह बताता है कि एक मान माध्य से कितने मानक विचलन है।

A z स्कोर सकारात्मक, नकारात्मक या शून्य हो सकता है।

एक सकारात्मक z स्कोर इंगित करता है कि एक विशेष मान औसत से ऊपर है, एक नकारात्मक z स्कोर इंगित करता है कि एक विशेष मान औसत से नीचे है, और शून्य का एज़ स्कोर इंगित करता है कि एक विशेष मान औसत के बराबर है।

हमारे उदाहरण में, हमने पाया कि माध्य 14.375 था और मानक विचलन 4.998 था।

तो हमारे डेटासेट में पहला मान 7 था, जिसका z-स्कोर (7-14.375) / 4.998 = -1.47546 था। इसका मतलब है कि मान “7” माध्य से -1.47545 मानक विचलन कम है।

हमारे डेटा में अगला मान, 12, का z-स्कोर (12-14.375) / 4.998 = -0.47515 था। इसका मतलब है कि मान “12” माध्य से -0.47515 मानक विचलन कम है।

कोई मान माध्य से जितना दूर होगा, उस मान के लिए z-स्कोर का निरपेक्ष मान उतना ही अधिक होगा।

उदाहरण के लिए, मान 7, मान 12 की तुलना में माध्य (14.375) से अधिक है, जो बताता है कि 7 में बड़े निरपेक्ष मान के साथ z-स्कोर क्यों था।

अतिरिक्त संसाधन

निम्नलिखित आलेख Excel में z-स्कोर के साथ काम करने के तरीके के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

Excel में Z स्कोर से P मान कैसे ज्ञात करें
Excel में Z स्कोर और प्रतिशतक के बीच कैसे कनवर्ट करें