क्या इंटरक्वेर्टाइल रेंज (आईक्यूआर) आउटलेर्स से प्रभावित है?

आँकड़ों में, हम अक्सर यह जानना चाहते हैं कि किसी वितरण में मूल्य कितने व्यापक रूप से “फैले” हैं।

प्रसार को मापने का एक लोकप्रिय तरीका इंटरक्वर्टाइल रेंज है, जिसकी गणना डेटा सेट के पहले चतुर्थक और तीसरे चतुर्थक के बीच अंतर के रूप में की जाती है। चतुर्थक केवल वे मान हैं जो डेटा सेट को चार बराबर भागों में विभाजित करते हैं।

उदाहरण: अंतरचतुर्थक सीमा की गणना

निम्नलिखित उदाहरण दिखाता है कि किसी दिए गए डेटा सेट के लिए इंटरक्वेर्टाइल रेंज की गणना कैसे करें:

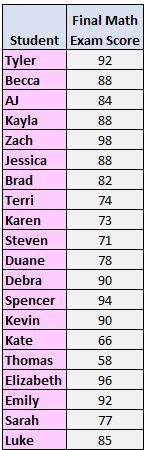
चरण 1: मानों को सबसे छोटे से सबसे बड़े तक व्यवस्थित करें।

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. माध्यिका ज्ञात कीजिए।

58, 66, 71, 73, 74, 77 , 78 , 82 , 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

इस मामले में, माध्यिका 85 और 88 के बीच है।

3. माध्यिका डेटा सेट को दो भागों में विभाजित करती है। निचले आधे का माध्य निचला चतुर्थक है और ऊपरी आधे का माध्य ऊपरी चतुर्थक है:

58, 66, 71, 73 , 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. अंतरचतुर्थक सीमा की गणना करें.

इस मामले में, पहला चतुर्थक डेटा सेट के निचले आधे भाग में मध्य दो मानों का औसत है (75.5) और तीसरा चतुर्थक सेट डेटा के शीर्ष आधे भाग में मध्य दो मानों का औसत है (91).

तो अंतरचतुर्थक सीमा 91 – 75.5 = 15.5 है

इंटरक्वेर्टाइल रेंज आउटलेर्स से प्रभावित नहीं होती है

डेटा सेट के “प्रसार” की गणना करते समय लोगों द्वारा इंटरक्वेर्टाइल रेंज (आईक्यूआर) का उपयोग करना पसंद करने का एक कारण यह है कि यह आउटलेर्स के लिए मजबूत है। चूँकि IQR डेटा मानों की केवल मध्य 50% सीमा है, यह अत्यधिक आउटलेर्स से प्रभावित नहीं होता है।

इसे प्रदर्शित करने के लिए, निम्नलिखित डेटासेट पर विचार करें:

[1, 4, 8, 11, 13, 17, 17, 20]

इस डेटासेट के लिए अलग-अलग प्रसार मेट्रिक्स यहां दिए गए हैं:

• अंतरचतुर्थक सीमा: 11
• रेंज: 19
• मानक विचलन: 6.26
• अंतर: 39.23

अब उसी डेटा सेट पर विचार करें लेकिन एक अत्यधिक बाहरी चीज़ के साथ:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

इस डेटासेट के लिए अलग-अलग प्रसार मेट्रिक्स यहां दिए गए हैं:

• अंतरचतुर्थक सीमा: 12.5
• रेंज: 149
• मानक विचलन: 43.96
• फैलाव: 1,932.84

ध्यान दें कि कैसे अंतरचतुर्थक सीमा 11 से 12.5 तक केवल थोड़ी सी बदलती है। हालाँकि, फैलाव के अन्य सभी उपाय नाटकीय रूप से बदलते हैं।

यह दर्शाता है कि अंतरचतुर्थक सीमा फैलाव के अन्य उपायों की तरह आउटलेर्स से प्रभावित नहीं होती है। इस कारण से, यह किसी भी वितरण में मध्य 50% मूल्यों के वितरण को मापने का एक विश्वसनीय तरीका है।

अग्रिम पठन:

फैलाव माप
इंटरक्वेर्टाइल रेंज कैलकुलेटर