X^2 के अपेक्षित मान की गणना कैसे करें

एक यादृच्छिक चर के लिए, जिसे X दर्शाया गया है, आप X ² के अपेक्षित मान की गणना करने के लिए निम्न सूत्र का उपयोग कर सकते हैं:

ई(एक्स ² ) = Σx ² * पी(एक्स)

सोना:

• Σ : एक प्रतीक जिसका अर्थ है “योग”
• x : यादृच्छिक चर का मान
• p(x) : संभावना है कि यादृच्छिक चर एक दिया गया मान लेता है

निम्नलिखित उदाहरण दिखाता है कि व्यवहार में इस सूत्र का उपयोग कैसे करें।

उदाहरण: एक्स ² के अपेक्षित मूल्य की गणना

मान लीजिए कि हमारे पास निम्नलिखित संभाव्यता वितरण तालिका है जो इस संभावना का वर्णन करती है कि एक यादृच्छिक चर,

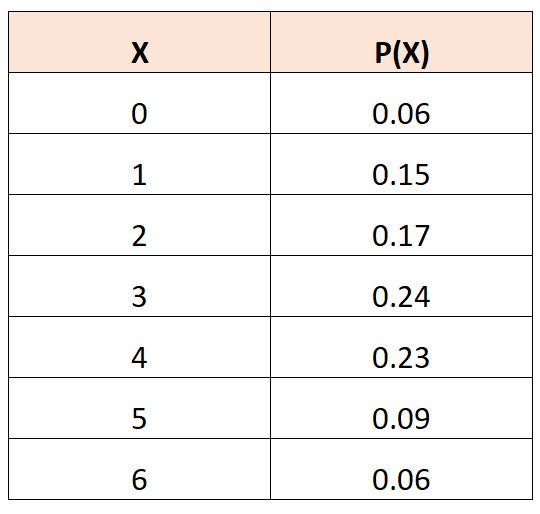
X ² के अपेक्षित मान की गणना करने के लिए, हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

ई(एक्स ² ) = Σx ² * पी(एक्स)

ई(एक्स ² ) = (0) ² *.06 + (1) ² *.15 + (2) ² *.17 + (3) ² *.24 + (4) ² *.23 + (5) ² *.09 + (6) ² *.06

ई(एक्स ² ) = 0 + 0.15 + 0.68 + 2.16 + 3.68 + 2.25+ 2.16

ई( ^{एक्स2} ) = 11.08

X ² का अपेक्षित मान 11.08 है।

ध्यान दें कि यह यादृच्छिक चर एक असतत यादृच्छिक चर है, जिसका अर्थ है कि यह केवल सीमित संख्या में मान ले सकता है।

यदि X एक सतत यादृच्छिक चर है, तो हमें X ² के अपेक्षित मान की गणना करने के लिए निम्नलिखित सूत्र का उपयोग करना चाहिए:

E(X ² ) = ∫ x ² f(x)dx

सोना:

• ∫: एक प्रतीक जिसका अर्थ है “एकीकरण”
• f(x) : यादृच्छिक चर के लिए पीडीएफ जारी है

निरंतर यादृच्छिक चर के लिए ^X2 के अपेक्षित मान की गणना करते समय, हम आमतौर पर सांख्यिकीय सॉफ़्टवेयर का उपयोग करते हैं क्योंकि यह गणना मैन्युअल रूप से करना अधिक कठिन हो सकता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि सांख्यिकी में अन्य सामान्य कार्य कैसे करें:

संभाव्यता वितरण का माध्य कैसे ज्ञात करें
संभाव्यता वितरण का मानक विचलन कैसे ज्ञात करें
संभाव्यता वितरण का प्रसरण कैसे ज्ञात करें