शेष अंतर क्या है? (परिभाषा & #038; उदाहरण)

अवशिष्ट विचरण (कभी-कभी “अस्पष्टीकृत विचरण” कहा जाता है) एक मॉडल में विचरण को संदर्भित करता है जिसे मॉडल चर द्वारा समझाया नहीं जा सकता है।

किसी मॉडल का अवशिष्ट विचरण जितना अधिक होगा, मॉडल डेटा में भिन्नता को समझाने में उतना ही कम सक्षम होगा।

अवशिष्ट भिन्नता दो अलग-अलग सांख्यिकीय मॉडल के परिणामों में प्रकट होती है:

1. एनोवा: तीन या अधिक स्वतंत्र समूहों के साधनों की तुलना करने के लिए उपयोग किया जाता है।

2. प्रतिगमन: एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को मापने के लिए उपयोग किया जाता है।

निम्नलिखित उदाहरण दिखाते हैं कि इनमें से प्रत्येक विधि में अवशिष्ट विचरण की व्याख्या कैसे की जाए।

एनोवा मॉडल में अवशिष्ट विचरण

हर बार जब हम एक एनोवा (“विचरण का विश्लेषण”) मॉडल फिट करते हैं, तो हम एक एनोवा तालिका के साथ समाप्त होते हैं जो निम्नलिखित की तरह दिखती है:

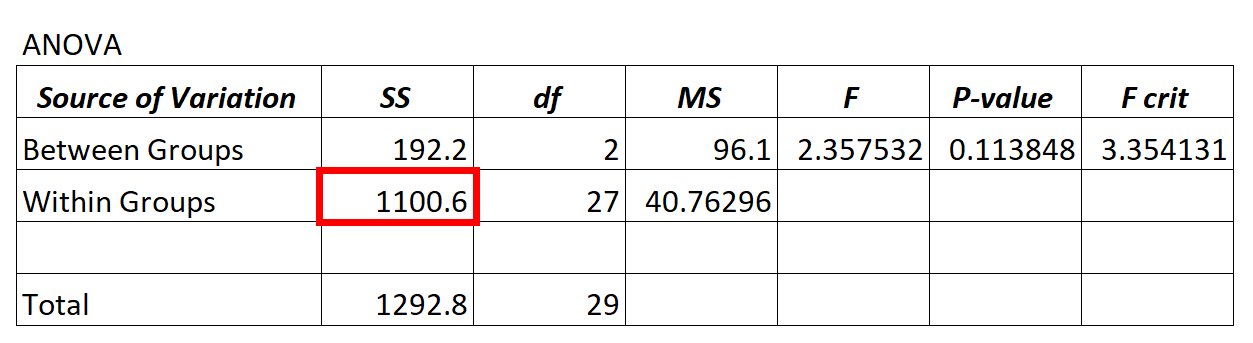
एनोवा मॉडल से अवशिष्ट विचरण मान समूह के भीतर भिन्नता के लिए एसएस (“वर्गों का योग”) कॉलम में पाया जाता है।

इस मान को “वर्ग त्रुटियों का योग” भी कहा जाता है और इसकी गणना निम्न सूत्र का उपयोग करके की जाती है:

Σ(एक्स _आईजे – एक्स _जे ) ²

सोना:

• Σ : एक ग्रीक प्रतीक जिसका अर्थ है “योग”
• X _ij : समूह j का ^ith अवलोकन
• X _j : समूह j का औसत

उपरोक्त एनोवा मॉडल में, हम देखते हैं कि अवशिष्ट विचरण 1100.6 है।

यह निर्धारित करने के लिए कि क्या यह अवशिष्ट विचरण “उच्च” है, हम समूहों के भीतर वर्गों के औसत योग और समूहों के बीच वर्गों के औसत योग की गणना कर सकते हैं और दोनों के बीच का अनुपात ढूंढ सकते हैं, जो एनोवा तालिका में समग्र एफ मान देता है।

• एफ = एमएस _{प्रवेश करता है} / एमएस _{प्रवेश करता है}
• एफ = 96.1/40.76296
• एफ = 2.357

उपरोक्त एनोवा तालिका में एफ मान 2.357 है और संबंधित पी मान 0.113848 है। चूँकि यह p-मान α = 0.05 से कम नहीं है, हमारे पास शून्य परिकल्पना को अस्वीकार करने के लिए पर्याप्त सबूत नहीं हैं।

इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि जिन समूहों की हम तुलना कर रहे हैं उनके बीच औसत अंतर काफी भिन्न है।

यह हमें बताता है कि एनोवा मॉडल का अवशिष्ट विचरण उस भिन्नता की तुलना में अधिक है जिसे मॉडल वास्तव में समझा सकता है।

प्रतिगमन मॉडल में अवशिष्ट विचरण

एक प्रतिगमन मॉडल में, अवशिष्ट विचरण को अनुमानित डेटा बिंदुओं और देखे गए डेटा बिंदुओं के बीच अंतर के वर्गों के योग के रूप में परिभाषित किया गया है।

इसकी गणना इस प्रकार की जाती है:

Σ(ŷ _i – y _i ) ²

सोना:

• Σ : एक ग्रीक प्रतीक जिसका अर्थ है “योग”
• ŷ _i : अनुमानित डेटा बिंदु
• y _i : प्रेक्षित डेटा बिंदु

जब हम एक प्रतिगमन मॉडल फिट करते हैं, तो हमें आमतौर पर एक परिणाम मिलता है जो निम्नलिखित जैसा दिखता है:

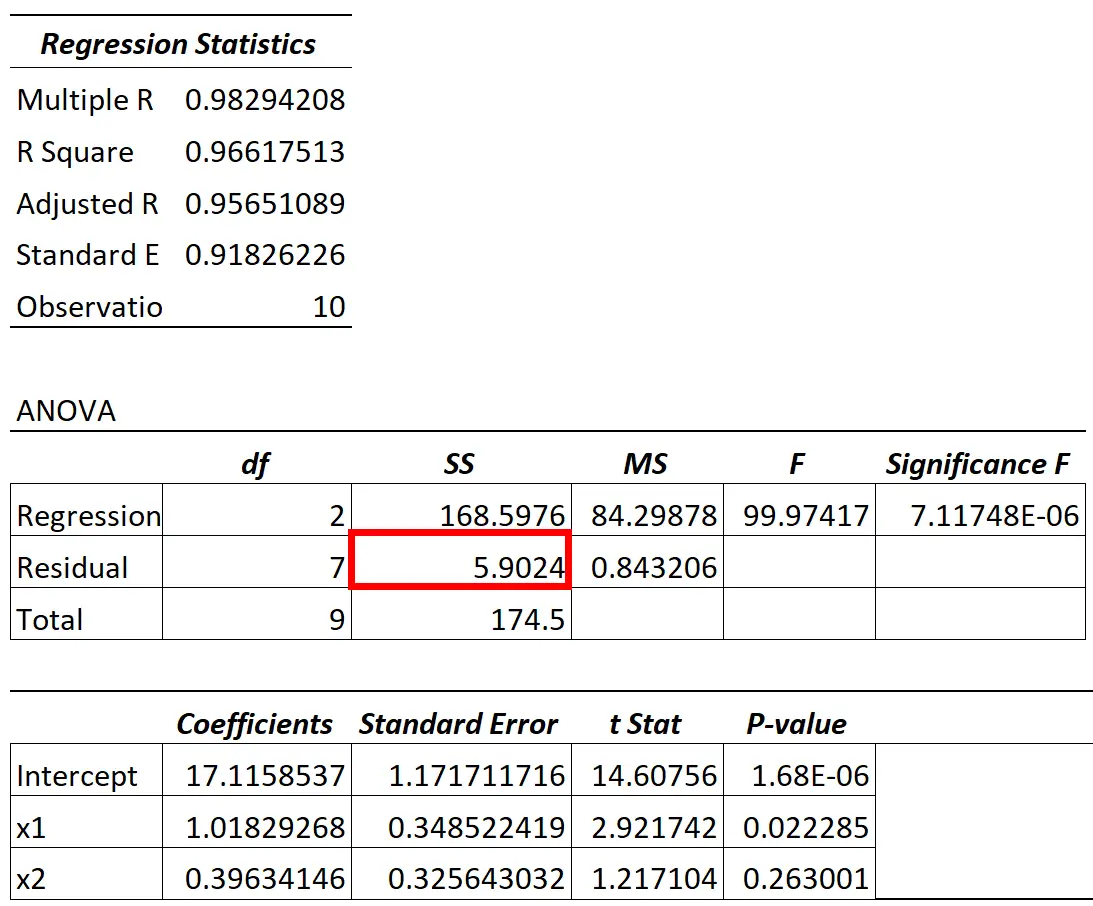
एनोवा मॉडल से अवशिष्ट विचरण मान अवशिष्ट भिन्नता के लिए एसएस (“वर्गों का योग”) कॉलम में पाया जा सकता है।

मॉडल में कुल भिन्नता के लिए अवशिष्ट भिन्नता का अनुपात हमें प्रतिक्रिया चर में भिन्नता का प्रतिशत बताता है जिसे मॉडल में भविष्यवक्ता चर द्वारा समझाया नहीं जा सकता है।

उदाहरण के लिए, उपरोक्त तालिका में, हम इस प्रतिशत की गणना इस प्रकार करेंगे:

• अस्पष्टीकृत भिन्नता = एसएस अवशिष्ट / एसएस कुल
• अस्पष्टीकृत भिन्नता = 5.9024 / 174.5
• अस्पष्टीकृत भिन्नता = 0.0338

इस मान की गणना निम्न सूत्र का उपयोग करके भी की जा सकती है:

• अस्पष्टीकृत भिन्नता = 1 – आर ²
• अस्पष्टीकृत भिन्नता = 1 – 0.96617
• अस्पष्टीकृत भिन्नता = 0.0338

मॉडल का आर-वर्ग मान हमें प्रतिक्रिया चर में भिन्नता का प्रतिशत बताता है जिसे भविष्यवक्ता चर द्वारा समझाया जा सकता है।

इस प्रकार, अस्पष्टीकृत भिन्नता जितनी कम होगी, एक मॉडल प्रतिक्रिया चर में भिन्नता को समझाने के लिए भविष्यवक्ता चर का उपयोग करने में उतना ही अधिक सक्षम होगा।

अतिरिक्त संसाधन

एक अच्छा आर-वर्ग मान क्या है?
एक्सेल में आर-स्क्वायर की गणना कैसे करें
आर में आर-वर्ग की गणना कैसे करें