सांख्यिकी में अवशेष क्या हैं?

अवशिष्ट प्रतिगमन विश्लेषण में देखे गए मूल्य और अनुमानित मूल्य के बीच का अंतर है।

इसकी गणना इस प्रकार की जाती है:

अवशिष्ट = प्रेक्षित मूल्य – अनुमानित मूल्य

याद रखें कि रैखिक प्रतिगमन का लक्ष्य एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को मापना है। ऐसा करने के लिए, रैखिक प्रतिगमन उस रेखा को ढूंढता है जो डेटा को सबसे अच्छी तरह से “फिट” करती है, जिसे कम से कम वर्ग प्रतिगमन रेखा कहा जाता है।

यह रेखा डेटा सेट में प्रत्येक अवलोकन के लिए एक भविष्यवाणी उत्पन्न करती है, लेकिन यह संभावना नहीं है कि प्रतिगमन रेखा द्वारा की गई भविष्यवाणी बिल्कुल देखे गए मूल्य से मेल खाएगी।

पूर्वानुमान और देखे गए मूल्य के बीच का अंतर अवशिष्ट है। यदि हम देखे गए मानों को प्लॉट करते हैं और फिटेड रिग्रेशन लाइन को सुपरइम्पोज़ करते हैं, तो प्रत्येक अवलोकन के लिए अवशेष अवलोकन और रिग्रेशन लाइन के बीच ऊर्ध्वाधर दूरी होगी:

एक अवलोकन में एक सकारात्मक अवशिष्ट होता है यदि इसका मूल्य प्रतिगमन रेखा द्वारा बनाए गए अनुमानित मूल्य से अधिक है।

इसके विपरीत, यदि किसी अवलोकन का मान प्रतिगमन रेखा द्वारा बनाए गए पूर्वानुमानित मान से कम है, तो उसका अवशिष्ट नकारात्मक होता है।

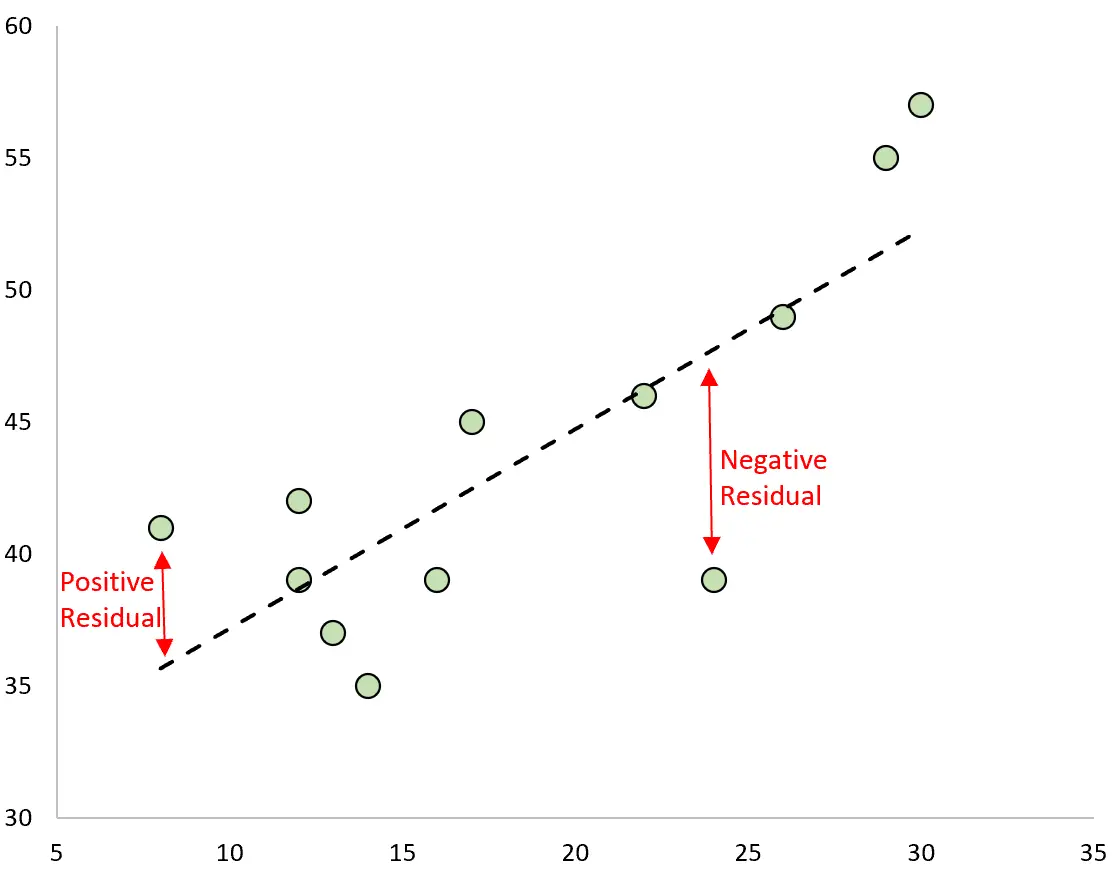
कुछ अवलोकनों में सकारात्मक अवशेष होंगे जबकि अन्य में नकारात्मक अवशेष होंगे, लेकिन सभी अवशेषों का योग शून्य होगा।

अवशेषों की गणना का उदाहरण

मान लीजिए कि हमारे पास कुल 12 अवलोकनों के साथ निम्नलिखित डेटासेट हैं:

यदि हम इस डेटा सेट में एक रेखीय प्रतिगमन रेखा को फिट करने के लिए सांख्यिकीय सॉफ़्टवेयर (जैसे आर , एक्सेल , पायथन , स्टाटा , आदि) का उपयोग करते हैं, तो हम पाएंगे कि सबसे अच्छी-फिट लाइन यह होगी:

y = 29.63 + 0.7553x

इस पंक्ति का उपयोग करके, हम X के मान के आधार पर प्रत्येक Y मान के लिए अनुमानित मान की गणना कर सकते हैं। उदाहरण के लिए, पहले अवलोकन का अनुमानित मान होगा:

y = 29.63 + 0.7553*(8) = 35.67

फिर हम इस अवलोकन के लिए शेष की गणना इस प्रकार कर सकते हैं:

अवशिष्ट = प्रेक्षित मूल्य – अनुमानित मूल्य = 41 – 35.67 = 5.33

हम प्रत्येक अवलोकन के लिए अवशेष खोजने के लिए इस प्रक्रिया को दोहरा सकते हैं:

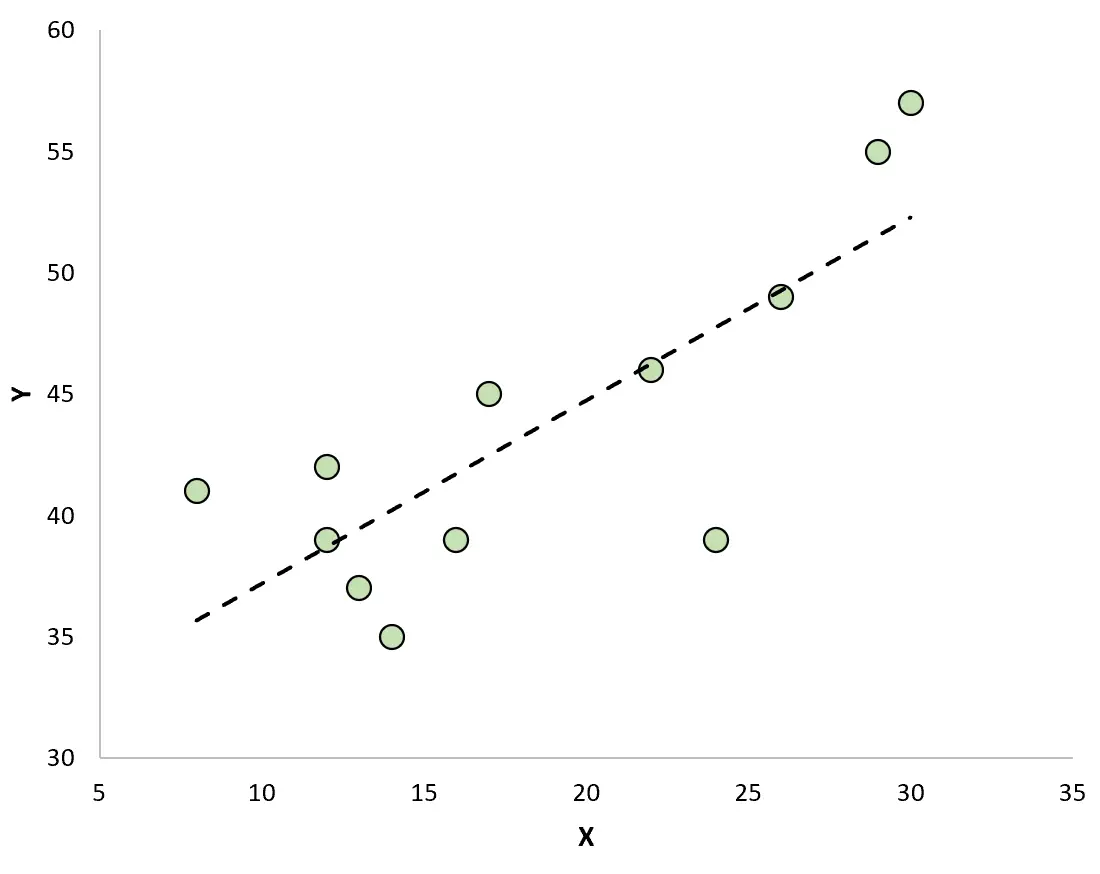
यदि हम फिट प्रतिगमन रेखा के साथ अवलोकनों को देखने के लिए एक स्कैटरप्लॉट बनाते हैं, तो हम देखेंगे कि कुछ अवलोकन रेखा के ऊपर हैं जबकि अन्य रेखा के नीचे हैं:

अवशेषों के गुण

अवशेषों में निम्नलिखित गुण होते हैं:

• डेटा सेट में प्रत्येक अवलोकन में एक संगत अवशेष होता है। इसलिए, यदि किसी डेटासेट में कुल 100 अवलोकन हैं, तो मॉडल 100 अनुमानित मान उत्पन्न करेगा, जिसके परिणामस्वरूप कुल 100 अवशेष होंगे।
• सभी अवशेषों का योग शून्य है।
• अवशेषों का औसत मान शून्य है.

व्यवहार में अवशेषों का उपयोग कैसे किया जाता है?

व्यवहार में, प्रतिगमन में अवशेषों का उपयोग तीन अलग-अलग कारणों से किया जाता है:

1. मॉडल की पर्याप्तता का मूल्यांकन करें.

एक बार जब हम एक फिट प्रतिगमन रेखा तैयार कर लेते हैं, तो हम वर्गों के अवशिष्ट योग (आरएसएस) की गणना कर सकते हैं, जो सभी वर्ग अवशेषों का योग है। आरएसएस जितना कम होगा, प्रतिगमन मॉडल डेटा में उतना ही बेहतर फिट होगा।

2. सामान्यता धारणा की जाँच करें।

रैखिक प्रतिगमन की प्रमुख धारणाओं में से एक यह है कि अवशेष सामान्य रूप से वितरित होते हैं।

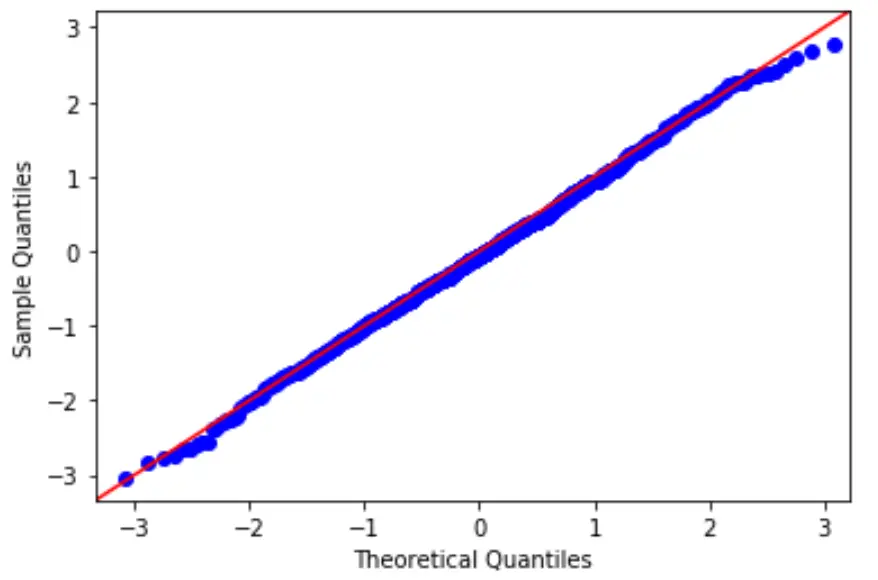
इस परिकल्पना का परीक्षण करने के लिए, हम एक QQ प्लॉट बना सकते हैं, जो एक प्रकार का प्लॉट है जिसका उपयोग हम यह निर्धारित करने के लिए कर सकते हैं कि किसी मॉडल के अवशेष सामान्य वितरण का पालन करते हैं या नहीं।

यदि प्लॉट पर बिंदु मोटे तौर पर एक सीधी विकर्ण रेखा बनाते हैं, तो सामान्यता की धारणा पूरी होती है।

3. समरूपता धारणा की जाँच करें।

रैखिक प्रतिगमन की एक अन्य प्रमुख धारणा यह है कि x के प्रत्येक स्तर पर अवशेषों में निरंतर भिन्नता होती है। इसे होमोसेडैस्टिसिटी कहा जाता है। जब ऐसा नहीं होता है, तो अवशेष विषमलैंगिकता से पीड़ित होते हैं।

यह जांचने के लिए कि क्या यह धारणा पूरी हुई है, हम एक अवशिष्ट प्लॉट बना सकते हैं, जो एक स्कैटरप्लॉट है जो मॉडल के अनुमानित मूल्यों के विरुद्ध अवशिष्ट दिखाता है।

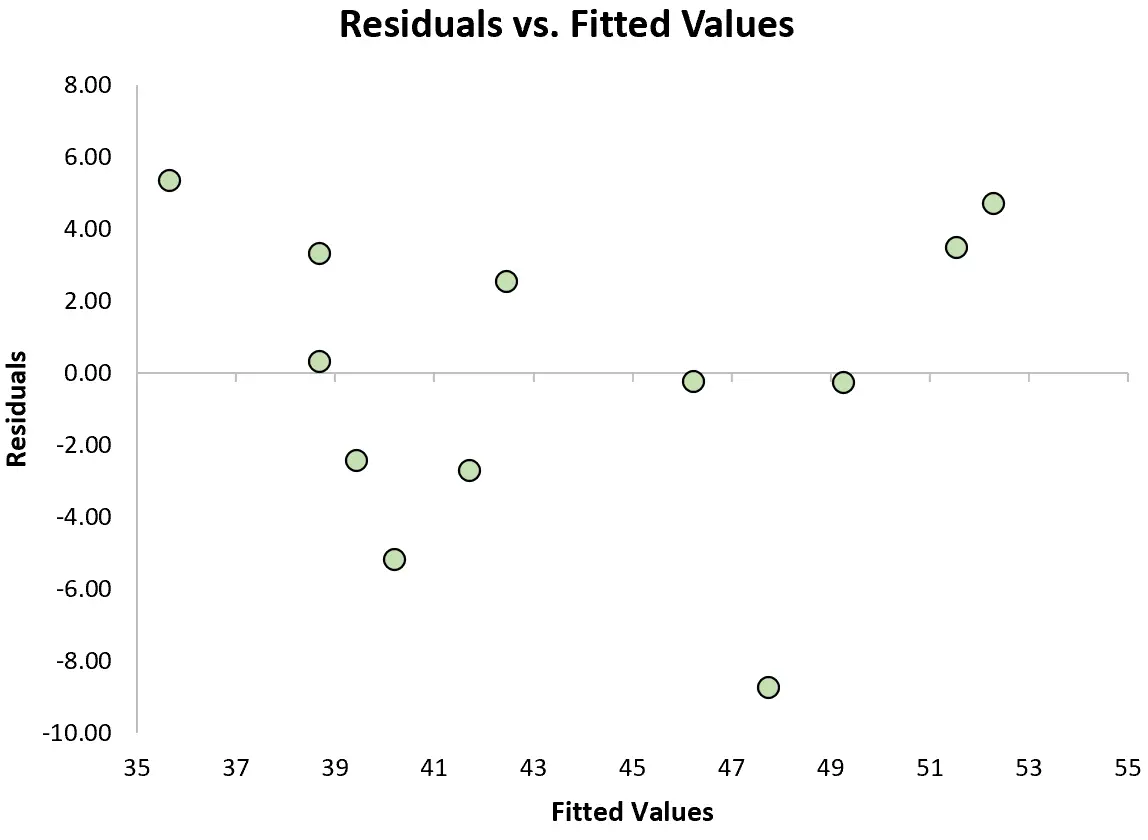
यदि ग्राफ़ में अवशेषों को बिना किसी स्पष्ट प्रवृत्ति के लगभग शून्य के आसपास समान रूप से वितरित किया जाता है, तो हम आम तौर पर कहते हैं कि समरूपता की धारणा पूरी हो गई है।

अतिरिक्त संसाधन

सरल रेखीय प्रतिगमन का परिचय
एकाधिक रेखीय प्रतिगमन का परिचय
रैखिक प्रतिगमन की चार धारणाएँ
एक्सेल में एक अवशिष्ट प्लॉट कैसे बनाएं