एक्सेल में आंशिक एफ टेस्ट कैसे करें

आंशिक एफ-परीक्षण का उपयोग यह निर्धारित करने के लिए किया जाता है कि प्रतिगमन मॉडल और उसी मॉडल के नेस्टेड संस्करण के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं।

एक नेस्टेड मॉडल बस एक मॉडल है जिसमें समग्र प्रतिगमन मॉडल में भविष्यवक्ता चर का एक सबसेट शामिल होता है।

उदाहरण के लिए, मान लें कि हमारे पास चार भविष्यवक्ता चर के साथ निम्नलिखित प्रतिगमन मॉडल है:

वाई = β ₀ + β ₁ x ₁ + β ₂ x ₂ + β ₃ x ₃ + β ₄ x ₄ + ε

नेस्टेड मॉडल का एक उदाहरण निम्नलिखित मॉडल होगा जिसमें केवल दो मूल भविष्यवक्ता चर होंगे:

वाई = β ₀ + β ₁ x ₁ + β ₂ x ₂ + ε

यह निर्धारित करने के लिए कि क्या ये दोनों मॉडल महत्वपूर्ण रूप से भिन्न हैं, हम आंशिक एफ-परीक्षण कर सकते हैं, जो निम्नलिखित एफ-परीक्षण आंकड़ों की गणना करता है:

एफ = (( _कम आरएसएस – _{पूर्ण} आरएसएस)/पी) / ( _{पूर्ण} आरएसएस/एनके)

सोना:

• _कम आरएसएस : कम किए गए (यानी “नेस्टेड”) मॉडल के वर्गों का अवशिष्ट योग।
• RSS _{पूर्ण} : पूर्ण मॉडल के वर्गों का अवशिष्ट योग।
• पी: पूर्ण मॉडल से हटाए गए भविष्यवक्ताओं की संख्या।
• n: डेटासेट में अवलोकनों की कुल संख्या।
• k: पूर्ण मॉडल में गुणांकों की संख्या (इंटरसेप्ट सहित)।

यह परीक्षण निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:

एच ₀ : पूर्ण मॉडल से हटाए गए सभी गुणांक शून्य हैं।

एच _ए : संपूर्ण मॉडल से हटाए गए गुणांकों में से कम से कम एक गैर-शून्य है।

यदि एफ-परीक्षण आंकड़ों के अनुरूप पी-मान एक निश्चित स्तर के महत्व (जैसे 0.05) से नीचे है, तो हम शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि पूर्ण मॉडल से हटाए गए गुणांकों में से कम से कम एक महत्वपूर्ण है।

निम्नलिखित उदाहरण दिखाता है कि एक्सेल में आंशिक एफ परीक्षण कैसे करें।

उदाहरण: एक्सेल में आंशिक एफ परीक्षण

मान लीजिए हमारे पास एक्सेल में निम्नलिखित डेटा सेट है:

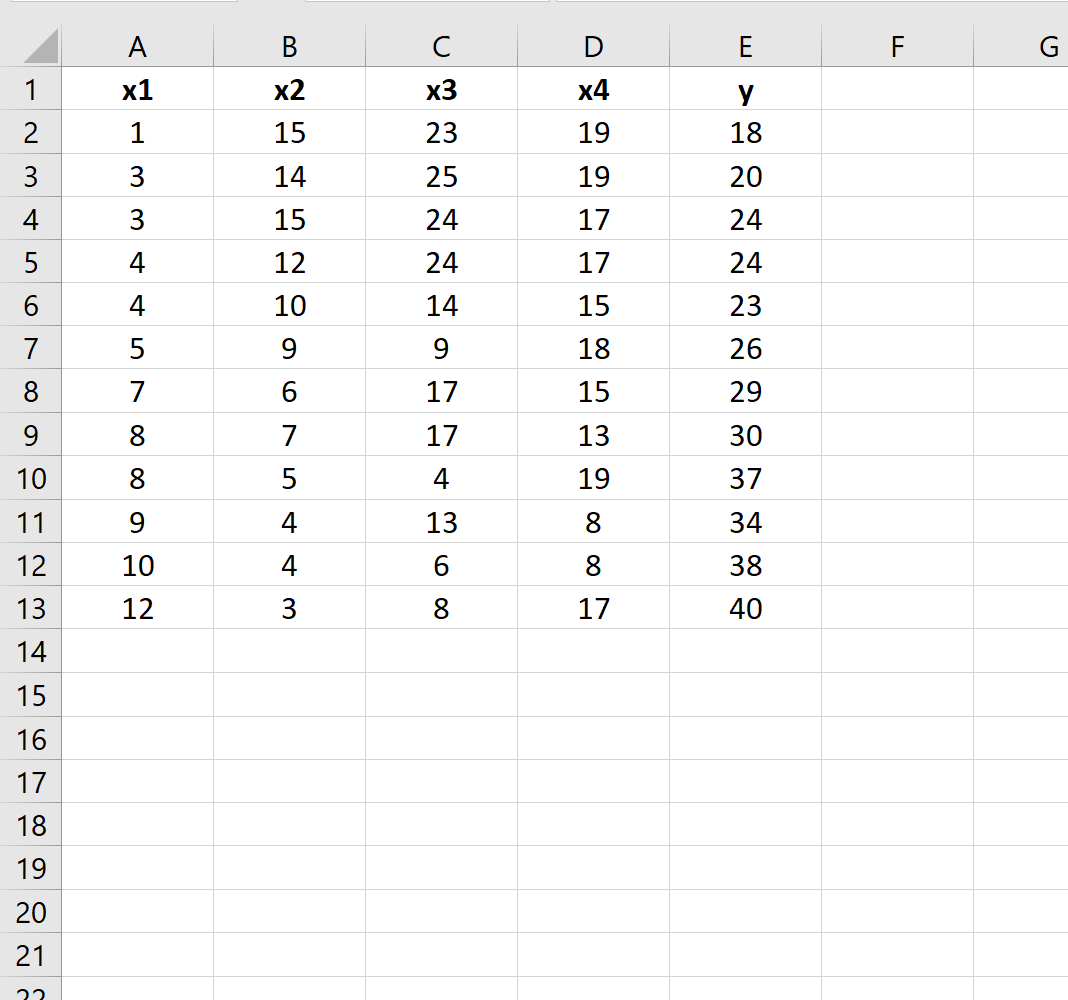
मान लीजिए कि हम यह निर्धारित करना चाहते हैं कि निम्नलिखित दो प्रतिगमन मॉडल के बीच कोई अंतर है या नहीं:

पूर्ण मॉडल: y = β ₀ + β ₁ x ₁ + β ₂ x ₂ + β ₃ x ₃ + β ₄ x ₄

छोटा मॉडल: y = β ₀ + β ₁ x ₁ + β ₂ x ₂

हम निम्नलिखित परिणाम प्राप्त करने के लिए प्रत्येक मॉडल के लिए एक्सेल में एकाधिक रैखिक प्रतिगमन कर सकते हैं:

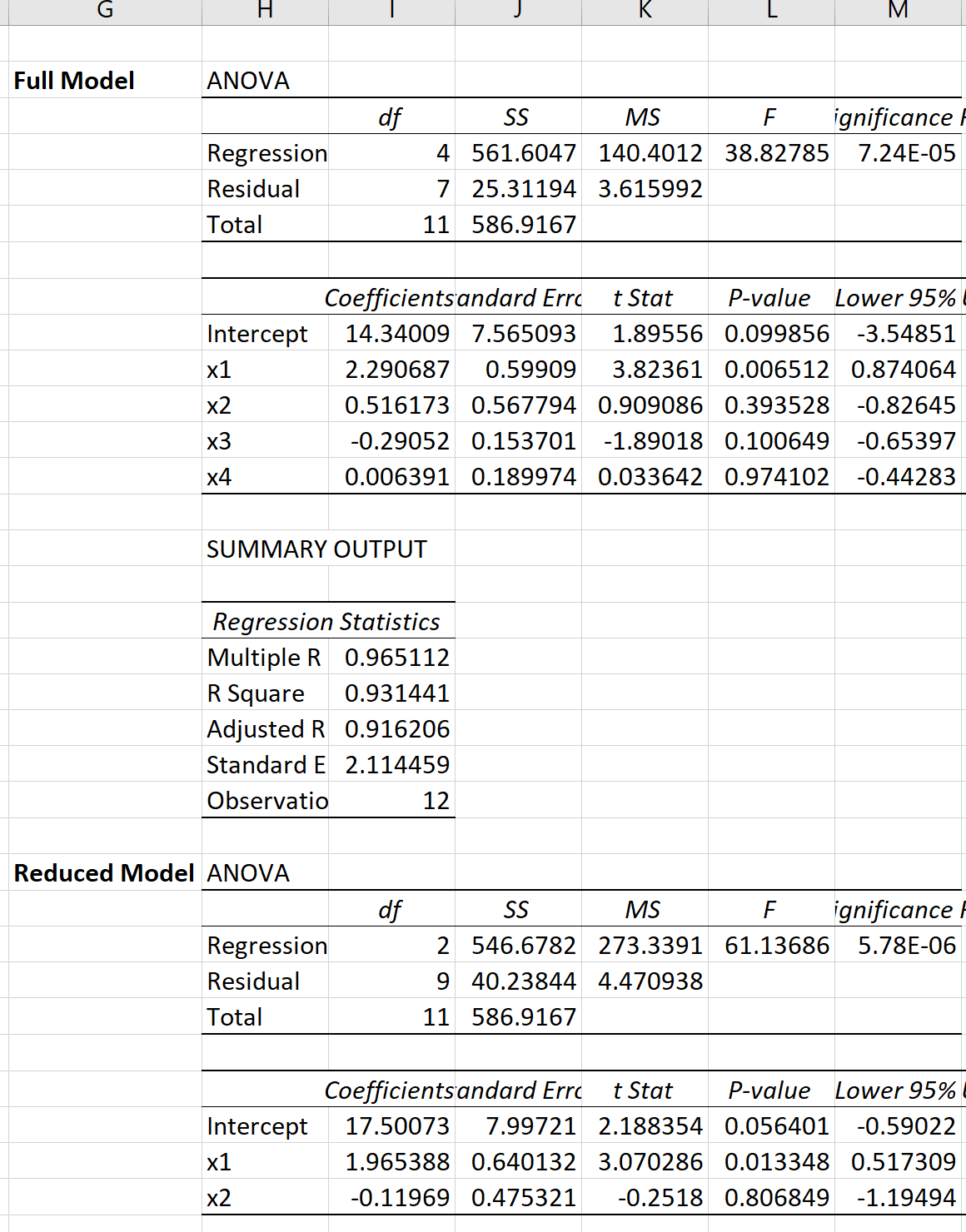
फिर हम आंशिक एफ-परीक्षण के लिए एफ-परीक्षण आंकड़ों की गणना करने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं:

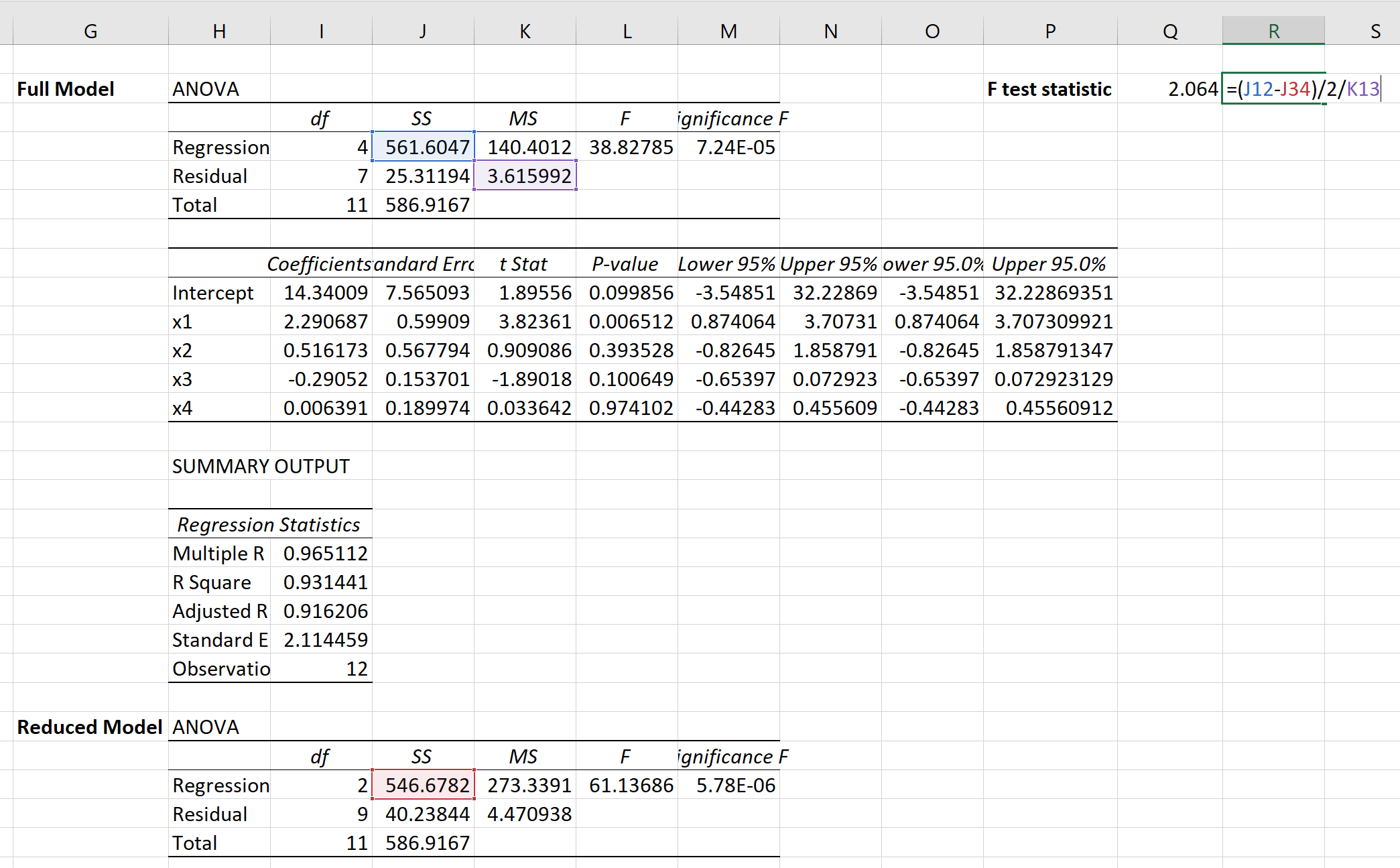
परीक्षण आँकड़ा 2.064 निकला।

फिर हम संबंधित पी-वैल्यू की गणना करने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं:

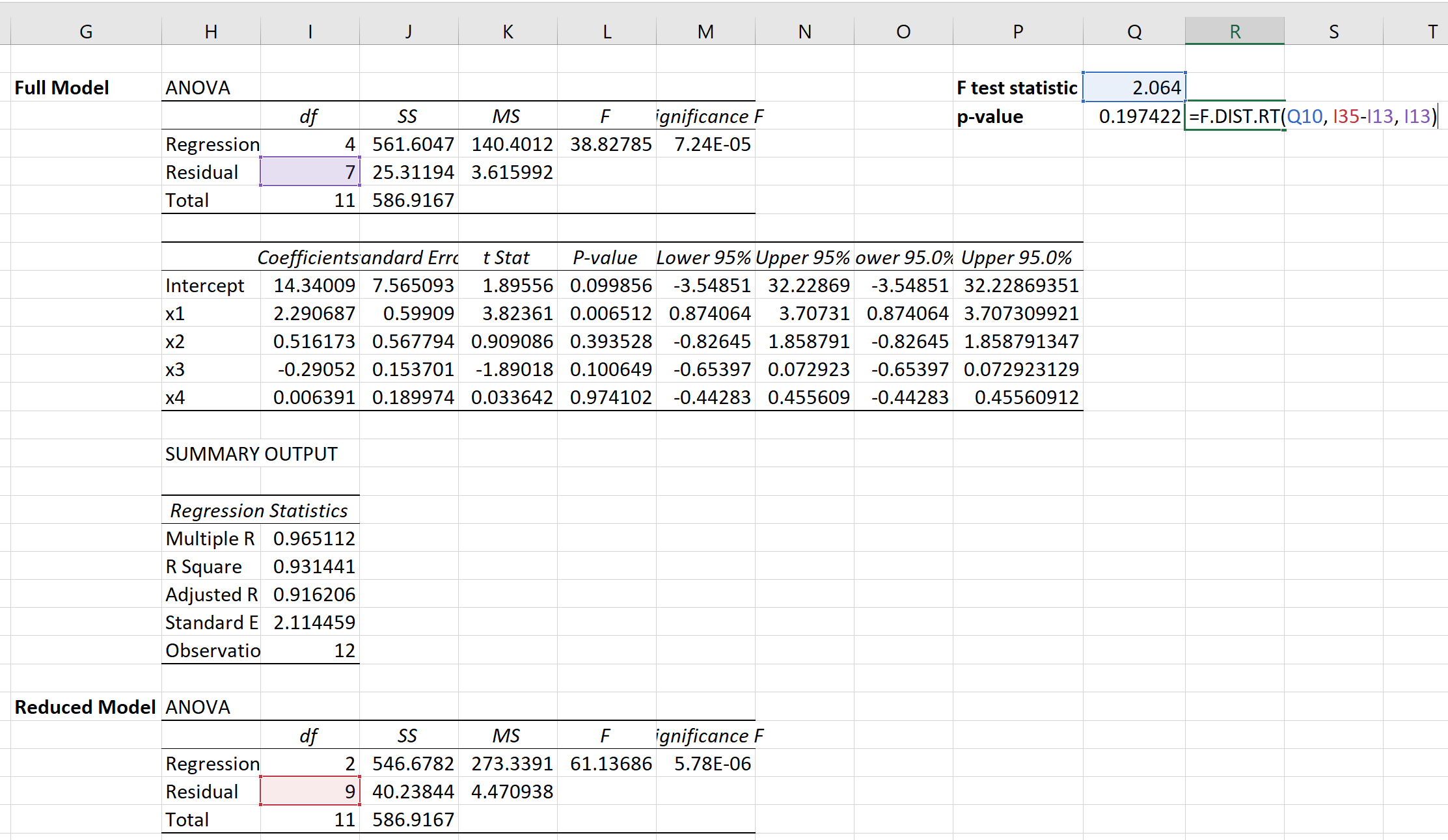
पी-वैल्यू 0.1974 निकला।

चूँकि यह पी-मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहेंगे। इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि x3 या x4 भविष्यवक्ता चर में से कोई भी सांख्यिकीय रूप से महत्वपूर्ण है।

दूसरे शब्दों में, प्रतिगमन मॉडल में x3 और x4 जोड़ने से मॉडल फिट में उल्लेखनीय सुधार नहीं होता है।

अतिरिक्त संसाधन

एक्सेल में सरल रैखिक प्रतिगमन कैसे करें
एक्सेल में मल्टीपल लीनियर रिग्रेशन कैसे करें
एक्सेल में रिग्रेशन की मानक त्रुटि की गणना कैसे करें