एक्सेल में आंशिक सहसंबंध की गणना कैसे करें

आंकड़ों में, हम अक्सर दो चरों के बीच रैखिक संबंध को मापने के लिए पियर्सन सहसंबंध गुणांक का उपयोग करते हैं। हालाँकि, कभी-कभी हम तीसरे वेरिएबल को नियंत्रित करते समय दो वेरिएबल्स के बीच संबंध को समझना चाहते हैं।

उदाहरण के लिए, मान लीजिए कि हम कक्षा में छात्र के वर्तमान ग्रेड को नियंत्रित करते हुए, एक छात्र के अध्ययन के घंटों की संख्या और अंतिम परीक्षा ग्रेड के बीच संबंध को मापना चाहते हैं। इस मामले में, हम अध्ययन किए गए घंटों और अंतिम परीक्षा ग्रेड के बीच संबंध को मापने के लिए आंशिक सहसंबंध का उपयोग कर सकते हैं।

यह ट्यूटोरियल बताता है कि एक्सेल में आंशिक सहसंबंध की गणना कैसे करें।

उदाहरण: एक्सेल में आंशिक सहसंबंध

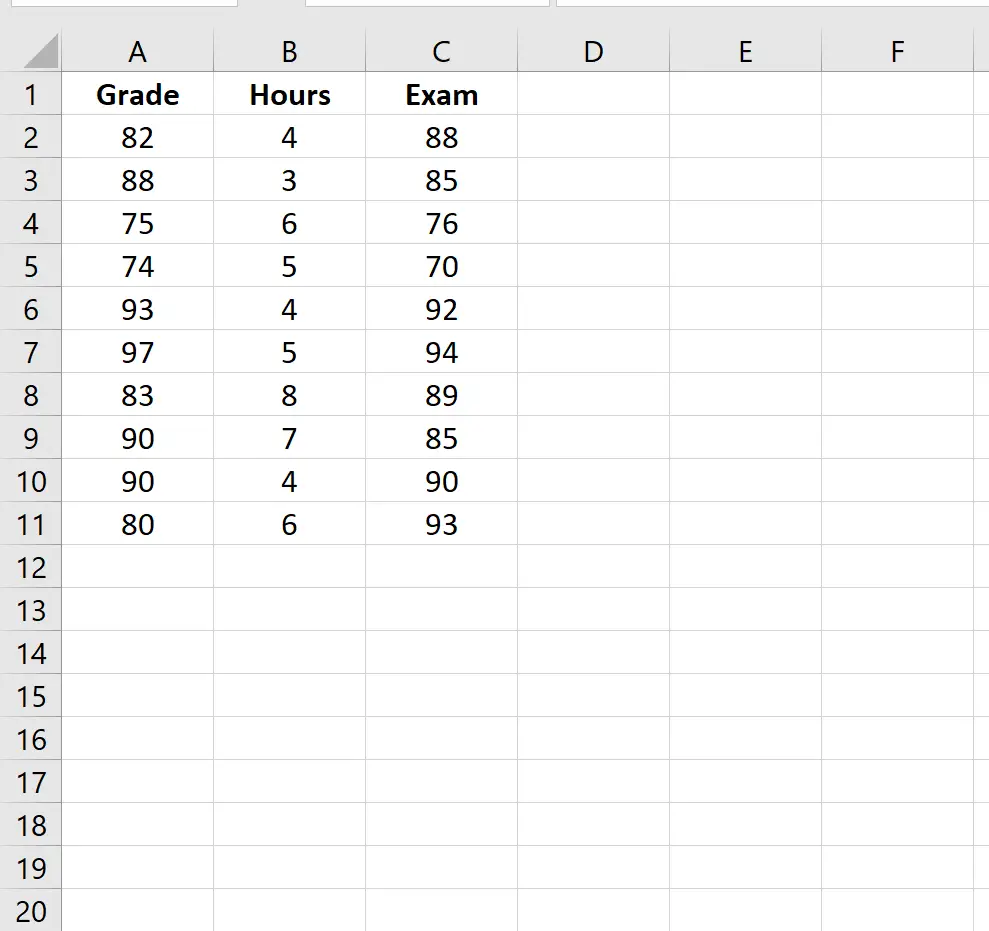
मान लीजिए कि हमारे पास एक डेटासेट है जो 10 छात्रों के लिए निम्नलिखित जानकारी प्रदर्शित करता है:

• किसी कक्षा में वर्तमान ग्रेड
• अंतिम परीक्षा के लिए अध्ययन में घंटों बिताए
• अंतिम परीक्षा स्कोर

वर्तमान ग्रेड को नियंत्रित करते समय अध्ययन किए गए घंटों और परीक्षा ग्रेड के बीच आंशिक सहसंबंध खोजने के लिए निम्नलिखित चरणों का उपयोग करें।

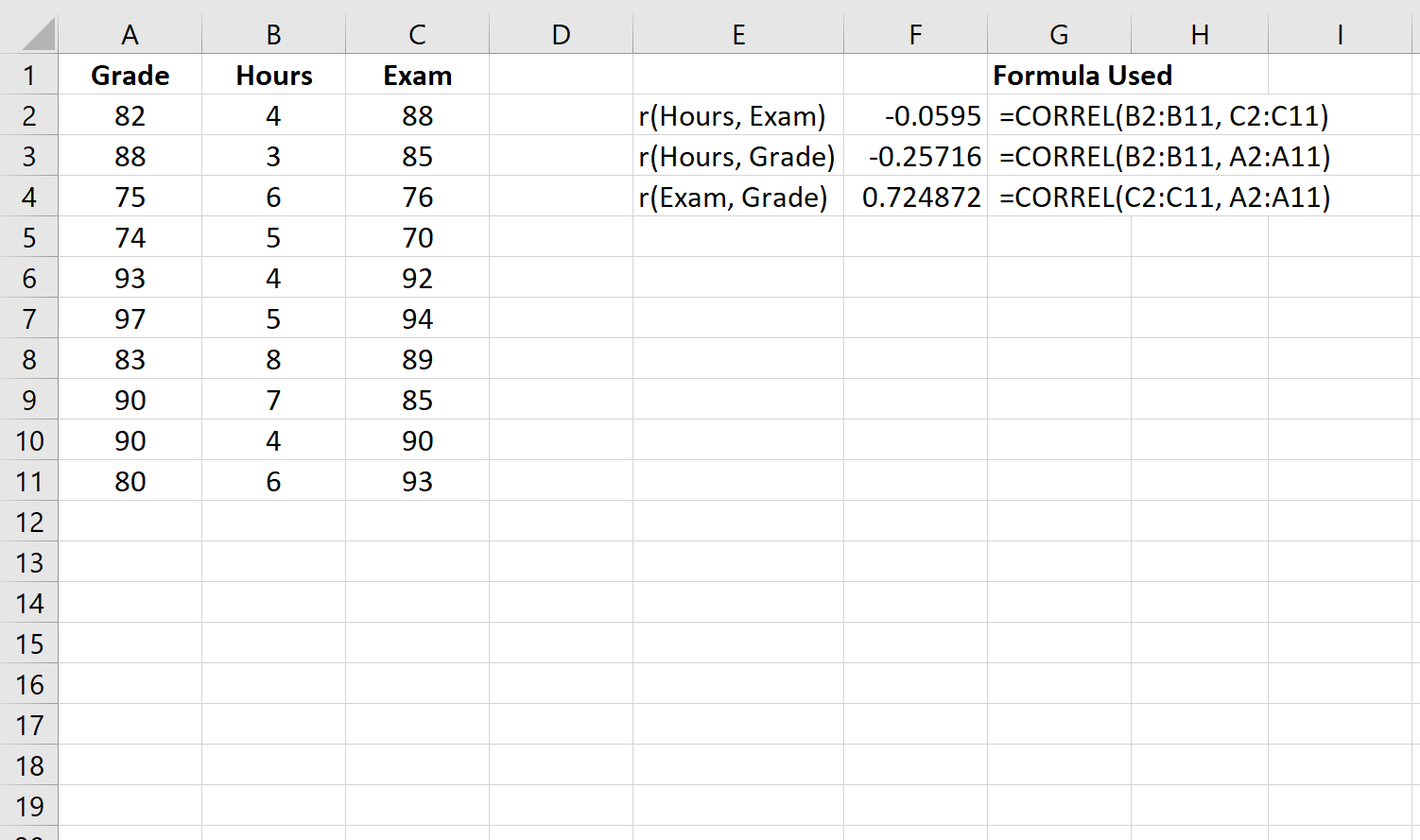
चरण 1: प्रत्येक जोड़ीवार सहसंबंध की गणना करें।

सबसे पहले, हम चरों के प्रत्येक जोड़ीवार संयोजन के बीच सहसंबंध की गणना करेंगे:

चरण 2: घंटों और परीक्षा स्कोर के बीच आंशिक सहसंबंध की गणना करें।

वेरिएबल सी को नियंत्रित करते समय वेरिएबल ए और वेरिएबल बी के बीच आंशिक सहसंबंध की गणना करने का सूत्र इस प्रकार है:

आंशिक सहसंबंध = (आर _ए,बी – आर _ए,सी *आर _{बी,सी} ) / √((1-आर ² _ए,बी )(1-आर ² _{बी,सी} ))

निम्नलिखित स्क्रीनशॉट दिखाता है कि वर्तमान ग्रेड को नियंत्रित करते हुए, घंटों और परीक्षा ग्रेड के बीच आंशिक सहसंबंध की गणना करने के लिए इस सूत्र का उपयोग कैसे करें:

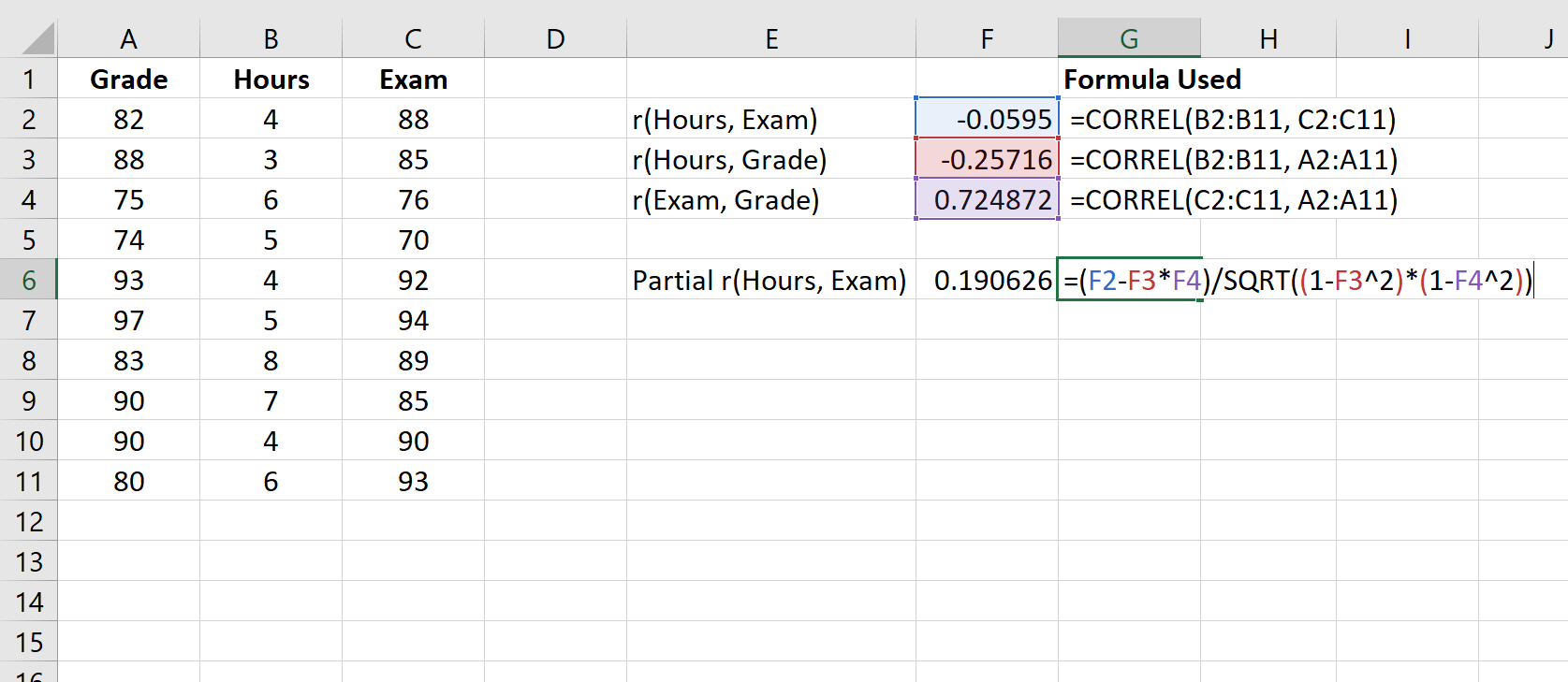
आंशिक सहसंबंध 0.190626 है। यह निर्धारित करने के लिए कि क्या यह सहसंबंध सांख्यिकीय रूप से महत्वपूर्ण है, हम संबंधित पी-मान पा सकते हैं।

चरण 3: आंशिक सहसंबंध के पी-मान की गणना करें।

टी- परीक्षण आँकड़े की गणना निम्नानुसार की जा सकती है:

t = r√(n-3) / √(1-r ² )

निम्नलिखित स्क्रीनशॉट दिखाता है कि परीक्षण आँकड़े और संबंधित पी-वैल्यू की गणना करने के लिए इस सूत्र का उपयोग कैसे करें:

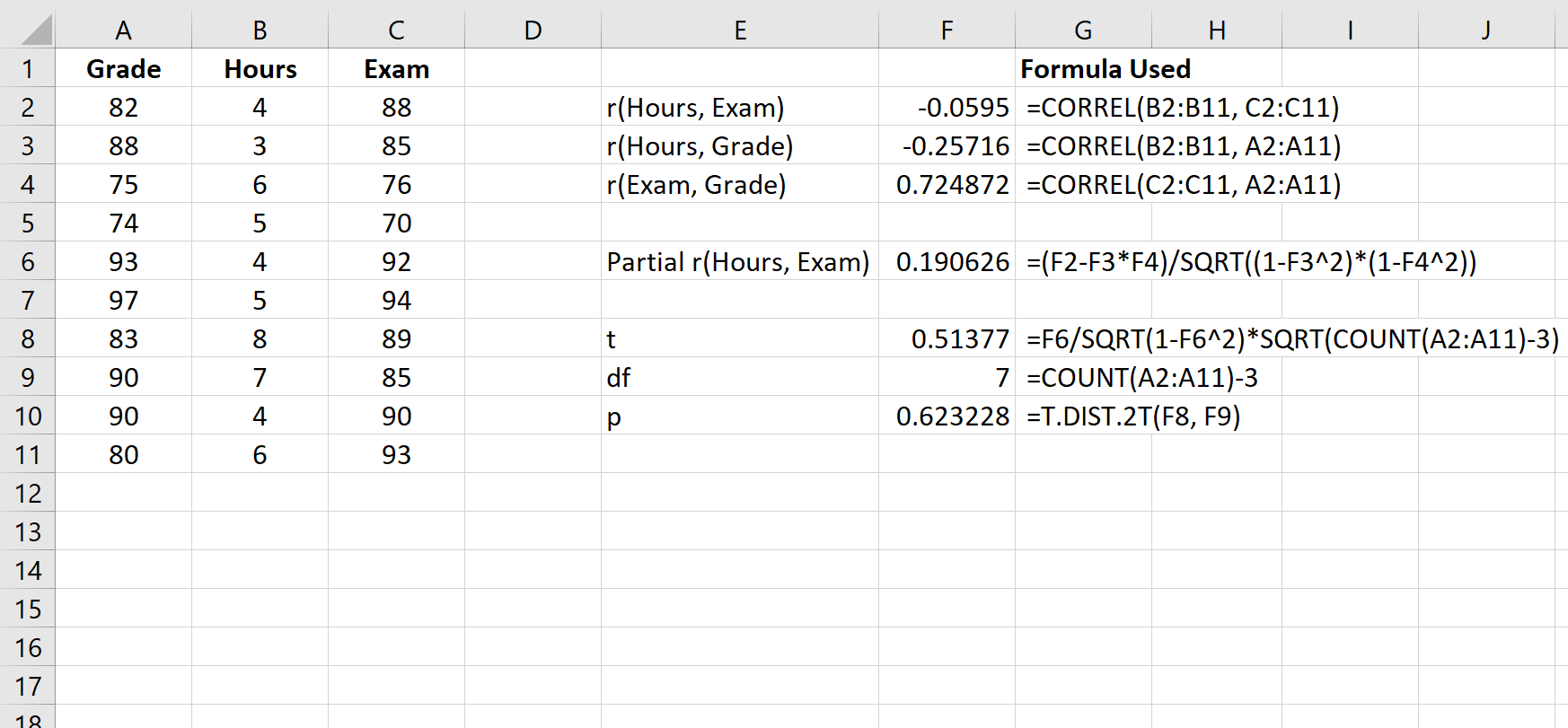
टी- परीक्षण आँकड़ा 0.51377 है। स्वतंत्रता की कोटि की कुल संख्या n-3 = 10-3 = 7 है। संगत पी-मान 0.623228 है। चूँकि यह मान 0.05 से कम नहीं है, इसका मतलब है कि घंटों और परीक्षा परिणामों के बीच आंशिक संबंध सांख्यिकीय रूप से महत्वपूर्ण नहीं है।