एक्सेल में कॉन्फिडेंस इंटरवल की गणना कैसे करें

यह सूत्र निचली सीमा और ऊपरी सीमा के साथ एक अंतराल बनाता है, जिसमें संभवतः कुछ स्तर के आत्मविश्वास के साथ जनसंख्या पैरामीटर शामिल होता है:

आत्मविश्वास अंतराल = [निचली सीमा, ऊपरी सीमा]

यह ट्यूटोरियल बताता है कि एक्सेल में निम्नलिखित कॉन्फिडेंस अंतराल की गणना कैसे करें:

1. माध्य के लिए विश्वास अंतराल

2. साधनों में अंतर के लिए विश्वास अंतराल

3. किसी अनुपात के लिए विश्वास अंतराल

4. अनुपात में अंतर के लिए कॉन्फिडेंस अंतराल

चल दर!

उदाहरण 1: माध्य के लिए विश्वास अंतराल

किसी माध्य के लिए विश्वास अंतराल की गणना करने के लिए हम निम्नलिखित सूत्र का उपयोग करते हैं:

आत्मविश्वास अंतराल = x +/- z*(s/√n)

सोना:

• x : नमूना माध्य
• z: चुना हुआ z मान
• एस: नमूना मानक विचलन
• n: नमूना आकार

उदाहरण: मान लीजिए कि हम निम्नलिखित जानकारी के साथ कछुओं का एक यादृच्छिक नमूना एकत्र करते हैं:

• नमूना आकार n = 25
• औसत नमूना वजन x = 300
• नमूना मानक विचलन s = 18.5

निम्नलिखित स्क्रीनशॉट दिखाता है कि कछुओं की आबादी के वास्तविक औसत वजन के लिए 95% विश्वास अंतराल की गणना कैसे करें:

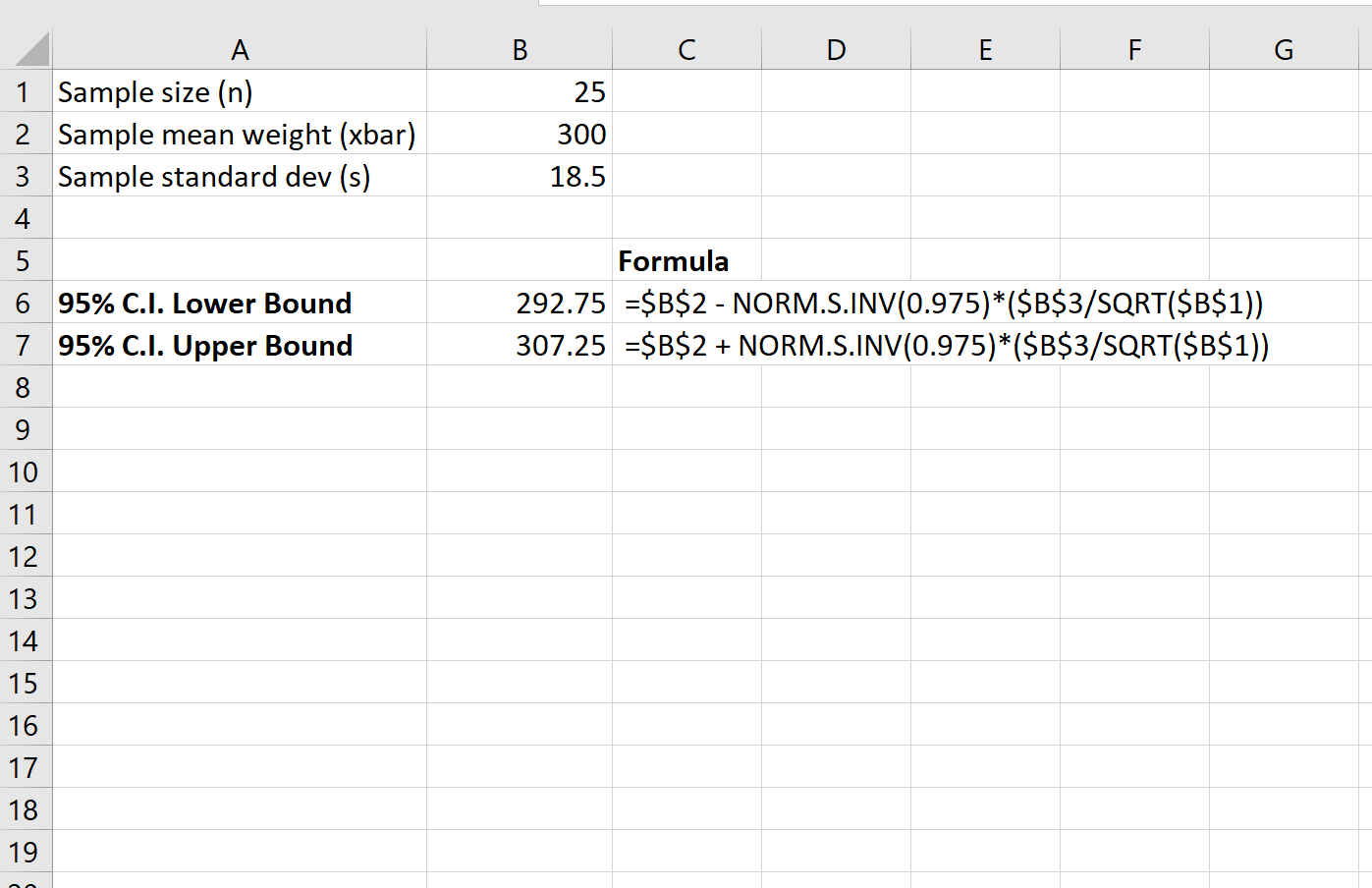
वास्तविक माध्य कछुए की आबादी के वजन के लिए 95% विश्वास अंतराल [292.75, 307.25] है।

उदाहरण 2: साधनों में अंतर के लिए कॉन्फिडेंस अंतराल

जनसंख्या में अंतर के लिए आत्मविश्वास अंतराल की गणना करने के लिए हम निम्नलिखित सूत्र का उपयोग करते हैं:

आत्मविश्वास अंतराल = ( x ₁ – x ₂ ) +/- t*√((s _p ² /n ₁ ) + (s _p ² /n ₂ ))

सोना:

• x ₁ , x ₂ : नमूना 1 का माध्य, नमूना 2 का माध्य
• टी: आत्मविश्वास के स्तर और (एन ₁ + एन ₂ -2) स्वतंत्रता की डिग्री के आधार पर टी-महत्वपूर्ण मूल्य
• एस _पी ² : एकत्रित विचरण, ((एन ₁ -1)एस ₁ ² + (एन ₂ -1)एस ₂ ² ) / (एन ₁ +एन ₂ -2) के रूप में गणना की गई
• टी: टी-क्रिटिकल मान
• एन ₁ , एन ₂ : नमूना आकार 1, नमूना आकार 2

उदाहरण: मान लीजिए कि हम कछुओं की दो अलग-अलग प्रजातियों के बीच औसत वजन के अंतर का अनुमान लगाना चाहते हैं। इसलिए हम प्रत्येक आबादी से 15 कछुओं का एक यादृच्छिक नमूना एकत्र करते हैं। यहां प्रत्येक नमूने का सारांश डेटा दिया गया है:

नमूना 1:

• x1 = ₃₁₀
• एस ₁ = 18.5
• एन ₁ = 15

नमूना 2:

• x2 ₌ 300
• _एस2 = 16.4
• _n2 = 15

निम्नलिखित स्क्रीनशॉट दिखाता है कि जनसंख्या में वास्तविक अंतर के लिए 95% विश्वास अंतराल की गणना कैसे करें:

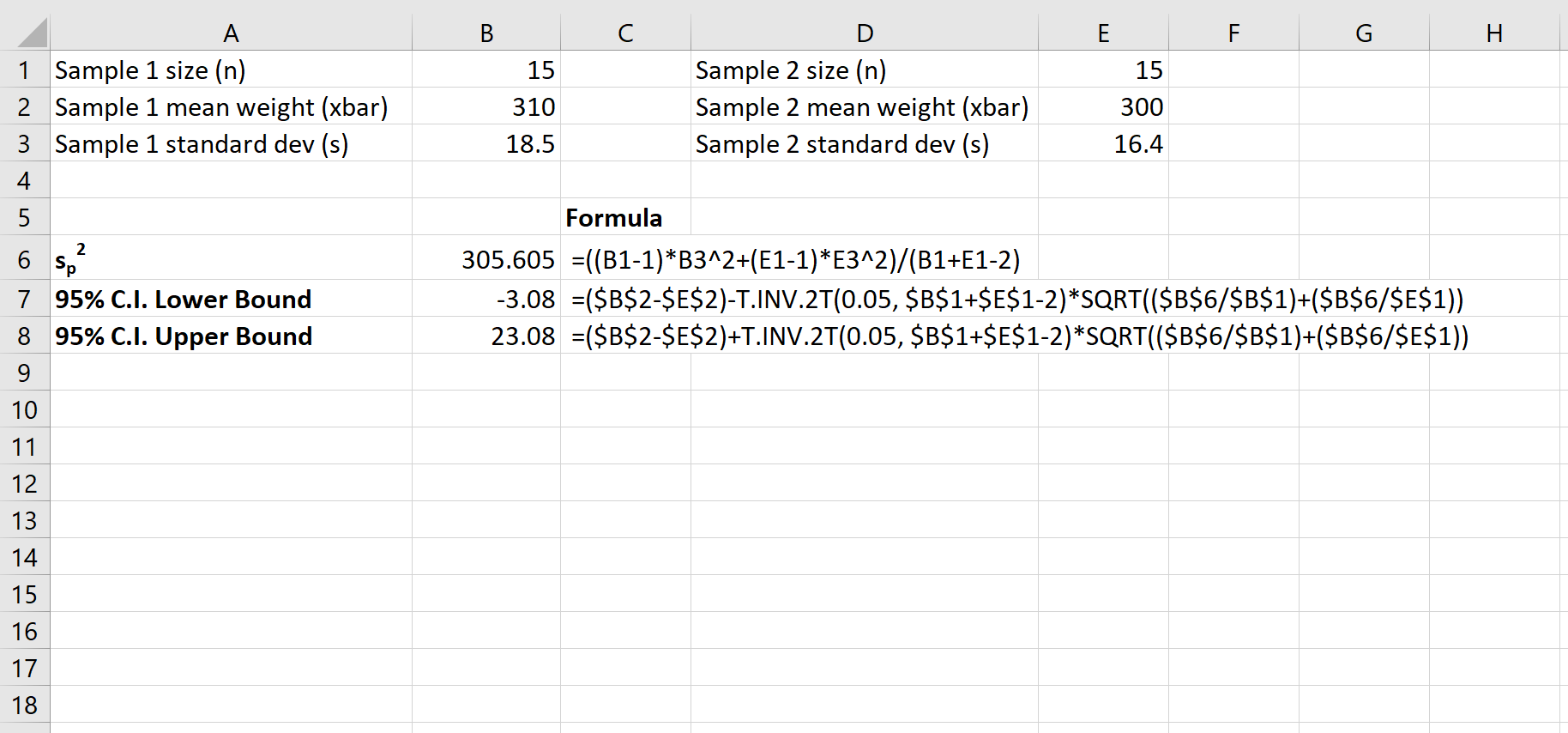
जनसंख्या साधनों के बीच वास्तविक अंतर के लिए 95% विश्वास अंतराल [-3.08, 23.08] है।

उदाहरण 3: किसी अनुपात के लिए विश्वास अंतराल

किसी अनुपात के लिए विश्वास अंतराल की गणना करने के लिए हम निम्नलिखित सूत्र का उपयोग करते हैं:

आत्मविश्वास अंतराल = p +/- z*√ p(1-p) / n

सोना:

• पी: नमूना अनुपात
• z: चुना हुआ z मान
• n: नमूना आकार

उदाहरण: मान लीजिए कि हम किसी काउंटी में उन निवासियों के अनुपात का अनुमान लगाना चाहते हैं जो एक निश्चित कानून का समर्थन करते हैं। हम 100 निवासियों का एक यादृच्छिक नमूना चुनते हैं और उनसे पूछते हैं कि कानून पर उनकी स्थिति क्या है। यहाँ परिणाम हैं:

• नमूना आकार n = 100
• कानून के पक्ष में अनुपात पी = 0.56

निम्नलिखित स्क्रीनशॉट दिखाता है कि कानून का समर्थन करने वाले काउंटीव्यापी निवासियों के वास्तविक अनुपात के लिए 95% विश्वास अंतराल की गणना कैसे करें:

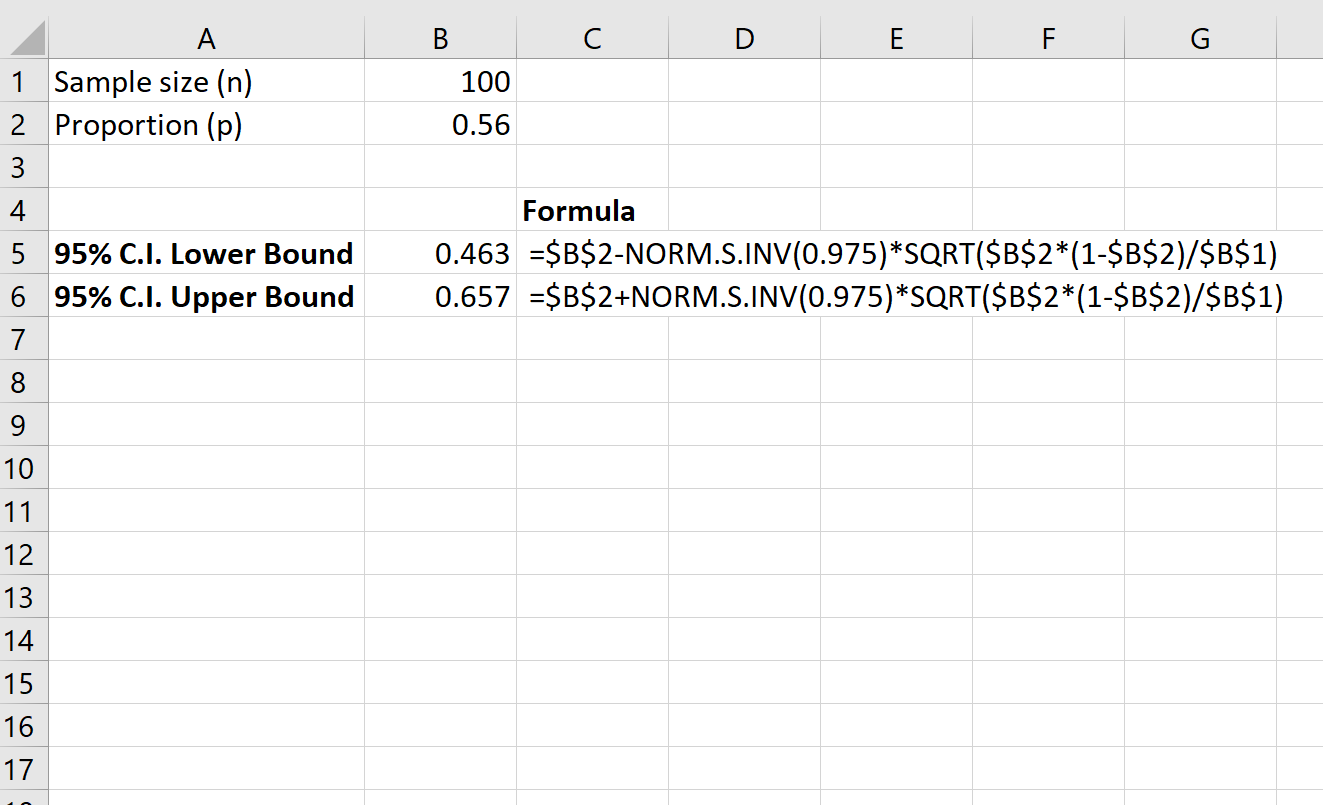
पूरे देश में कानून का समर्थन करने वाले निवासियों के वास्तविक अनुपात के लिए 95% विश्वास अंतराल [.463, .657] है।

उदाहरण 4: अनुपात में अंतर के लिए कॉन्फिडेंस अंतराल

अनुपातों में अंतर के लिए विश्वास अंतराल की गणना करने के लिए हम निम्नलिखित सूत्र का उपयोग करते हैं:

आत्मविश्वास अंतराल = (पी ₁ -पी ₂ ) +/- जेड*√(पी ₁ (1-पी ₁ )/एन ₁ + पी ₂ (1-पी ₂ )/एन ₂ )

सोना:

• पी ₁ , पी ₂ : नमूना 1 का अनुपात, नमूना 2 का अनुपात
• z: आत्मविश्वास के स्तर पर आधारित z-महत्वपूर्ण मान
• एन ₁ , एन ₂ : नमूना आकार 1, नमूना आकार 2

उदाहरण: मान लीजिए कि हम काउंटी ए में एक निश्चित कानून का समर्थन करने वाले निवासियों के अनुपात की तुलना में काउंटी बी में कानून का समर्थन करने वाले निवासियों के अनुपात के बीच अंतर का अनुमान लगाना चाहते हैं। यहां प्रत्येक नमूने के लिए सारांश डेटा दिया गया है:

नमूना 1:

• एन ₁ = 100
• पी ₁ = 0.62 (अर्थात 100 में से 62 निवासी कानून का समर्थन करते हैं)

नमूना 2:

• _n2 = 100
• पी ₂ = 0.46 (अर्थात् 100 में से 46 निवासी कानून का समर्थन करते हैं)

निम्नलिखित स्क्रीनशॉट दिखाता है कि काउंटियों के बीच कानून का समर्थन करने वाले निवासियों के अनुपात में वास्तविक अंतर के लिए 95% विश्वास अंतराल की गणना कैसे करें:

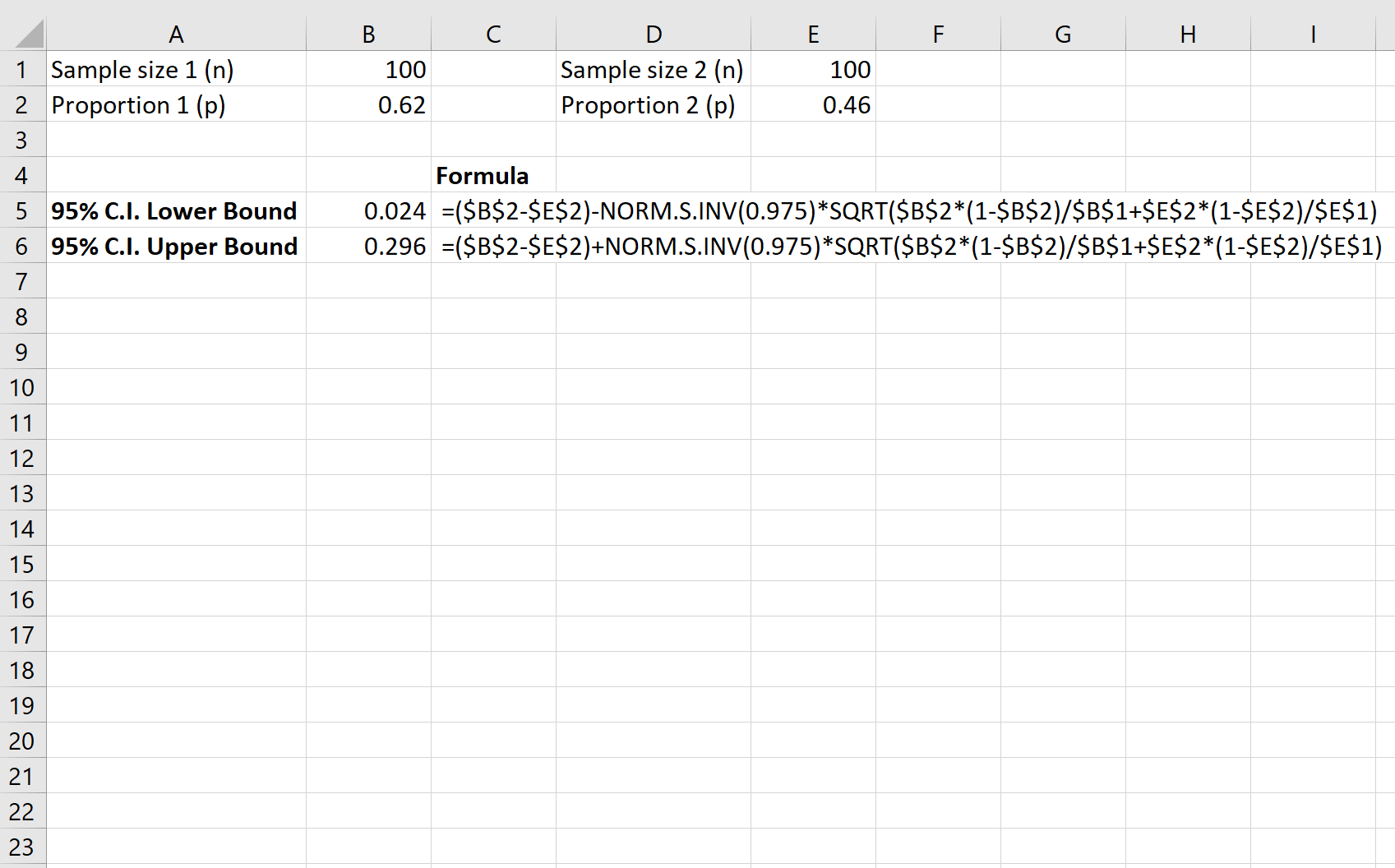
काउंटियों के बीच कानून का समर्थन करने वाले निवासियों के अनुपात में वास्तविक अंतर के लिए 9.5% विश्वास अंतराल [0.024, 0.296] है।

आप यहां अधिक एक्सेल ट्यूटोरियल पा सकते हैं।