रैखिक मॉडलों को फिट करने के लिए r में lm() फ़ंक्शन का उपयोग कैसे करें

R में lm() फ़ंक्शन का उपयोग रैखिक प्रतिगमन मॉडल को फिट करने के लिए किया जाता है।

यह फ़ंक्शन निम्नलिखित मूल सिंटैक्स का उपयोग करता है:

एलएम(सूत्र, डेटा,…)

सोना:

• सूत्र: रैखिक मॉडल सूत्र (जैसे y ~ x1 + x2)
• डेटा: डेटा ब्लॉक का नाम जिसमें डेटा है

निम्न उदाहरण दिखाता है कि निम्न कार्य करने के लिए R में इस फ़ंक्शन का उपयोग कैसे करें:

• एक प्रतिगमन मॉडल फ़िट करें
• प्रतिगमन मॉडल फ़िट सारांश देखें
• मॉडल डायग्नोस्टिक प्लॉट देखें
• फिट किए गए प्रतिगमन मॉडल को प्लॉट करें
• प्रतिगमन मॉडल का उपयोग करके पूर्वानुमान लगाएं

प्रतिगमन मॉडल फिट करें

निम्नलिखित कोड दिखाता है कि आर में एक रैखिक प्रतिगमन मॉडल को फिट करने के लिए एलएम() फ़ंक्शन का उपयोग कैसे करें:

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

प्रतिगमन मॉडल सारांश दिखाएँ

फिर हम प्रतिगमन मॉडल फिट का सारांश प्रदर्शित करने के लिए सारांश() फ़ंक्शन का उपयोग कर सकते हैं:

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

यहां मॉडल में सबसे महत्वपूर्ण मूल्यों की व्याख्या करने का तरीका बताया गया है:

• एफ-सांख्यिकी = 18.35, संगत पी-मान = 0.002675। चूँकि यह पी-वैल्यू 0.05 से कम है, इसलिए समग्र रूप से मॉडल सांख्यिकीय रूप से महत्वपूर्ण है।
• एकाधिक आर वर्ग = 0.6964। यह हमें बताता है कि प्रतिक्रिया चर, y में 69.64% भिन्नता को भविष्यवक्ता चर, x द्वारा समझाया जा सकता है।
• x का अनुमानित गुणांक : 1.2780. यह हमें बताता है कि x में प्रत्येक अतिरिक्त इकाई वृद्धि y में 1.2780 की औसत वृद्धि से जुड़ी है।

फिर हम अनुमानित प्रतिगमन समीकरण लिखने के लिए आउटपुट से गुणांक अनुमान का उपयोग कर सकते हैं:

y = 11.1432 + 1.2780*(x)

बोनस : आप यहां आर में प्रतिगमन आउटपुट के प्रत्येक मूल्य की व्याख्या करने के लिए एक संपूर्ण मार्गदर्शिका पा सकते हैं।

मॉडल डायग्नोस्टिक प्लॉट देखें

फिर हम प्रतिगमन मॉडल के डायग्नोस्टिक प्लॉट को प्लॉट करने के लिए प्लॉट() फ़ंक्शन का उपयोग कर सकते हैं:

 #create diagnostic plots
plot(model) 

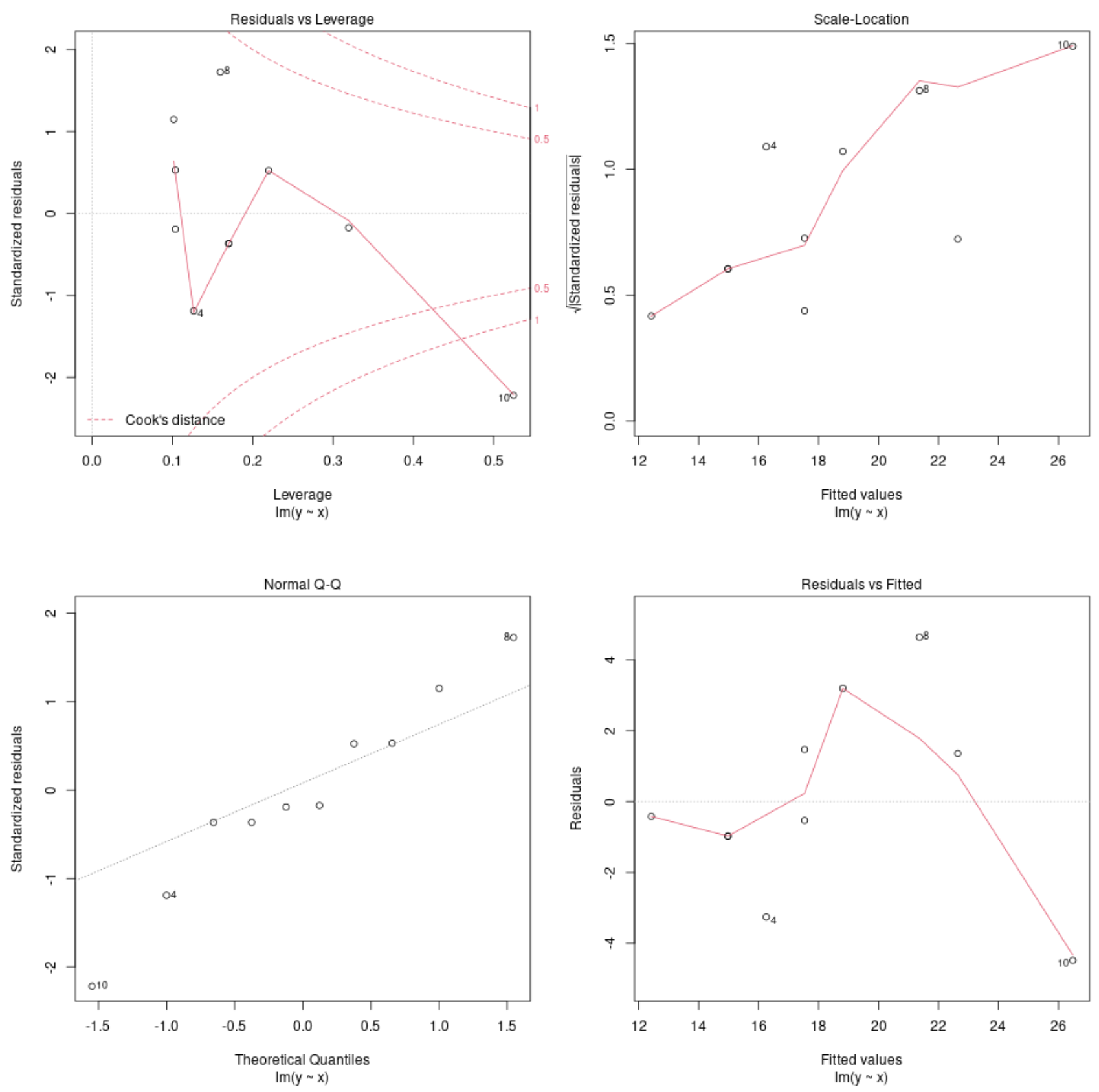
ये ग्राफ़ हमें यह निर्धारित करने के लिए प्रतिगमन मॉडल के अवशेषों का विश्लेषण करने की अनुमति देते हैं कि मॉडल डेटा के लिए उपयोग करने के लिए उपयुक्त है या नहीं।

आर में किसी मॉडल के डायग्नोस्टिक प्लॉट की व्याख्या कैसे करें, इसकी संपूर्ण व्याख्या के लिए इस ट्यूटोरियल का संदर्भ लें।

फिट किए गए प्रतिगमन मॉडल को प्लॉट करें

फिटेड रिग्रेशन मॉडल को प्लॉट करने के लिए हम abline() फ़ंक्शन का उपयोग कर सकते हैं:

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

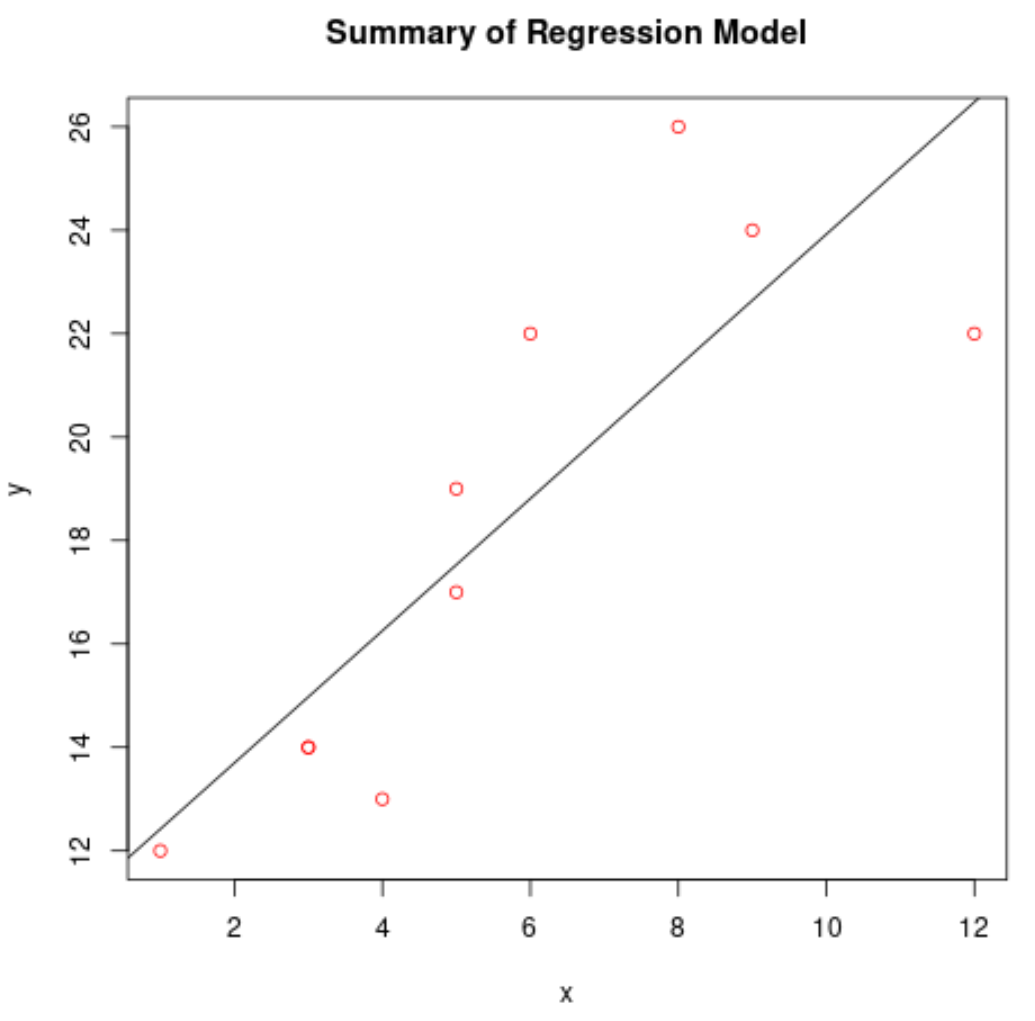
पूर्वानुमान लगाने के लिए प्रतिगमन मॉडल का उपयोग करें

हम किसी नए अवलोकन के लिए प्रतिक्रिया मूल्य की भविष्यवाणी करने के लिए पूर्वानुमान () फ़ंक्शन का उपयोग कर सकते हैं:

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

मॉडल का अनुमान है कि इस नए अवलोकन का प्रतिक्रिया मूल्य 17.5332 होगा।

अतिरिक्त संसाधन

आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में चरणबद्ध प्रतिगमन कैसे करें