आर में डायग्नोस्टिक प्लॉट की व्याख्या कैसे करें

रैखिक प्रतिगमन मॉडल का उपयोग एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध का वर्णन करने के लिए किया जाता है।

हालाँकि, एक बार जब हम एक प्रतिगमन मॉडल फिट कर लेते हैं, तो मॉडल के अवशेषों का विश्लेषण करने के लिए डायग्नोस्टिक प्लॉट भी तैयार करना एक अच्छा विचार है और यह सुनिश्चित करना है कि जिस विशेष डेटा के साथ हम काम कर रहे हैं, उसके लिए एक रैखिक मॉडल का उपयोग करना उचित है।

यह ट्यूटोरियल बताता है कि आर में दिए गए रिग्रेशन मॉडल के लिए डायग्नोस्टिक प्लॉट कैसे बनाएं और व्याख्या करें।

उदाहरण: आर में डायग्नोस्टिक प्लॉट बनाएं और व्याख्या करें

मान लीजिए कि हम एक निश्चित कक्षा में छात्रों के “परीक्षा ग्रेड” की भविष्यवाणी करने के लिए “अध्ययन के घंटे” का उपयोग करके एक सरल रैखिक प्रतिगमन मॉडल फिट करते हैं:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

हम इस प्रतिगमन मॉडल के लिए चार डायग्नोस्टिक प्लॉट तैयार करने के लिए प्लॉट() कमांड का उपयोग कर सकते हैं:

 #produce diagnostic plots for regression model
plot(model)

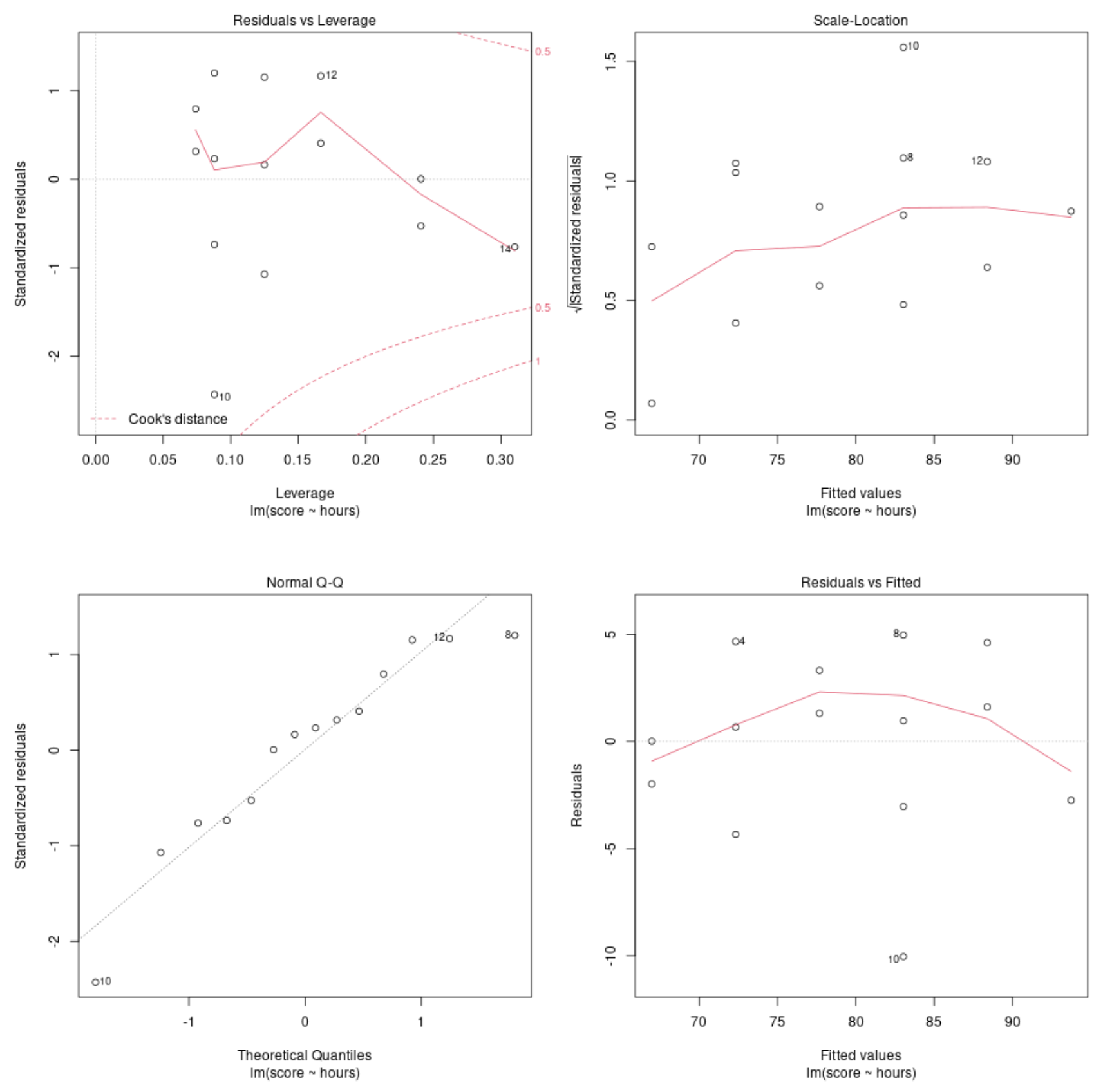
डायग्नोस्टिक चार्ट #1: अवशेष बनाम। उत्तोलन चार्ट

इस ग्राफ़ का उपयोग प्रभावशाली अवलोकनों की पहचान करने के लिए किया जाता है। यदि इस ग्राफ़ पर कोई भी बिंदु कुक की दूरी (बिंदीदार रेखाओं) से बाहर आता है, तो यह एक प्रभावशाली अवलोकन है।

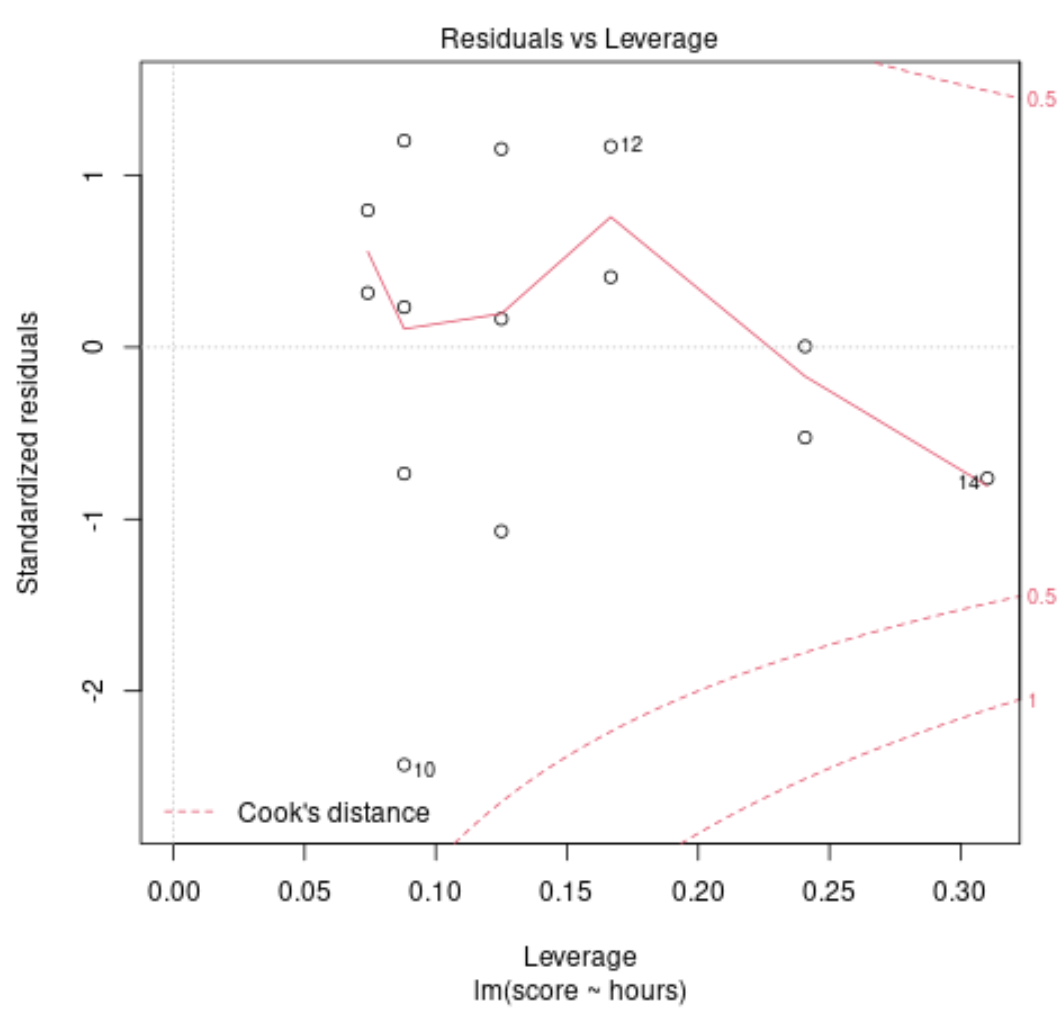
हमारे उदाहरण में, हम देख सकते हैं कि अवलोकन #10 कुक दूरी सीमा के सबसे करीब है, लेकिन यह बिंदीदार रेखा से बाहर नहीं आता है। इसका मतलब यह है कि हमारे डेटासेट में कोई अत्यधिक प्रभावशाली बिंदु नहीं हैं।

डायग्नोस्टिक प्लॉट #2: स्केल और लोकेशन प्लॉट

इस ग्राफ़ का उपयोग हमारे प्रतिगमन मॉडल के अवशेषों के बीच विचरण की समानता (जिसे “होमोस्केडैस्टिसिटी” भी कहा जाता है) की धारणा को सत्यापित करने के लिए किया जाता है। यदि प्लॉट पर लाल रेखा लगभग क्षैतिज है, तो समान विचरण की धारणा संभवतः पूरी होती है।

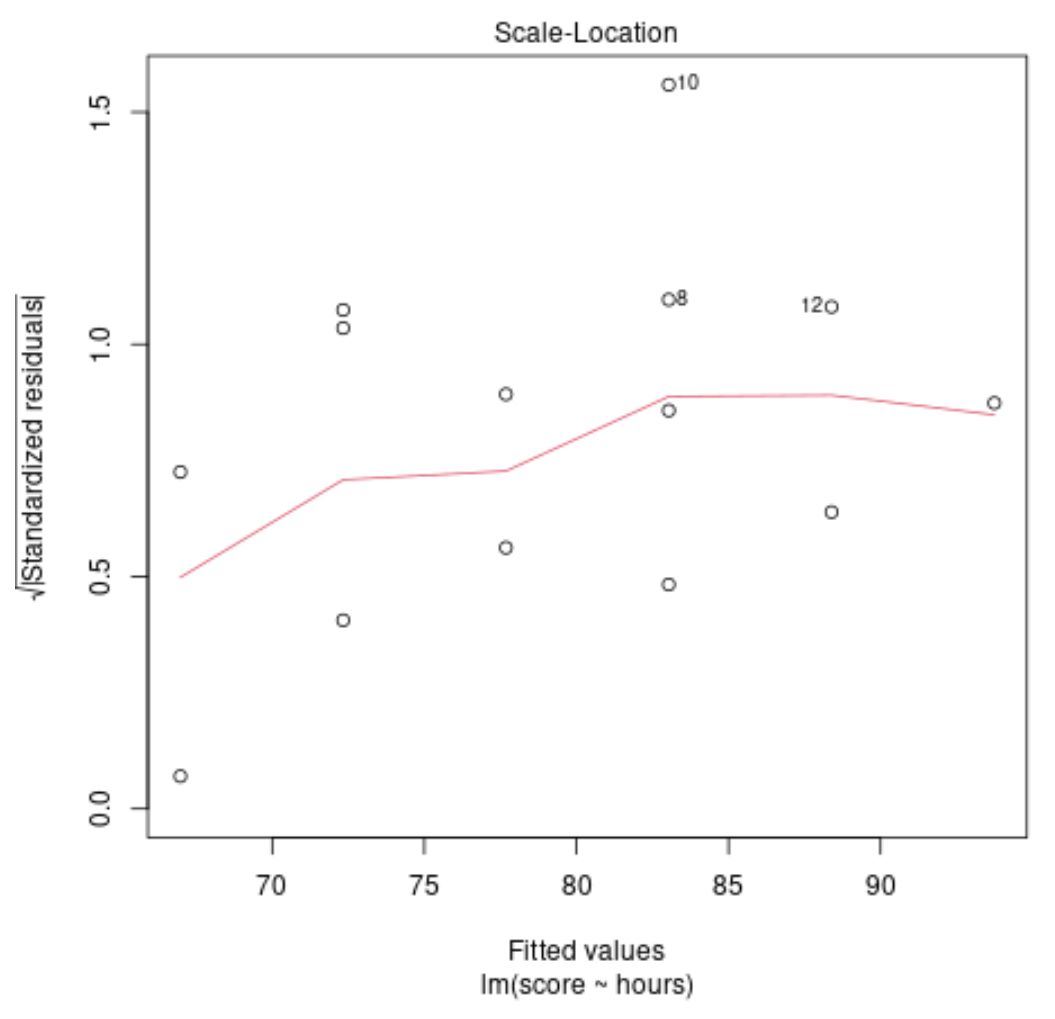
हमारे उदाहरण में, हम देख सकते हैं कि लाल रेखा प्लॉट पर बिल्कुल क्षैतिज नहीं है, लेकिन यह किसी भी बिंदु पर बहुत अधिक विचलन नहीं करती है। हम संभवतः यह कहते हैं कि इस मामले में समान विचरण की धारणा का उल्लंघन नहीं किया गया है।

संबंधित: प्रतिगमन विश्लेषण में विषमलैंगिकता को समझना

डायग्नोस्टिक ट्रेस #3: सामान्य QQ ट्रेस

इस प्लॉट का उपयोग यह निर्धारित करने के लिए किया जाता है कि प्रतिगमन मॉडल के अवशेष सामान्य रूप से वितरित हैं या नहीं। यदि इस ग्राफ़ पर बिंदु लगभग एक सीधी विकर्ण रेखा पर स्थित हैं, तो हम मान सकते हैं कि अवशेष सामान्य रूप से वितरित हैं।

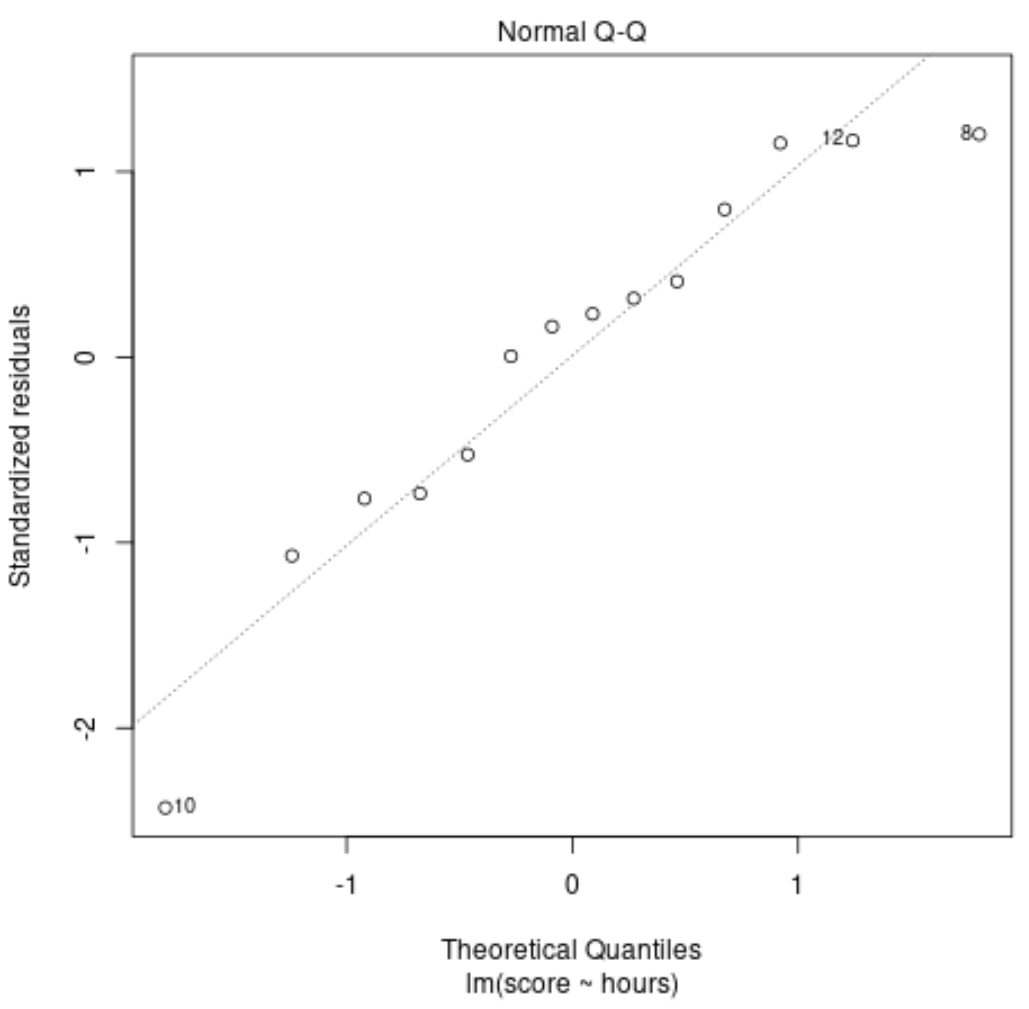
हमारे उदाहरण में, हम देख सकते हैं कि बिंदु लगभग विकर्ण सीधी रेखा के अनुदिश स्थित हैं। अवलोकन #10 और #8 सिरों पर रेखा से थोड़ा विचलित हैं, लेकिन यह घोषित करने के लिए पर्याप्त नहीं हैं कि अवशेष सामान्य रूप से वितरित नहीं हैं।

डायग्नोस्टिक प्लॉट #4: अवशेष बनाम। समायोजित प्लॉट

इस प्लॉट का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या अवशेष गैर-रेखीय पैटर्न प्रदर्शित करते हैं। यदि प्लॉट के केंद्र में लाल रेखा लगभग क्षैतिज है, तो हम मान सकते हैं कि अवशेष एक रैखिक पैटर्न का पालन करते हैं।

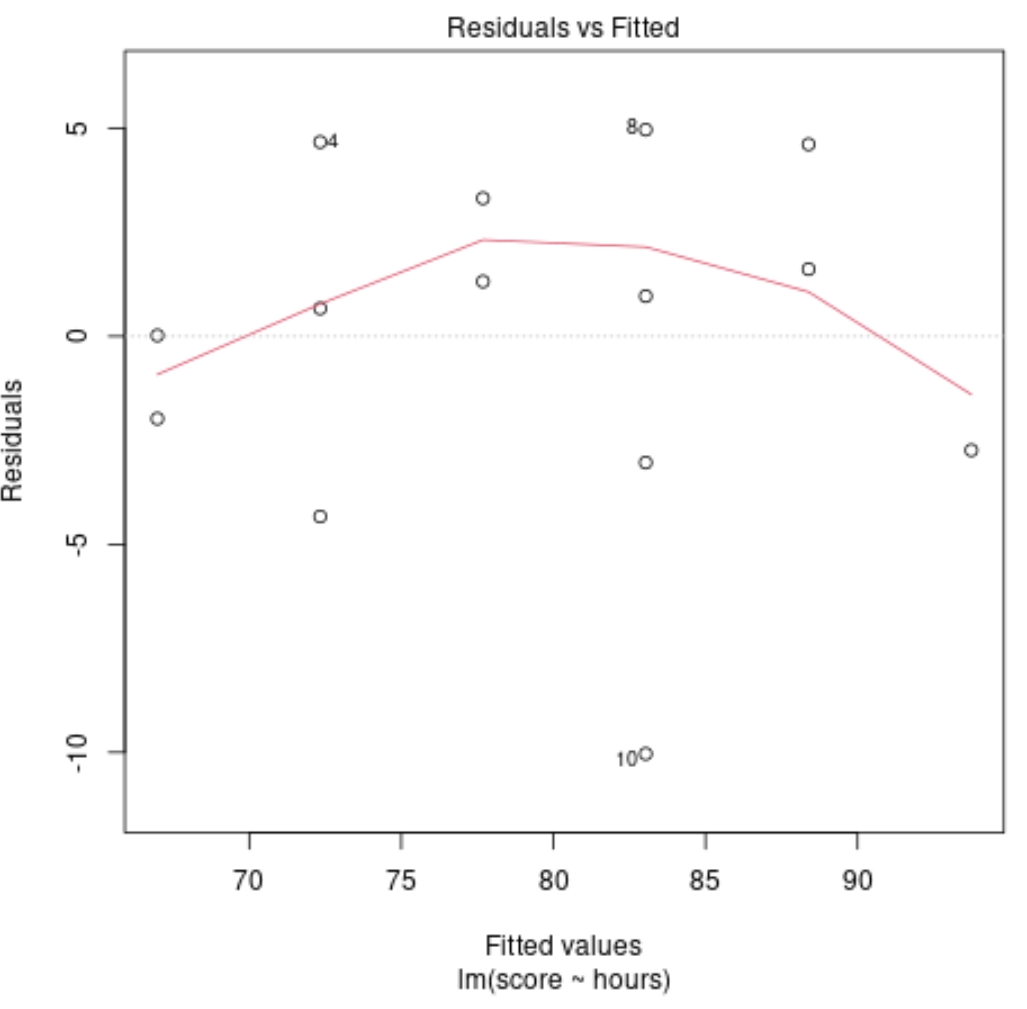
हमारे उदाहरण में, हम देख सकते हैं कि लाल रेखा एक पूर्ण क्षैतिज रेखा से विचलित होती है लेकिन महत्वपूर्ण रूप से नहीं। हम संभवतः यह कह रहे हैं कि अवशेष मोटे तौर पर रैखिक पैटर्न का पालन करते हैं और इस डेटा सेट के लिए एक रैखिक प्रतिगमन मॉडल उपयुक्त है।

अतिरिक्त संसाधन

रैखिक प्रतिगमन की चार धारणाएँ
सांख्यिकी में अवशेष क्या हैं?
आर में अवशिष्ट प्लॉट कैसे बनाएं
स्केल और स्थान प्लॉट की व्याख्या कैसे करें