आर में द्विचर विश्लेषण कैसे करें (उदाहरण के साथ)

द्विचर विश्लेषण शब्द का तात्पर्य दो चरों के विश्लेषण से है। आप इसे याद रख सकते हैं क्योंकि उपसर्ग “द्वि” का अर्थ “दो” है।

द्विचर विश्लेषण का लक्ष्य दो चरों के बीच संबंध को समझना है

द्विचर विश्लेषण करने के तीन सामान्य तरीके हैं:

1. बिंदु बादल

2. सहसंबंध गुणांक

3. सरल रेखीय प्रतिगमन

निम्नलिखित उदाहरण दर्शाता है कि निम्नलिखित डेटा सेट का उपयोग करके इनमें से प्रत्येक प्रकार के द्विचर विश्लेषण को कैसे निष्पादित किया जाए जिसमें दो चर पर जानकारी शामिल है: (1) अध्ययन में बिताए गए घंटे और (2) 20 अलग-अलग छात्रों द्वारा अर्जित टेस्ट स्कोर:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. बिंदु बादल

हम आर में परीक्षा ग्रेड बनाम अध्ययन किए गए घंटों का स्कैटरप्लॉट बनाने के लिए निम्नलिखित वाक्यविन्यास का उपयोग कर सकते हैं:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

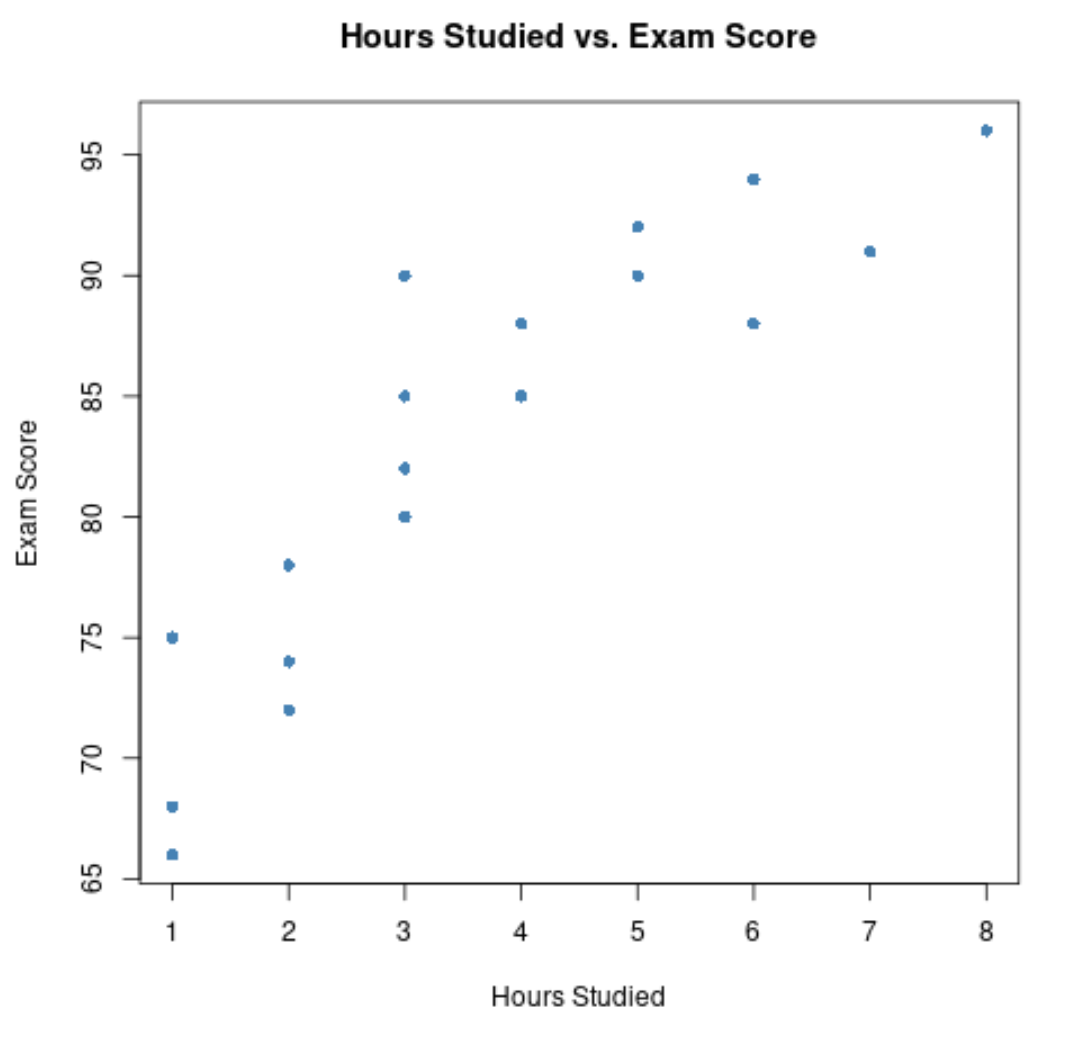
x-अक्ष अध्ययन किए गए घंटों को दर्शाता है और y-अक्ष परीक्षा में अर्जित ग्रेड को दर्शाता है।

ग्राफ़ दर्शाता है कि दोनों चरों के बीच एक सकारात्मक संबंध है: जैसे-जैसे अध्ययन के घंटों की संख्या बढ़ती है, परीक्षा के अंक भी बढ़ने लगते हैं।

2. सहसंबंध गुणांक

पियर्सन सहसंबंध गुणांक दो चर के बीच रैखिक संबंध को मापने का एक तरीका है।

हम दो चरों के बीच पियर्सन सहसंबंध गुणांक की गणना करने के लिए R में cor() फ़ंक्शन का उपयोग कर सकते हैं:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

सहसंबंध गुणांक 0.891 निकला।

यह मान 1 के करीब है, जो अध्ययन किए गए घंटों और परीक्षा ग्रेड के बीच एक मजबूत सकारात्मक सहसंबंध दर्शाता है।

3. सरल रेखीय प्रतिगमन

सरल रेखीय प्रतिगमन एक सांख्यिकीय विधि है जिसका उपयोग हम उस रेखा के समीकरण को खोजने के लिए कर सकते हैं जो डेटा के एक सेट को सबसे अच्छी तरह से “फिट” करता है, जिसका उपयोग हम दो चर के बीच सटीक संबंध को समझने के लिए कर सकते हैं।

हम अध्ययन किए गए घंटों और प्राप्त परीक्षा परिणामों के लिए एक सरल रैखिक प्रतिगमन मॉडल को फिट करने के लिए आर में एलएम () फ़ंक्शन का उपयोग कर सकते हैं:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

फिट किया गया प्रतिगमन समीकरण इस प्रकार है:

परीक्षा स्कोर = 69.0734 + 3.8471*(अध्ययन के घंटे)

यह हमें बताता है कि अध्ययन किया गया प्रत्येक अतिरिक्त घंटा परीक्षा स्कोर में औसतन 3.8471 की वृद्धि से जुड़ा है।

हम अध्ययन किए गए घंटों की कुल संख्या के आधार पर एक छात्र को प्राप्त होने वाले स्कोर की भविष्यवाणी करने के लिए फिट किए गए प्रतिगमन समीकरण का भी उपयोग कर सकते हैं।

उदाहरण के लिए, एक छात्र जो 3 घंटे पढ़ाई करता है उसे 81.6147 का स्कोर मिलना चाहिए:

• परीक्षा स्कोर = 69.0734 + 3.8471*(अध्ययन के घंटे)
• परीक्षा स्कोर = 69.0734 + 3.8471*(3)
• परीक्षा परिणाम = 81.6147

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल द्विचर विश्लेषण के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

द्विचर विश्लेषण का एक परिचय
वास्तविक जीवन में द्विचर डेटा के 5 उदाहरण
सरल रेखीय प्रतिगमन का एक परिचय