आर में बूटस्ट्रैपिंग कैसे करें (उदाहरण के साथ)
बूटस्ट्रैपिंग एक ऐसी विधि है जिसका उपयोग किसी भी आँकड़े की मानक त्रुटि का अनुमान लगाने और आँकड़ों के लिए एक विश्वास अंतराल उत्पन्न करने के लिए किया जा सकता है।
बूटस्ट्रैपिंग की मूल प्रक्रिया इस प्रकार है:
- किसी दिए गए डेटा सेट से प्रतिस्थापन के साथ k प्रतिकृति नमूने लें।
- प्रत्येक नमूने के लिए, रुचि के आँकड़े की गणना करें।
- यह किसी दिए गए आँकड़े के लिए अलग -अलग अनुमान देता है, जिसका उपयोग आप आँकड़ों की मानक त्रुटि की गणना करने और आँकड़ों के लिए एक विश्वास अंतराल बनाने के लिए कर सकते हैं।
हम बूटस्ट्रैप लाइब्रेरी से निम्नलिखित फ़ंक्शंस का उपयोग करके आर में बूटस्ट्रैप कर सकते हैं:
1. बूटस्ट्रैप नमूने तैयार करें।
बूट(डेटा, सांख्यिकी, आर,…)
सोना:
- डेटा: एक वेक्टर, मैट्रिक्स या डेटा का ब्लॉक
- आँकड़ा: एक फ़ंक्शन जो आरंभ किए जाने वाले आँकड़े उत्पन्न करता है
- ए: बूटस्ट्रैप दोहराव की संख्या
2. बूटस्ट्रैप विश्वास अंतराल उत्पन्न करें।
Boot.ci(बूट ऑब्जेक्ट, कॉन्फ़, प्रकार)
सोना:
- बूटऑब्जेक्ट: बूट() फ़ंक्शन द्वारा लौटाया गया ऑब्जेक्ट
- conf: गणना करने के लिए आत्मविश्वास अंतराल। डिफ़ॉल्ट मान 0.95 है
- प्रकार: गणना करने के लिए आत्मविश्वास अंतराल का प्रकार। विकल्पों में ‘स्टैंडर्ड’, ‘बेसिक’, ‘स्टड’, ‘पर्क’, ‘बीसीए’ और ‘ऑल’ शामिल हैं – डिफ़ॉल्ट ‘ऑल’ है
निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में इन कार्यों का उपयोग कैसे करें।
उदाहरण 1: एकल आँकड़ा बूटस्ट्रैप करें
निम्नलिखित कोड दिखाता है कि एक साधारण रैखिक प्रतिगमन मॉडल के आर-वर्ग के लिए मानक त्रुटि की गणना कैसे करें:
set.seed(0) library (boot) #define function to calculate R-squared rsq_function <- function (formula, data, indices) { d <- data[indices,] #allows boot to select sample fit <- lm(formula, data=d) #fit regression model return (summary(fit)$r.square) #return R-squared of model } #perform bootstrapping with 2000 replications reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp) #view results of boostrapping reps ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ available) Bootstrap Statistics: original bias std. error t1* 0.7183433 0.002164339 0.06513426
परिणामों से हम देख सकते हैं:
- इस प्रतिगमन मॉडल के लिए अनुमानित आर-वर्ग 0.7183433 है।
- इस अनुमान के लिए मानक त्रुटि 0.06513426 है।
हम बूटस्ट्रैप्ड नमूनों के वितरण की भी शीघ्रता से कल्पना कर सकते हैं:
plot(reps)
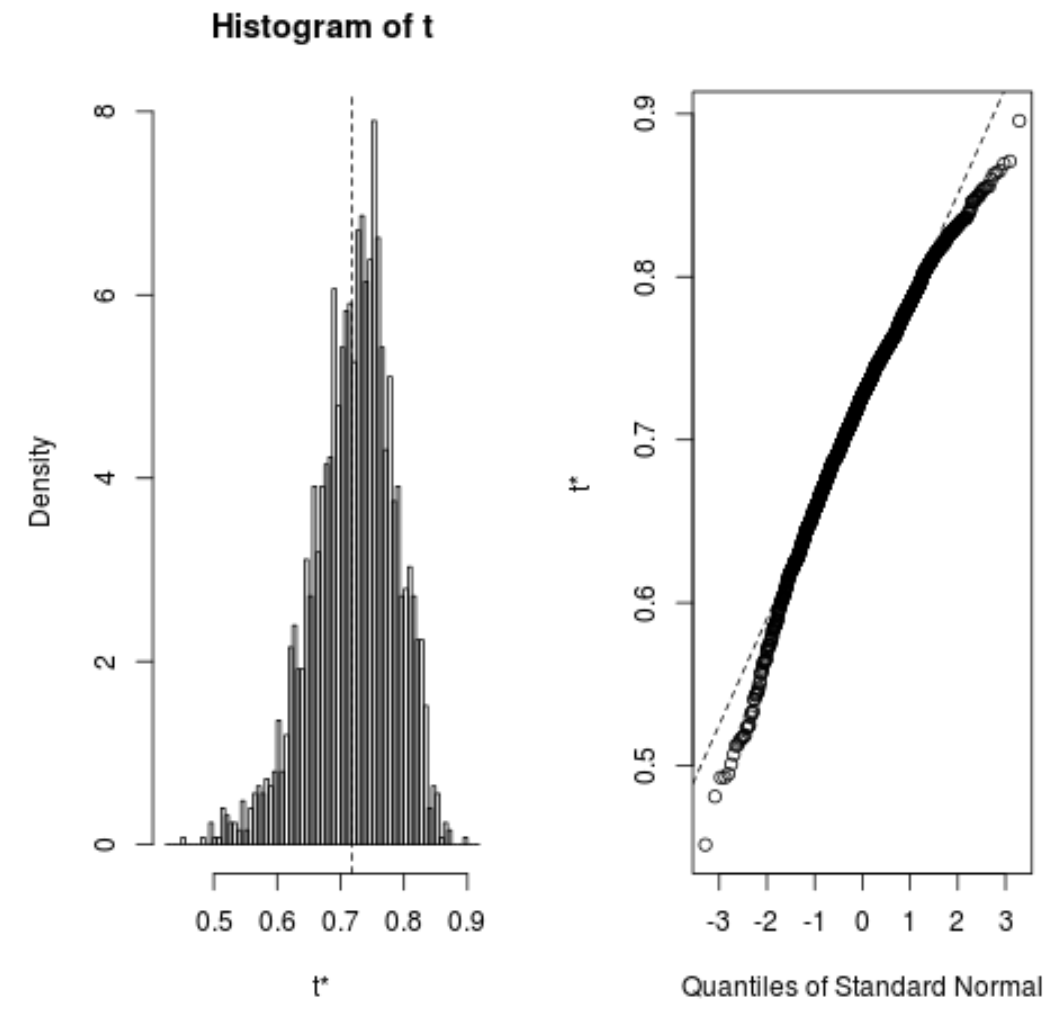
हम मॉडल के अनुमानित आर-वर्ग के लिए 95% विश्वास अंतराल की गणना करने के लिए निम्नलिखित कोड का भी उपयोग कर सकते हैं:
#calculate adjusted bootstrap percentile (BCa) interval boot.ci(reps, type=" bca ") CALL: boot.ci(boot.out = reps, type = "bca") Intervals: Level BCa 95% (0.5350, 0.8188) Calculations and Intervals on Original Scale
परिणाम से, हम देख सकते हैं कि वास्तविक आर-वर्ग मानों के लिए बूटस्ट्रैप्ड 95% विश्वास अंतराल (0.5350, 0.8188) है।
उदाहरण 2: बूटस्ट्रैप एकाधिक आँकड़े
निम्नलिखित कोड दिखाता है कि एकाधिक रैखिक प्रतिगमन मॉडल में प्रत्येक गुणांक के लिए मानक त्रुटि की गणना कैसे करें:
set.seed(0) library (boot) #define function to calculate fitted regression coefficients coef_function <- function (formula, data, indices) { d <- data[indices,] #allows boot to select sample fit <- lm(formula, data=d) #fit regression model return (coef(fit)) #return coefficient estimates of model } #perform bootstrapping with 2000 replications reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp) #view results of boostrapping reps ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ available) Bootstrap Statistics: original bias std. error t1* 29.59985476 -5.058601e-02 1.49354577 t2* -0.04121512 6.549384e-05 0.00527082
परिणामों से हम देख सकते हैं:
- मॉडल इंटरसेप्ट के लिए अनुमानित गुणांक 29.59985476 है और इस अनुमान की मानक त्रुटि 1.49354577 है।
- मॉडल में भविष्यवक्ता चर वितरण के लिए अनुमानित गुणांक -0.04121512 है और इस अनुमान की मानक त्रुटि 0.00527082 है।
हम बूटस्ट्रैप्ड नमूनों के वितरण की भी शीघ्रता से कल्पना कर सकते हैं:
plot(reps, index=1) #intercept of model plot(reps, index=2) #disp predictor variable
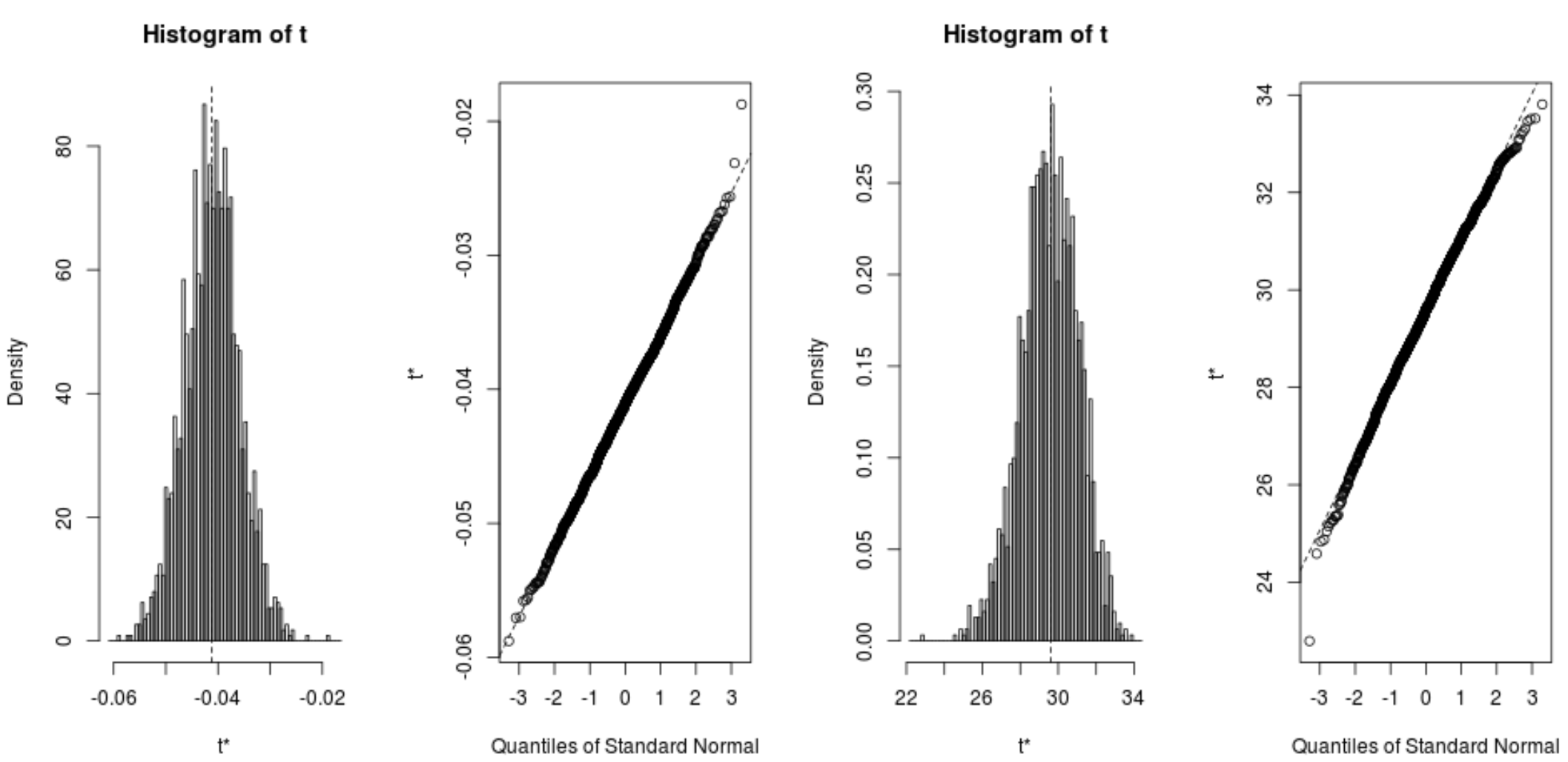
हम प्रत्येक गुणांक के लिए 95% विश्वास अंतराल की गणना करने के लिए निम्नलिखित कोड का भी उपयोग कर सकते हैं:
#calculate adjusted bootstrap percentile (BCa) intervals boot.ci(reps, type=" bca ", index=1) #intercept of model boot.ci(reps, type=" bca ", index=2) #disp predictor variable CALL: boot.ci(boot.out = reps, type = "bca", index = 1) Intervals: Level BCa 95% (26.78, 32.66) Calculations and Intervals on Original Scale BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS Based on 2000 bootstrap replicates CALL: boot.ci(boot.out = reps, type = "bca", index = 2) Intervals: Level BCa 95% (-0.0520, -0.0312) Calculations and Intervals on Original Scale
परिणामों से, हम देख सकते हैं कि मॉडल गुणांक के लिए बूटस्ट्रैप्ड 95% विश्वास अंतराल इस प्रकार हैं:
- अवरोधन के लिए आईसी: (26.78, 32.66)
- वितरण के लिए सीआई: (-.0520, -.0312)
अतिरिक्त संसाधन
आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आत्मविश्वास अंतराल का परिचय