आर में मजबूत प्रतिगमन कैसे करें (चरण दर चरण)

मजबूत प्रतिगमन एक ऐसी विधि है जिसे हम सामान्य न्यूनतम वर्ग प्रतिगमन के विकल्प के रूप में उपयोग कर सकते हैं जब हम जिस डेटासेट के साथ काम कर रहे हैं उसमें आउटलेयर या प्रभावशाली अवलोकन होते हैं।

R में मजबूत प्रतिगमन करने के लिए, हम MASS पैकेज से rlm() फ़ंक्शन का उपयोग कर सकते हैं, जो निम्नलिखित सिंटैक्स का उपयोग करता है:

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि किसी दिए गए डेटासेट के लिए आर में मजबूत प्रतिगमन कैसे करें।

चरण 1: डेटा बनाएं

सबसे पहले, आइए काम करने के लिए एक नकली डेटासेट बनाएं:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

चरण 2: सामान्य न्यूनतम वर्ग प्रतिगमन निष्पादित करें

इसके बाद, आइए एक सामान्य न्यूनतम वर्ग प्रतिगमन मॉडल फिट करें और मानकीकृत अवशेषों का एक प्लॉट बनाएं।

व्यवहार में, हम अक्सर किसी भी मानकीकृत अवशिष्ट पर विचार करते हैं जिसका पूर्ण मूल्य 3 से अधिक है।

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

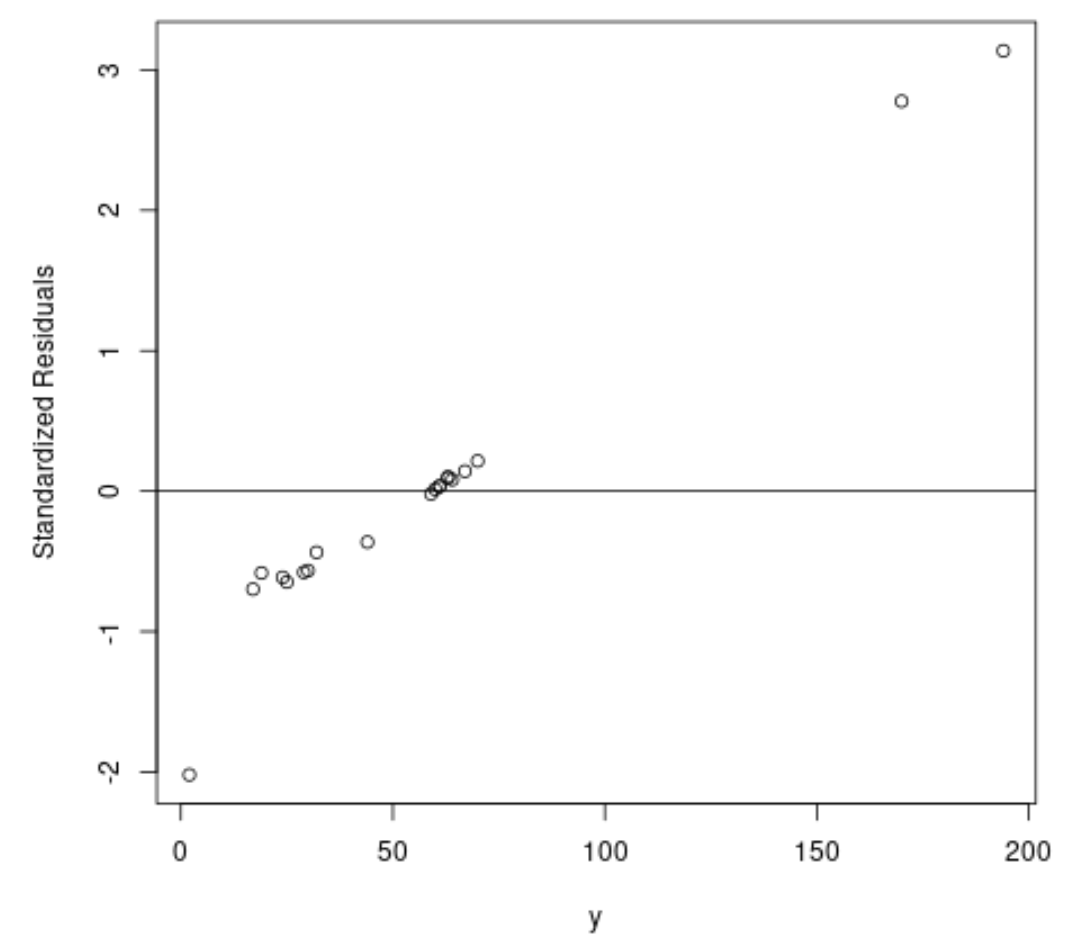
ग्राफ़ से हम देख सकते हैं कि 3 के आसपास मानकीकृत अवशेषों के साथ दो अवलोकन हैं।

यह इंगित करता है कि डेटासेट में दो संभावित आउटलेर हैं और इसलिए हमें इसके बजाय मजबूत प्रतिगमन से लाभ हो सकता है।

चरण 3: मजबूत प्रतिगमन करें

इसके बाद, आइए एक मजबूत प्रतिगमन मॉडल को फिट करने के लिए rlm() फ़ंक्शन का उपयोग करें:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

यह निर्धारित करने के लिए कि क्या यह मजबूत प्रतिगमन मॉडल ओएलएस मॉडल की तुलना में डेटा के लिए बेहतर फिट प्रदान करता है, हम प्रत्येक मॉडल की अवशिष्ट मानक त्रुटि की गणना कर सकते हैं।

अवशिष्ट मानक त्रुटि (आरएसई) एक प्रतिगमन मॉडल में अवशेषों के मानक विचलन को मापने का एक तरीका है। सीएसआर मूल्य जितना कम होगा, मॉडल उतना ही बेहतर डेटा को फिट करने में सक्षम होगा।

निम्नलिखित कोड दिखाता है कि प्रत्येक मॉडल के लिए आरएसई की गणना कैसे करें:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

हम देख सकते हैं कि मजबूत प्रतिगमन मॉडल का आरएसई सामान्य न्यूनतम वर्ग प्रतिगमन मॉडल की तुलना में बहुत कम है, जो हमें बताता है कि मजबूत प्रतिगमन मॉडल डेटा के लिए बेहतर फिट प्रदान करता है।

अतिरिक्त संसाधन

आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में बहुपद प्रतिगमन कैसे करें