आर में मैथ्यूज सहसंबंध गुणांक की गणना कैसे करें

मैथ्यूज सहसंबंध गुणांक (एमसीसी) एक मीट्रिक है जिसका उपयोग हम वर्गीकरण मॉडल के प्रदर्शन का मूल्यांकन करने के लिए कर सकते हैं।

इसकी गणना इस प्रकार की जाती है:

एमसीसी = (टीपी*टीएन – एफपी*एफएन) / √ (टीपी+एफपी)(टीपी+एफएन)(टीएन+एफपी)(टीएन+एफएन)

सोना:

• टीपी : वास्तविक सकारात्मकता की संख्या
• टीएन : सच्चे नकारात्मक की संख्या
• एफपी : गलत सकारात्मकों की संख्या
• एफएन : गलत नकारात्मक की संख्या

यह मीट्रिक विशेष रूप से तब उपयोगी होती है जब दो वर्ग असंतुलित होते हैं, अर्थात, एक वर्ग दूसरे की तुलना में बहुत अधिक दिखाई देता है।

एमसीसी का मान -1 और 1 के बीच है जहां:

• -1 पूर्वानुमानित वर्गों और वास्तविक वर्गों के बीच पूर्ण असहमति को इंगित करता है
• 0 का मतलब पूरी तरह से यादृच्छिक अनुमान है
• 1 पूर्वानुमानित वर्गों और वास्तविक वर्गों के बीच पूर्ण सहमति दर्शाता है

उदाहरण के लिए, मान लीजिए कि एक खेल विश्लेषक यह अनुमान लगाने के लिए एक लॉजिस्टिक रिग्रेशन मॉडल का उपयोग करता है कि 400 अलग-अलग कॉलेज बास्केटबॉल खिलाड़ियों को एनबीए में शामिल किया जाएगा या नहीं।

निम्नलिखित भ्रम मैट्रिक्स मॉडल द्वारा की गई भविष्यवाणियों का सारांश प्रस्तुत करता है:

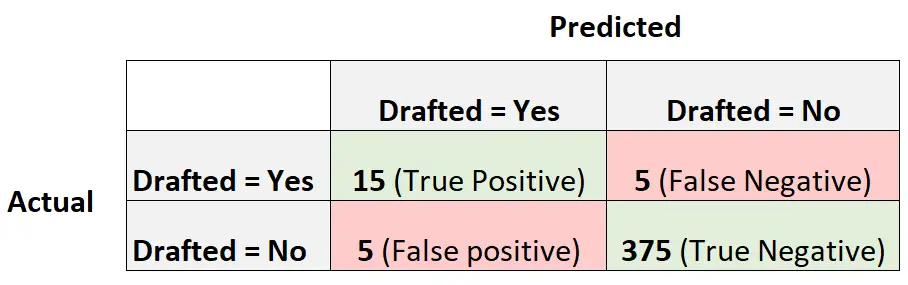
मॉडल के एमसीसी की गणना करने के लिए, हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

• एमसीसी = (टीपी*टीएन – एफपी*एफएन) / √ (टीपी+एफपी)(टीपी+एफएन)(टीएन+एफपी)(टीएन+एफएन)
• एमसीसी = (15*375-5*5) / √ (15+5)(15+5)(375+5)(375+5)
• एमसीसी = 0.7368

मैथ्यूज सहसंबंध गुणांक 0.7368 निकला।

यह मान कुछ हद तक एक के करीब है, जो दर्शाता है कि मॉडल यह भविष्यवाणी करने का अच्छा काम कर रहा है कि खिलाड़ियों को ड्राफ्ट किया जाएगा या नहीं।

निम्नलिखित उदाहरण दिखाता है कि आर में mltools पैकेज से mcc() फ़ंक्शन का उपयोग करके इस विशिष्ट परिदृश्य के लिए MCC की गणना कैसे करें।

उदाहरण: आर में मैथ्यूज सहसंबंध गुणांक की गणना

निम्नलिखित कोड दिखाता है कि पूर्वानुमानित वर्गों के वेक्टर और वास्तविक वर्गों के वेक्टर को कैसे परिभाषित किया जाए, और फिर mltools पैकेज से mcc() फ़ंक्शन का उपयोग करके मैथ्यू सहसंबंध गुणांक की गणना करें:

 library (mltools)

#define vector of actual classes
actual <- rep (c(1, 0), times =c(20, 380))

#define vector of predicted classes
preds <- rep (c(1, 0, 1, 0), times =c(15, 5, 5, 375))

#calculate Matthews correlation coefficient
mcc(preds, actual)

[1] 0.7368421

मैथ्यूज सहसंबंध गुणांक 0.7368 है।

यह उस मूल्य से मेल खाता है जिसकी हमने पहले मैन्युअल रूप से गणना की थी।

यदि आप कन्फ्यूजन मैट्रिक्स के लिए मैथ्यूज सहसंबंध गुणांक की गणना करना चाहते हैं, तो आप कन्फ्यूजनएम तर्क का उपयोग निम्नानुसार कर सकते हैं:

 library (mltools)

#create confusion matrix
conf_matrix <- matrix(c(15, 5, 5, 375), nrow= 2 )

#view confusion matrix
conf_matrix

     [,1] [,2]
[1,] 15 5
[2,] 5,375

#calculate Matthews correlation coefficient for confusion matrix
mcc(confusionM = conf_matrix)

[1] 0.7368421

पुनः, मैथ्यूज सहसंबंध गुणांक 0.7368 है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर में अन्य सामान्य कार्य कैसे करें:

आर में लॉजिस्टिक रिग्रेशन कैसे करें
Ggplot2 का उपयोग करके ROC वक्र कैसे प्लॉट करें
आर में एफ1 स्कोर की गणना कैसे करें