आर में लघुगणक प्रतिगमन (कदम दर कदम)

लॉगरिदमिक रिग्रेशन एक प्रकार का रिग्रेशन है जिसका उपयोग उन स्थितियों को मॉडल करने के लिए किया जाता है जिनमें वृद्धि या गिरावट पहले तेजी से बढ़ती है और फिर समय के साथ धीमी हो जाती है।

उदाहरण के लिए, निम्नलिखित ग्राफ लघुगणकीय क्षय का एक उदाहरण दिखाता है:

इस प्रकार की स्थिति के लिए, एक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को लॉगरिदमिक प्रतिगमन का उपयोग करके अच्छी तरह से तैयार किया जा सकता है।

लघुगणक प्रतिगमन मॉडल के लिए समीकरण निम्नलिखित रूप लेता है:

y = a + b*ln(x)

सोना:

• y: प्रतिक्रिया चर
• x: पूर्वानुमानित चर
• ए, बी: प्रतिगमन गुणांक जो एक्स और वाई के बीच संबंध का वर्णन करते हैं

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि आर में लॉगरिदमिक प्रतिगमन कैसे करें।

चरण 1: डेटा बनाएं

सबसे पहले, आइए दो वेरिएबल्स के लिए नकली डेटा बनाएं: x और y :

 x=1:15

y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5)

चरण 2: डेटा को विज़ुअलाइज़ करें

इसके बाद, आइए x और y के बीच संबंध को देखने के लिए एक त्वरित स्कैटरप्लॉट बनाएं:

 plot(x, y) 

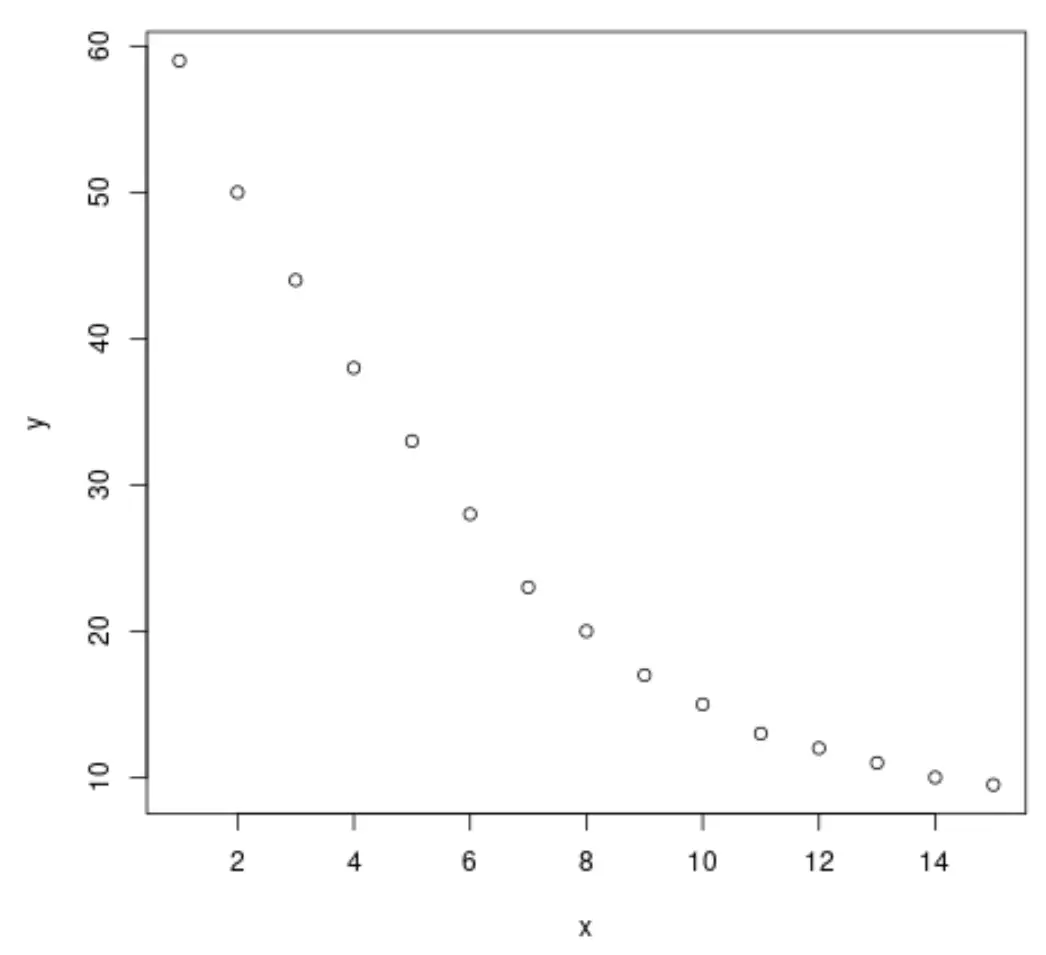
ग्राफ़ से, हम देख सकते हैं कि दो चरों के बीच एक स्पष्ट लघुगणकीय क्षय पैटर्न है। प्रतिक्रिया चर का मान, y , पहले तेजी से घटता है, फिर समय के साथ धीमा हो जाता है।

इसलिए चरों के बीच संबंध का वर्णन करने के लिए लघुगणक प्रतिगमन समीकरण को फिट करना बुद्धिमानी लगता है।

चरण 3: लॉगरिदमिक प्रतिगमन मॉडल को फ़िट करें

इसके बाद, हम लॉगरिदमिक रिग्रेशन मॉडल को फिट करने के लिए एलएम() फ़ंक्शन का उपयोग करेंगे, एक्स के प्राकृतिक लघुगणक को भविष्यवक्ता चर के रूप में और वाई को प्रतिक्रिया चर के रूप में उपयोग करेंगे।

 #fit the model
model <- lm(y ~ log (x))

#view the output of the model
summary(model)

Call:
lm(formula = y ~ log(x))

Residuals:
   Min 1Q Median 3Q Max 
-4.069 -1.313 -0.260 1.127 3.122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.0686 1.4090 44.76 1.25e-15 ***
log(x) -20.1987 0.7019 -28.78 3.70e-13 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.054 on 13 degrees of freedom
Multiple R-squared: 0.9845, Adjusted R-squared: 0.9834 
F-statistic: 828.2 on 1 and 13 DF, p-value: 3.702e-13

मॉडल का समग्र एफ-मूल्य 828.2 है और संबंधित पी-मूल्य बेहद कम (3.702e-13) है, जो दर्शाता है कि मॉडल समग्र रूप से उपयोगी है।

आउटपुट तालिका से गुणांकों का उपयोग करके, हम देख सकते हैं कि फिट लघुगणक प्रतिगमन समीकरण है:

y = 63.0686 – 20.1987 * ln(x)

हम इस समीकरण का उपयोग भविष्यवक्ता चर, x के मान के आधार पर, प्रतिक्रिया चर, y की भविष्यवाणी करने के लिए कर सकते हैं। उदाहरण के लिए, यदि x = 12, तो हम अनुमान लगाएंगे कि y 12.87 होगा:

y = 63.0686 – 20.1987 * ln(12) = 12.87

बोनस: किसी दिए गए भविष्यवक्ता और प्रतिक्रिया चर के लिए लॉगरिदमिक प्रतिगमन समीकरण की स्वचालित रूप से गणना करने के लिए इस ऑनलाइन लॉगरिदमिक रिग्रेशन कैलकुलेटर का उपयोग करने के लिए स्वतंत्र महसूस करें।

चरण 4: लघुगणक प्रतिगमन मॉडल की कल्पना करें

अंत में, हम यह देखने के लिए एक त्वरित ग्राफ़ बना सकते हैं कि लॉगरिदमिक रिग्रेशन मॉडल डेटा में कितनी अच्छी तरह फिट बैठता है:

 #plot x vs. y
plot(x, y)

#define x-values to use for regression line
x=seq(from= 1 , to= 15 , length. out = 1000 )

#use the model to predict the y-values based on the x-values
y=predict(model,newdata=list(x=seq(from= 1 ,to= 15 ,length. out = 1000 )),
          interval=" confidence ")

#add the fitted regression line to the plot (lwd specifies the width of the line)
matlines(x,y, lwd= 2 )

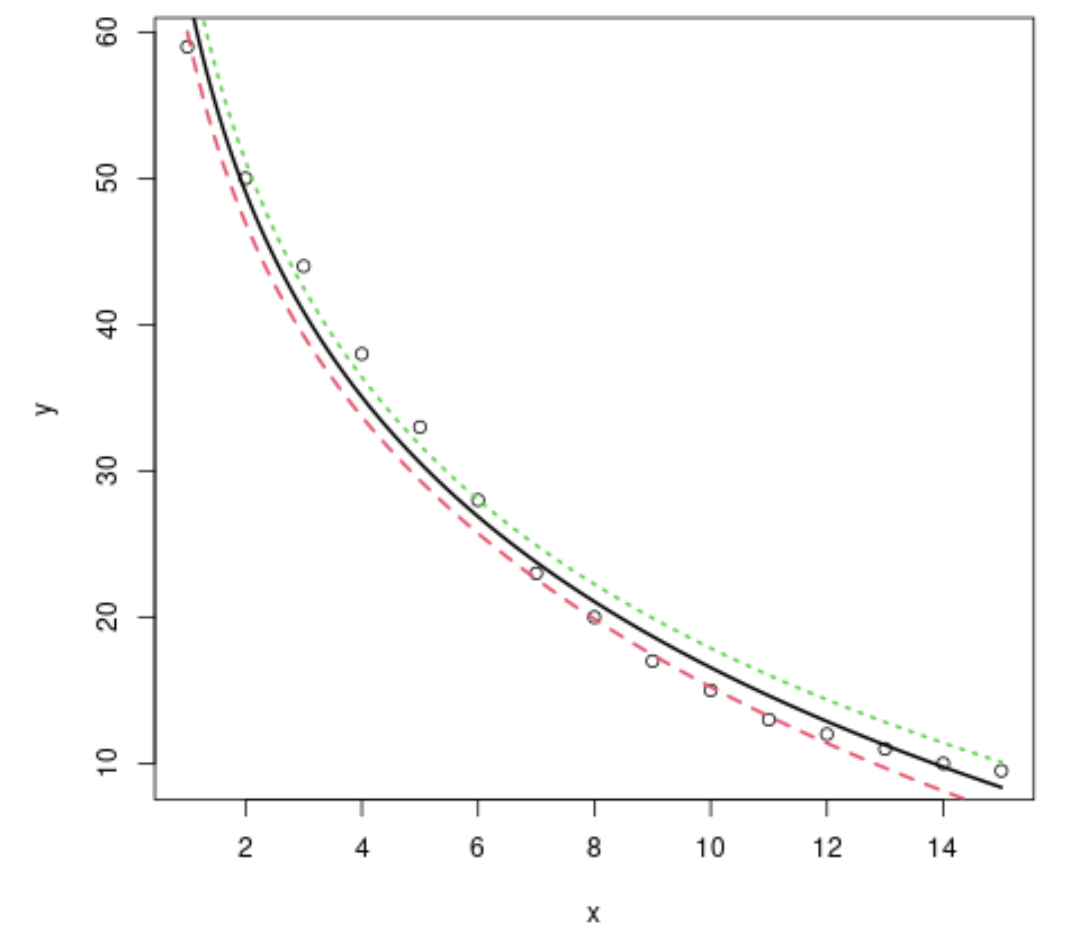
हम देख सकते हैं कि लॉगरिदमिक रिग्रेशन मॉडल इस विशेष डेटा सेट को फिट करने का अच्छा काम करता है।

अतिरिक्त संसाधन

आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में द्विघात प्रतिगमन कैसे करें
आर में घातीय प्रतिगमन कैसे करें
आर में बहुपद प्रतिगमन कैसे करें