आर में लैस्सो रिग्रेशन (कदम दर कदम)

लैस्सो रिग्रेशन एक ऐसी विधि है जिसका उपयोग हम एक रिग्रेशन मॉडल को फिट करने के लिए कर सकते हैं जब डेटा में मल्टीकॉलिनेरिटी मौजूद होती है।

संक्षेप में, न्यूनतम वर्ग प्रतिगमन उन गुणांक अनुमानों को खोजने का प्रयास करता है जो वर्गों के अवशिष्ट योग (आरएसएस) को कम करते हैं:

RSS = Σ(y _i – ŷ _i )2

सोना:

• Σ : एक ग्रीक प्रतीक जिसका अर्थ है योग
• y _i : ^iवें अवलोकन के लिए वास्तविक प्रतिक्रिया मान
• ŷ _i : एकाधिक रेखीय प्रतिगमन मॉडल के आधार पर अनुमानित प्रतिक्रिया मूल्य

इसके विपरीत, लैस्सो प्रतिगमन निम्नलिखित को कम करना चाहता है:

आरएसएस + λΣ|β _जे |

जहां j 1 से p भविष्यवक्ता चर और λ ≥ 0 तक जाता है।

समीकरण में इस दूसरे पद को निकासी दंड के रूप में जाना जाता है। लैस्सो रिग्रेशन में, हम λ के लिए एक मान का चयन करते हैं जो न्यूनतम संभव एमएसई (माध्य वर्ग त्रुटि) परीक्षण उत्पन्न करता है।

यह ट्यूटोरियल आर में लैस्सो रिग्रेशन कैसे करें इसका चरण-दर-चरण उदाहरण प्रदान करता है।

चरण 1: डेटा लोड करें

इस उदाहरण के लिए, हम R के अंतर्निहित डेटासेट का उपयोग करेंगे जिसे mtcars कहा जाता है। हम एचपी को प्रतिक्रिया चर के रूप में और निम्नलिखित चर को भविष्यवक्ता के रूप में उपयोग करेंगे:

• एमपीजी
• वज़न
• मल
• क्यूसेक

लैस्सो रिग्रेशन करने के लिए, हम glmnet पैकेज से फ़ंक्शंस का उपयोग करेंगे। इस पैकेज के लिए आवश्यक है कि प्रतिक्रिया चर एक वेक्टर हो और भविष्यवक्ता चर का सेट data.matrix वर्ग का हो।

निम्नलिखित कोड दिखाता है कि हमारे डेटा को कैसे परिभाषित किया जाए:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

चरण 2: लैस्सो रिग्रेशन मॉडल को फिट करें

इसके बाद, हम लैस्सो रिग्रेशन मॉडल को फिट करने और alpha=1 निर्दिष्ट करने के लिए glmnet() फ़ंक्शन का उपयोग करेंगे।

ध्यान दें कि अल्फा को 0 के बराबर सेट करना रिज रिग्रेशन का उपयोग करने के बराबर है और अल्फा को 0 और 1 के बीच के मान पर सेट करना एक इलास्टिक नेट का उपयोग करने के बराबर है।  

यह निर्धारित करने के लिए कि लैम्ब्डा के लिए किस मान का उपयोग करना है, हम के-फोल्ड क्रॉस-सत्यापन करेंगे और लैम्ब्डा मान की पहचान करेंगे जो सबसे कम परीक्षण माध्य वर्ग त्रुटि (एमएसई) उत्पन्न करता है।

ध्यान दें कि cv.glmnet() फ़ंक्शन स्वचालित रूप से k = 10 बार का उपयोग करके k-फोल्ड क्रॉस-सत्यापन करता है।

 library (glmnet)

#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 5.616345

#produce plot of test MSE by lambda value
plot(cv_model) 

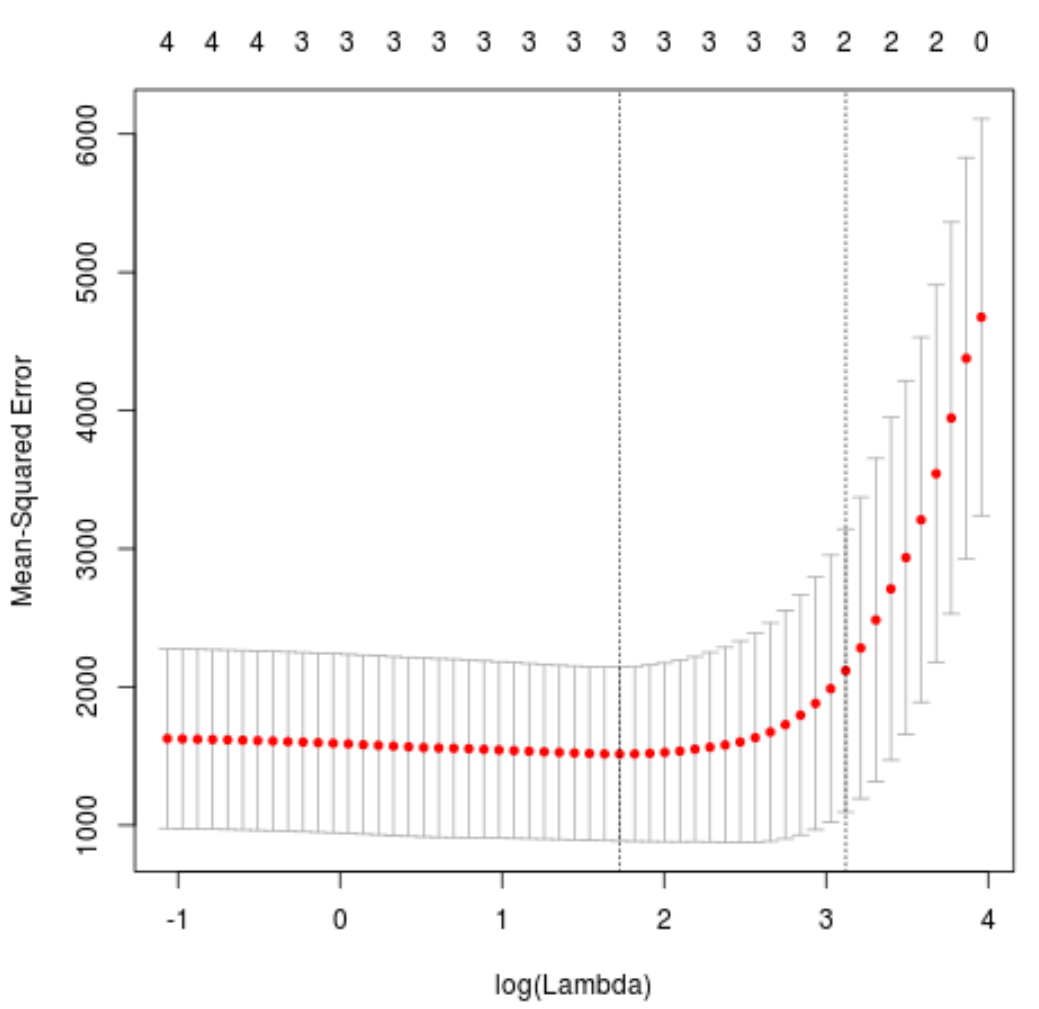
एमएसई परीक्षण को न्यूनतम करने वाला लैम्ब्डा मान 5.616345 निकला।

चरण 3: अंतिम मॉडल का विश्लेषण करें

अंत में, हम इष्टतम लैम्ब्डा मान द्वारा निर्मित अंतिम मॉडल का विश्लेषण कर सकते हैं।

इस मॉडल के लिए गुणांक अनुमान प्राप्त करने के लिए हम निम्नलिखित कोड का उपयोग कर सकते हैं:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.      
qsec -19.43425

ड्रैट प्रेडिक्टर के लिए कोई गुणांक नहीं दिखाया गया है क्योंकि लैस्सो रिग्रेशन ने गुणांक को शून्य तक कम कर दिया है। इसका मतलब यह है कि उन्हें मॉडल से पूरी तरह हटा दिया गया क्योंकि उनके पास पर्याप्त प्रभाव नहीं था।

ध्यान दें कि यह रिज रिग्रेशन और लैस्सो रिग्रेशन के बीच एक महत्वपूर्ण अंतर है। रिज रिग्रेशन सभी गुणांकों को शून्य की ओर कम कर देता है, लेकिन लैस्सो रिग्रेशन में गुणांकों को पूरी तरह से शून्य तक कम करके भविष्यवक्ताओं को मॉडल से हटाने की क्षमता होती है।

हम नई टिप्पणियों के बारे में भविष्यवाणियां करने के लिए अंतिम लैस्सो रिग्रेशन मॉडल का भी उपयोग कर सकते हैं। उदाहरण के लिए, मान लीजिए कि हमारे पास निम्नलिखित विशेषताओं वाली एक नई कार है:

• एमपीजी: 24
• वज़न: 2.5
• कीमत: 3.5
• क्यूसेक: 18.5

निम्नलिखित कोड दिखाता है कि इस नए अवलोकन के एचपी मान की भविष्यवाणी करने के लिए फिट किए गए लैस्सो रिग्रेशन मॉडल का उपयोग कैसे करें:

 #define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 ) 

#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)

[1,] 109.0842

दर्ज किए गए मानों के आधार पर, मॉडल भविष्यवाणी करता है कि इस कार का एचपी मान 109.0842 होगा।

अंत में, हम प्रशिक्षण डेटा पर मॉडल के आर-वर्ग की गणना कर सकते हैं:

 #use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.8047064

R वर्ग 0.8047064 निकला। यानी, सबसे अच्छा मॉडल प्रशिक्षण डेटा के प्रतिक्रिया मूल्यों में 80.47% भिन्नता को समझाने में सक्षम था।

आप इस उदाहरण में प्रयुक्त पूरा आर कोड यहां पा सकते हैं।