आर में सहसंबंध परीक्षण कैसे करें (उदाहरण के साथ)

दो चरों के बीच संबंध को मापने का एक तरीका पियर्सन सहसंबंध गुणांक का उपयोग करना है, जो दो चरों के बीच रैखिक संबंध का एक माप है ।

यह हमेशा -1 और 1 के बीच मान लेता है जहां:

• -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

यह निर्धारित करने के लिए कि सहसंबंध गुणांक सांख्यिकीय रूप से महत्वपूर्ण है या नहीं, आप संबंधित टी-स्कोर और पी-वैल्यू की गणना कर सकते हैं।

सहसंबंध गुणांक (आर) के टी-स्कोर की गणना करने का सूत्र है:

टी = आर * √ एन-2 / √ 1-आर ²

पी-वैल्यू की गणना स्वतंत्रता की एन-2 डिग्री के साथ टी-वितरण के लिए संबंधित दो-पूंछ वाले पी-वैल्यू के रूप में की जाती है।

उदाहरण: आर में सहसंबंध परीक्षण

यह निर्धारित करने के लिए कि क्या दो चर के बीच सहसंबंध गुणांक सांख्यिकीय रूप से महत्वपूर्ण है, आप निम्नलिखित वाक्यविन्यास का उपयोग करके आर में सहसंबंध परीक्षण कर सकते हैं:

cor.test(x, y, विधि=c(“पियर्सन”, “केंडल”, “स्पीयरमैन”))

सोना:

• एक्स, वाई: डिजिटल डेटा वैक्टर।
• विधि: दो वैक्टरों के बीच सहसंबंध की गणना करने के लिए उपयोग की जाने वाली विधि। डिफ़ॉल्ट “पियर्सन” है।

उदाहरण के लिए, मान लीजिए कि हमारे पास R में निम्नलिखित दो वेक्टर हैं:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

दो चरों के बीच सहसंबंध परीक्षण करने से पहले, हम उनके संबंध की कल्पना करने के लिए एक त्वरित स्कैटरप्लॉट बना सकते हैं:

 #create scatterplot
plot(x, y, pch= 16 )

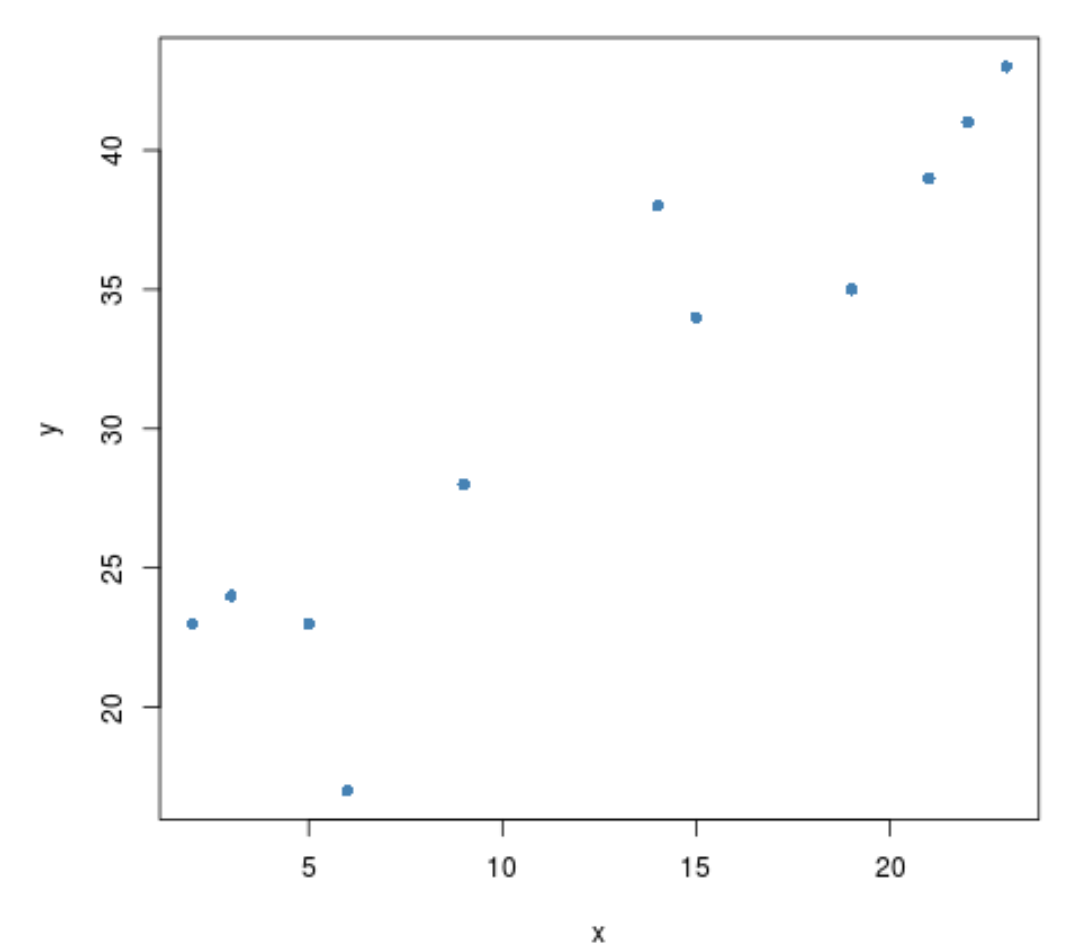
दोनों चरों के बीच एक सकारात्मक सहसंबंध प्रतीत होता है। अर्थात् जैसे-जैसे एक बढ़ता है, दूसरा भी बढ़ता जाता है।

यह देखने के लिए कि क्या यह सहसंबंध सांख्यिकीय रूप से महत्वपूर्ण है, हम एक सहसंबंध परीक्षण कर सकते हैं:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

दोनों सदिशों के बीच सहसंबंध गुणांक 0.9279869 निकला।

परीक्षण आँकड़ा 7.8756 निकला और संगत पी-मान 1.35e-05 है।

चूँकि यह मान 0.05 से कम है, हमारे पास यह कहने के लिए पर्याप्त सबूत हैं कि दोनों चरों के बीच संबंध सांख्यिकीय रूप से महत्वपूर्ण है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल सहसंबंध गुणांक के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

पियर्सन सहसंबंध गुणांक का एक परिचय
“मजबूत” सहसंबंध क्या माना जाता है?
पियर्सन के सहसंबंध की पाँच परिकल्पनाएँ