आर में सामान्यता का परीक्षण कैसे करें (4 तरीके)

कई सांख्यिकीय परीक्षण मानते हैं कि डेटा सेट सामान्य रूप से वितरित होते हैं।

R में इस धारणा की जाँच करने के चार सामान्य तरीके हैं:

1. (दृश्य विधि) एक हिस्टोग्राम बनाएं।

• यदि हिस्टोग्राम लगभग “घंटी” के आकार का है, तो डेटा को सामान्य रूप से वितरित माना जाता है।

2. (दृश्य विधि) एक QQ प्लॉट बनाएं।

• यदि प्लॉट पर बिंदु मोटे तौर पर एक सीधी विकर्ण रेखा के साथ स्थित हैं, तो डेटा को सामान्य रूप से वितरित माना जाता है।

3. (औपचारिक सांख्यिकीय परीक्षण) शापिरो-विल्क परीक्षण करें।

• यदि परीक्षण का पी-मान α = 0.05 से अधिक है, तो डेटा को सामान्य रूप से वितरित माना जाता है।

4. (औपचारिक सांख्यिकीय परीक्षण) कोलमोगोरोव-स्मिरनोव परीक्षण करें।

• यदि परीक्षण का पी-मान α = 0.05 से अधिक है, तो डेटा को सामान्य रूप से वितरित माना जाता है।

निम्नलिखित उदाहरण दिखाते हैं कि व्यवहार में इनमें से प्रत्येक विधि का उपयोग कैसे करें।

विधि 1: एक हिस्टोग्राम बनाएँ

निम्नलिखित कोड दिखाता है कि आर में सामान्य रूप से वितरित और गैर-सामान्य रूप से वितरित डेटासेट के लिए हिस्टोग्राम कैसे बनाया जाए:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

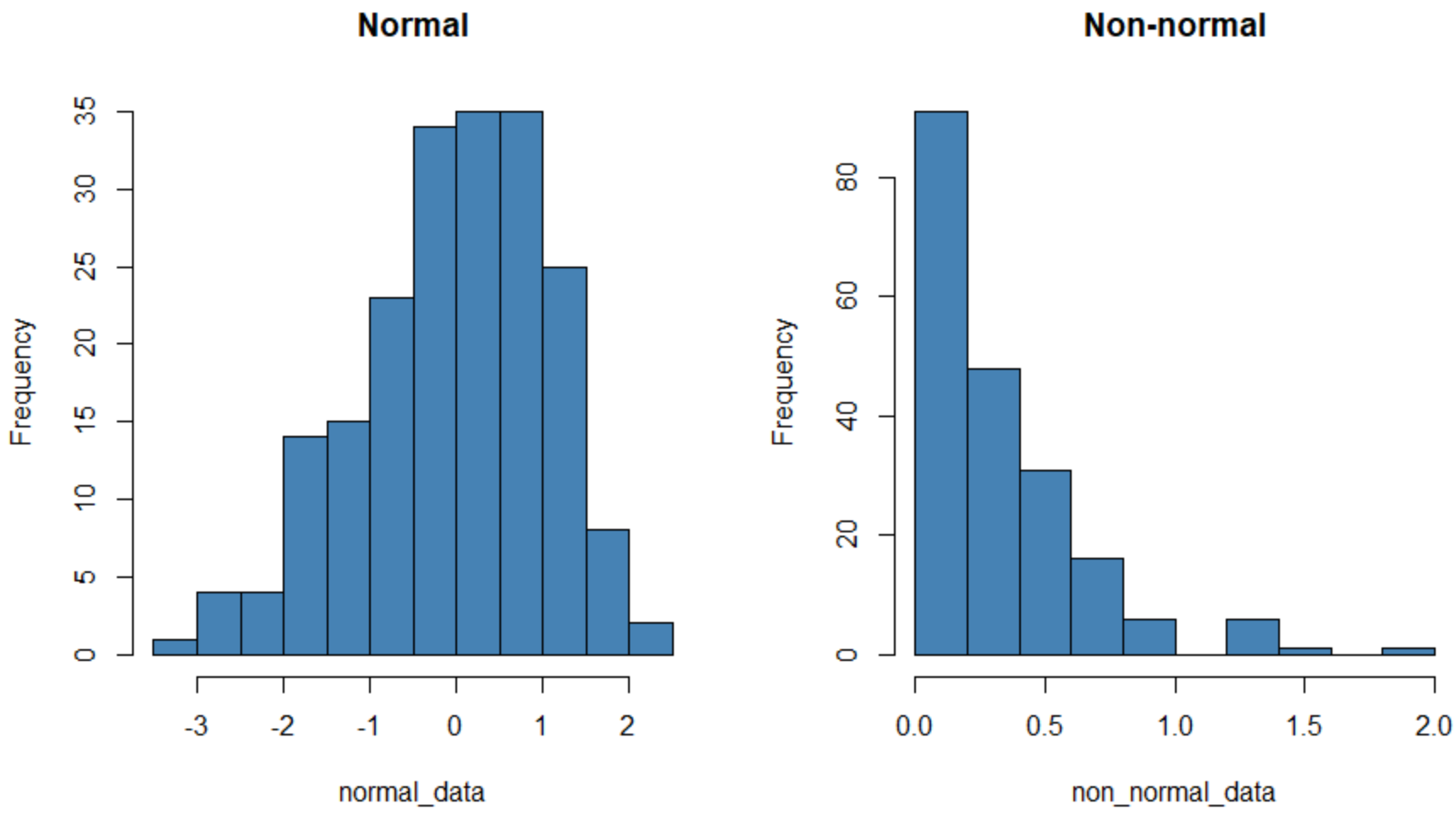
बाईं ओर का हिस्टोग्राम एक डेटा सेट दिखाता है जो सामान्य रूप से वितरित किया जाता है (लगभग “घंटी” के आकार का) और दाईं ओर वाला एक डेटा सेट दिखाता है जो सामान्य रूप से वितरित नहीं होता है।

विधि 2: एक QQ प्लॉट बनाएं

निम्नलिखित कोड दिखाता है कि R में सामान्य रूप से वितरित और गैर-सामान्य रूप से वितरित डेटासेट के लिए QQ प्लॉट कैसे बनाया जाए:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

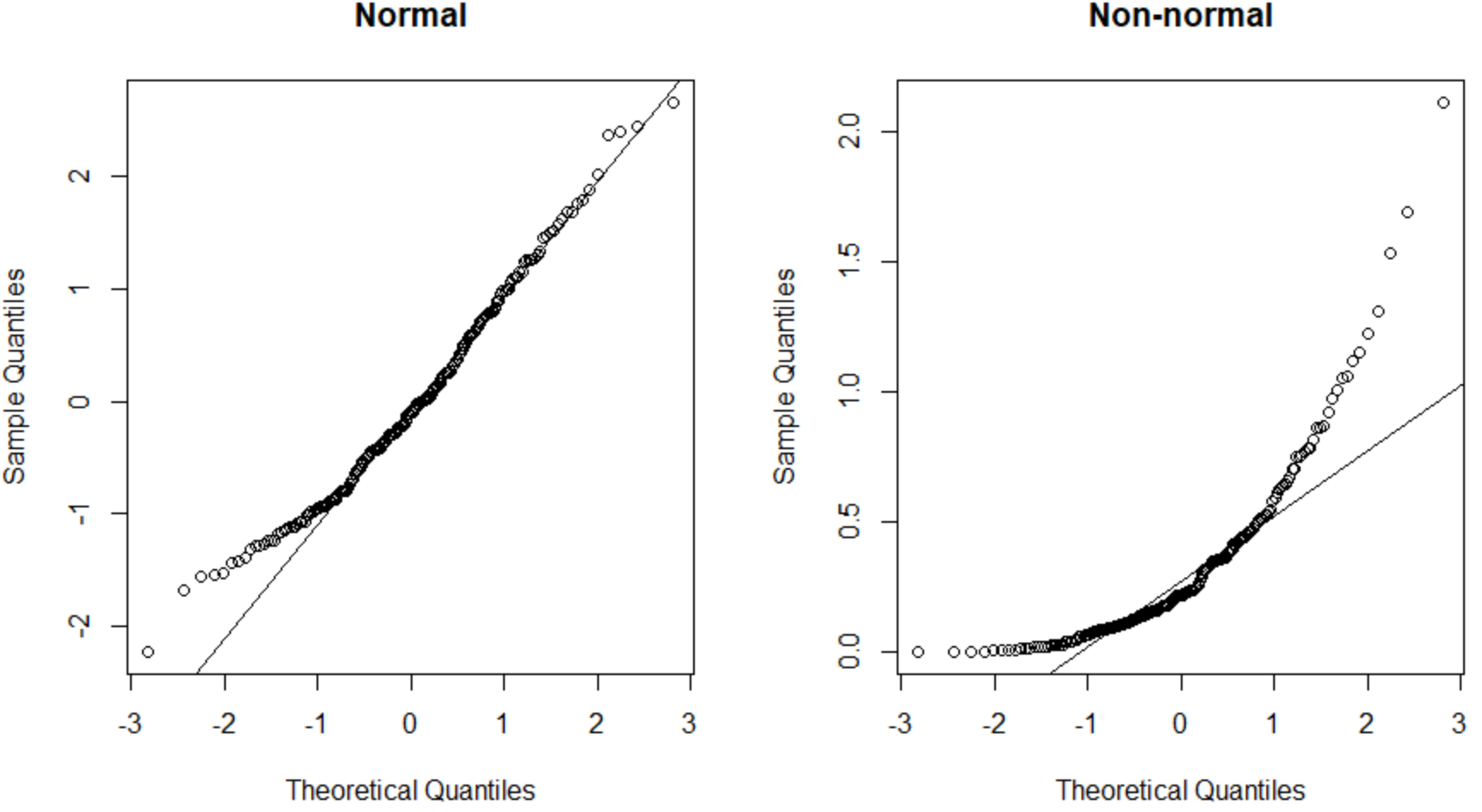
बाईं ओर QQ प्लॉट एक डेटा सेट प्रस्तुत करता है जो सामान्य रूप से वितरित होता है (बिंदु एक सीधी विकर्ण रेखा के साथ आते हैं) और दाईं ओर QQ प्लॉट एक डेटा सेट प्रस्तुत करता है जो सामान्य रूप से वितरित नहीं होता है।

विधि 3: शापिरो-विल्क परीक्षण करें

निम्नलिखित कोड दिखाता है कि आर में सामान्य रूप से वितरित और गैर-सामान्य रूप से वितरित डेटासेट पर शापिरो-विल्क परीक्षण कैसे करें:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

पहले परीक्षण का पी-वैल्यू 0.05 से कम नहीं है, जो इंगित करता है कि डेटा सामान्य रूप से वितरित है।

दूसरे परीक्षण का पी-वैल्यू 0.05 से कम है , जो दर्शाता है कि डेटा सामान्य रूप से वितरित नहीं है।

विधि 4: कोलमोगोरोव-स्मिरनोव परीक्षण करें

निम्नलिखित कोड दिखाता है कि आर में सामान्य रूप से वितरित और गैर-सामान्य रूप से वितरित डेटासेट पर कोलमोगोरोव-स्मिरनोव परीक्षण कैसे करें:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

पहले परीक्षण का पी-वैल्यू 0.05 से कम नहीं है, जो इंगित करता है कि डेटा सामान्य रूप से वितरित है।

दूसरे परीक्षण का पी-वैल्यू 0.05 से कम है , जो दर्शाता है कि डेटा सामान्य रूप से वितरित नहीं है।

गैर-सामान्य डेटा को कैसे प्रबंधित करें

यदि किसी दिए गए डेटा सेट को सामान्य रूप से वितरित नहीं किया जाता है , तो हम इसे अधिक सामान्य रूप से वितरित करने के लिए अक्सर निम्नलिखित परिवर्तनों में से एक कर सकते हैं:

1. लॉग परिवर्तन: x मानों को log(x) में बदलें।

2. वर्गमूल परिवर्तन: x के मानों को √x में बदलें।

3. घनमूल परिवर्तन: x के मानों को x ^1/3 में परिवर्तित करें।

इन परिवर्तनों को निष्पादित करने से, डेटासेट आम तौर पर अधिक सामान्य रूप से वितरित हो जाता है।

आर में ये परिवर्तन कैसे करें यह देखने के लिए इस ट्यूटोरियल को पढ़ें।

अतिरिक्त संसाधन

आर में हिस्टोग्राम कैसे बनाएं
R में QQ प्लॉट कैसे बनाएं और उसकी व्याख्या कैसे करें
आर में शापिरो-विल्क परीक्षण कैसे करें
आर में कोलमोगोरोव-स्मिरनोव परीक्षण कैसे करें