आर में कर्व फिटिंग (उदाहरण के साथ)

अक्सर आप वह समीकरण ढूंढना चाहेंगे जो R के वक्र के लिए सबसे उपयुक्त हो।

निम्नलिखित चरण-दर-चरण उदाहरण बताता है कि पॉली() फ़ंक्शन का उपयोग करके आर में डेटा में कर्व्स को कैसे फिट किया जाए और यह कैसे निर्धारित किया जाए कि कौन सा कर्व डेटा के लिए सबसे उपयुक्त है।

चरण 1: डेटा बनाएं और विज़ुअलाइज़ करें

आइए एक नकली डेटासेट बनाकर शुरुआत करें, फिर डेटा की कल्पना करने के लिए एक स्कैटरप्लॉट बनाएं:

 #create data frame
df <- data. frame (x=1:15,
                 y=c(3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46))

#create a scatterplot of x vs. y
plot(df$x, df$y, pch= 19 , xlab=' x ', ylab=' y ') 

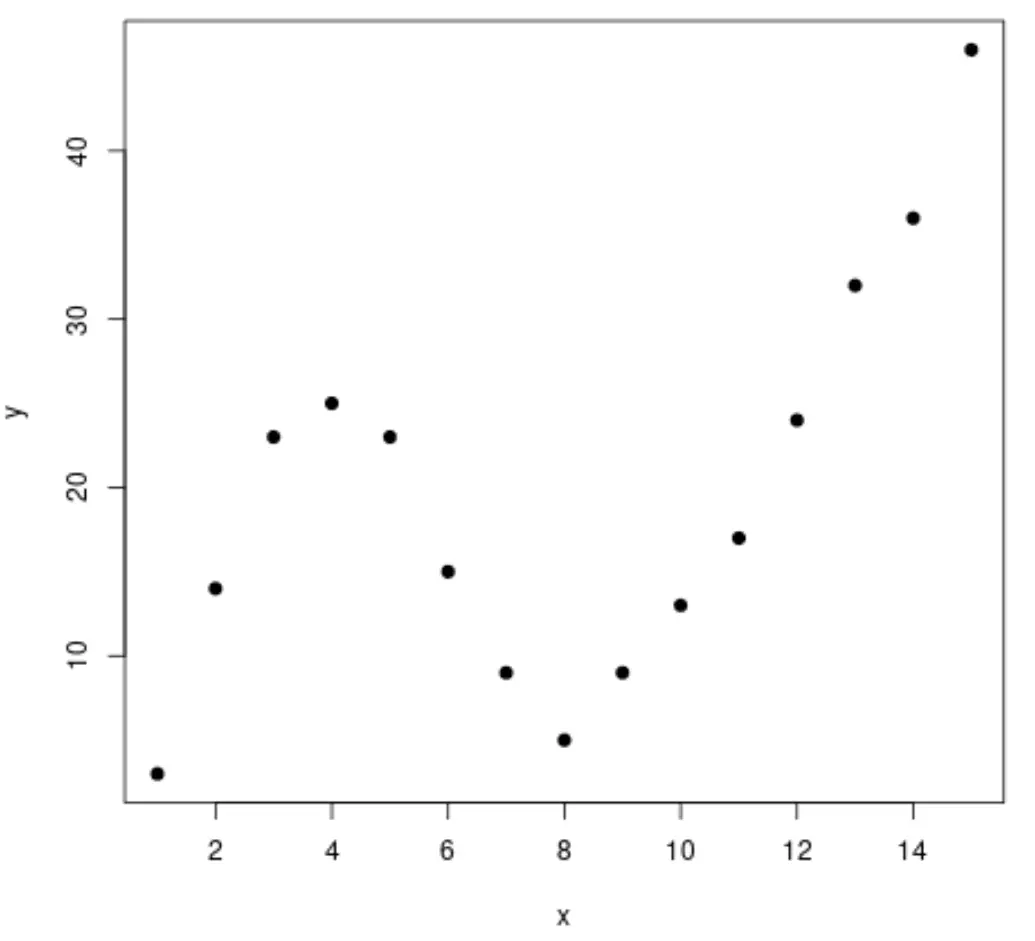
चरण 2: एकाधिक वक्र समायोजित करें

आइए फिर डेटा में कई बहुपद प्रतिगमन मॉडल फिट करें और एक ही प्लॉट में प्रत्येक मॉडल के वक्र की कल्पना करें:

 #fit polynomial regression models up to degree 5
fit1 <- lm(y~x, data=df)
fit2 <- lm(y~poly(x,2,raw= TRUE ), data=df)
fit3 <- lm(y~poly(x,3,raw= TRUE ), data=df)
fit4 <- lm(y~poly(x,4,raw= TRUE ), data=df)
fit5 <- lm(y~poly(x,5,raw= TRUE ), data=df)

#create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of each model to plot
lines(x_axis, predict(fit1, data. frame (x=x_axis)), col=' green ')
lines(x_axis, predict(fit2, data. frame (x=x_axis)), col=' red ')
lines(x_axis, predict(fit3, data. frame (x=x_axis)), col=' purple ')
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')
lines(x_axis, predict(fit5, data. frame (x=x_axis)), col=' orange ')

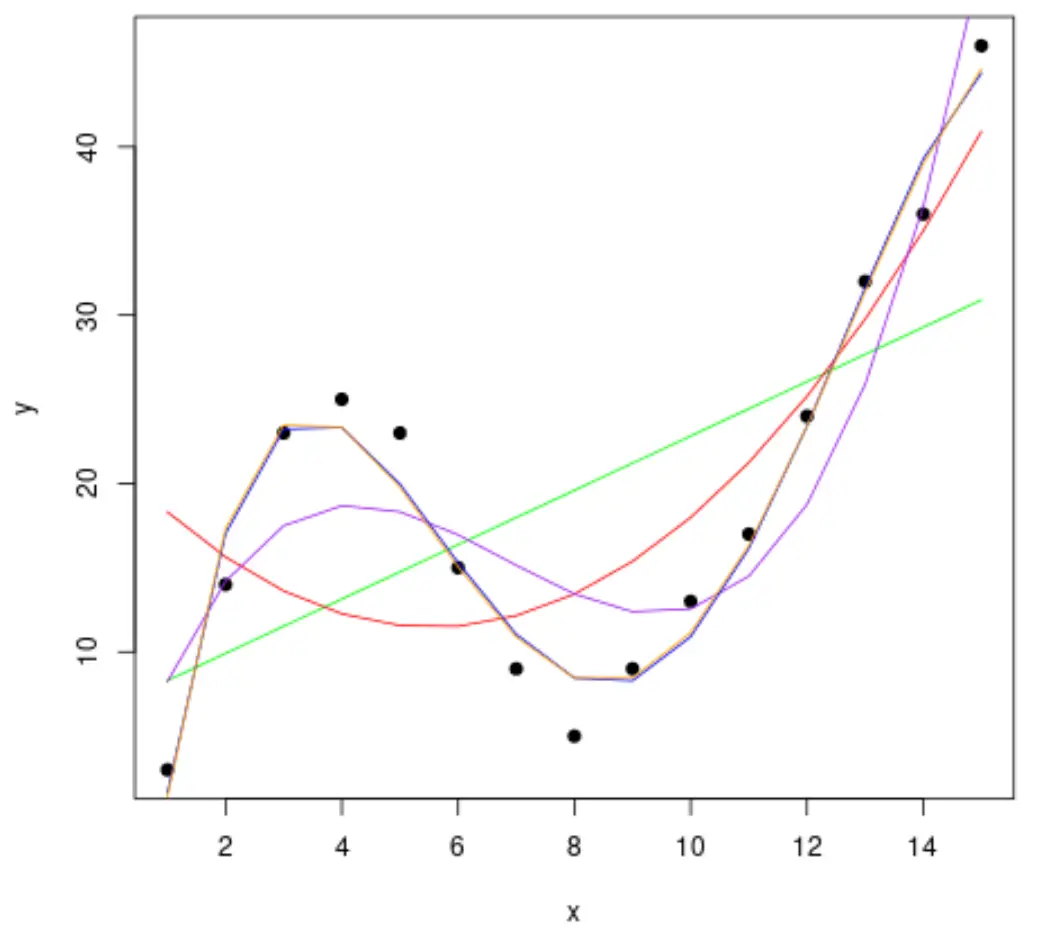
यह निर्धारित करने के लिए कि कौन सा वक्र डेटा के लिए सबसे उपयुक्त है, हम प्रत्येक मॉडल के समायोजित आर वर्ग को देख सकते हैं।

यह मान हमें प्रतिक्रिया चर में भिन्नता का प्रतिशत बताता है जिसे मॉडल में भविष्यवक्ता चर द्वारा समझाया जा सकता है, जिसे भविष्यवक्ता चर की संख्या के लिए समायोजित किया जाता है।

 #calculated adjusted R-squared of each model
summary(fit1)$adj. r . squared
summary(fit2)$adj. r . squared
summary(fit3)$adj. r . squared
summary(fit4)$adj. r . squared
summary(fit5)$adj. r . squared

[1] 0.3144819
[1] 0.5186706
[1] 0.7842864
[1] 0.9590276
[1] 0.9549709

परिणाम से, हम देख सकते हैं कि उच्चतम समायोजित आर-वर्ग वाला मॉडल चौथी डिग्री बहुपद है, जिसका समायोजित आर-वर्ग 0.959 है।

चरण 3: अंतिम वक्र की कल्पना करें

अंत में, हम चौथी डिग्री बहुपद मॉडल के वक्र के साथ एक स्कैटर प्लॉट बना सकते हैं:

 #create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of fourth-degree polynomial model
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')

हम सारांश() फ़ंक्शन का उपयोग करके इस पंक्ति के लिए समीकरण भी प्राप्त कर सकते हैं:

 summary(fit4)

Call:
lm(formula = y ~ poly(x, 4, raw = TRUE), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-3.4490 -1.1732 0.6023 1.4899 3.0351 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) -26.51615 4.94555 -5.362 0.000318 ***
poly(x, 4, raw = TRUE)1 35.82311 3.98204 8.996 4.15e-06 ***
poly(x, 4, raw = TRUE)2 -8.36486 0.96791 -8.642 5.95e-06 ***
poly(x, 4, raw = TRUE)3 0.70812 0.08954 7.908 1.30e-05 ***
poly(x, 4, raw = TRUE)4 -0.01924 0.00278 -6.922 4.08e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.424 on 10 degrees of freedom
Multiple R-squared: 0.9707, Adjusted R-squared: 0.959 
F-statistic: 82.92 on 4 and 10 DF, p-value: 1.257e-07

वक्र का समीकरण इस प्रकार है:

y = -0.0192x ⁴ + 0.7081x ³ – 8.3649x ² + 35.823x – 26.516

हम मॉडल में भविष्यवक्ता चर के आधार पर प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के लिए इस समीकरण का उपयोग कर सकते हैं। उदाहरण के लिए यदि x = 4 है तो हम अनुमान लगाएंगे कि y = 23.34 :

y = -0.0192(4) ⁴ + 0.7081(4) ³ – 8.3649(4) ² + 35.823(4) – 26.516 = 23.34

अतिरिक्त संसाधन

बहुपद प्रतिगमन का एक परिचय
आर में बहुपद प्रतिगमन (चरण दर चरण)
R में seq फ़ंक्शन का उपयोग कैसे करें